Лекція 4 міри центральної тенденції

Центральна тенденція – це кількісне (чисельне) значення ознаки, до якого тяжіє змінна величина. Оскільки поняття «тяжіє» дещо довільне і з математичної точки зору не цілком коректне, має сенс розглянути різні міри центральної тенденції більш докладно.

У психологічних дослідженнях в якості мір центральної тенденції найчастіше використовуються мода, медіана і середнє арифметичне значення.

Мода

Мода (Mo) – кількісне значення досліджуваної ознаки, яке найбільш часто зустрічається у вибірці. Залежно від того, скільки значень ознаки відповідають визначенню моди, розрізняють мономодальні (що мають одну моду), бімодальні (що мають дві моди) і полімодальні розподіли (мають більш ніж дві моди), а також розподіли, що не мають моди (всі значення ознаки зустрічаються приблизно з однаковою частотою). У бімодальному і полімодальних розподілах, в свою чергу, можна визначити найбільшу і найменшу моди.

У тих випадках, коли аналізуються таблиці згрупованих частот досліджуваної ознаки, як правило, визначається модальний клас, тобто той клас розподілу, в який потрапляє найбільша кількість частот (значень ознаки).

Мода не є достатньо суворою мірою центральної тенденції, оскільки вона не враховує характеру розподілу змінних, а значить може використовуватися лише в попередніх висновках і прогнозах. Крім того, необхідно використовувати моду тільки для великих обсягів вибірок, оскільки для малих вона недостатньо інформативна.

Медіана

Медіана (Md) – значення, яке ділить упорядковану множинність даних (ряд ранжування) ознаки, що вивчається навпіл. Медіана – середнє значення рангового ряду. Праворуч і ліворуч від медіани в упорядкованому ряду залишається по однаковій кількості ознак. Наприклад, для вибірки 2, 3,4, 4, 5, 6, 8, 7, 9 медіаною буде значення 5, так як зліва і праворуч від нього залишається по чотири показники. Якщо ряд включає в себе парне число ознак, то медіаною буде середнє, взяте як півсума величин двох центральних значень ряду. Для наступного ряду 0, 1, 1, 2, 3, 4, 5, 5, 6, 7 медіана буде дорівнювати 3,5.

Знання медіани корисне для того, щоб встановити, чи є розподіл окремих значень вивченої ознаки симетричним і наближається до так званого нормального розподілу. Середня і медіана для нормального розподілу зазвичай збігаються або дуже мало відрізняються одна від одної.

Медіана відповідає 50-му процентілю, 5-му децілу або 2-му квартілю в групі даних, тобто Md = P₅₀ = D₅ = Q₂.

Мода і медіана не враховують розкидання даних, і змінні, що лежать осторонь від центру, не впливають на їх величину.

Середнє арифметичне значення

Середнє арифметичне значення, або вибіркове середнє значення як статистичний показник є середньою оцінкою досліджуваної в експерименті психологічної якості та дорівнює сумі змінних, поділених на їх число.

Середнє арифметичне обчислюється за формулою:

Міри мінливості

Міри мінливості показують наскільки результати вимірювання відрізняються один від одного і відповідно від свого арифметичного значення.

Дві вибіркові сукупності можуть мати однакові або близькі між собою середні значення ознаки і в той же час істотно відрізнятися за ступенем варіабельності (варіативності) цієї ознаки.

Наприклад, є дві групи досліджуваних (по 100 чоловік в кожній), у яких досліджується коефіцієнт інтелекту (IQ). Середні значення IQ в тій і іншій групі можуть приблизно збігатися (припустимо, IQ₁ = 102 і IQ₂ = 97), і констатація цього факту дасть нам дуже небагато інформації. У той же час відомо, що індивідуальні значення в першій групі досліджуваних змінюються від 85 до 116, а в другій від 60 до 135. На підставі цього ми можемо сказати, що друга вибірка володіє більшою різноманітністю ознаки в порівнянні з першою.

Для визначення ступеня різноманітності (мінливості) досліджуваного параметра використовуються різні критерії: межі різноманітності, розмах варіацій, середнє і стандартне відхилення, дисперсія, коефіцієнт варіації та ін..

Ліміти (межа) різноманітності – це найменше та найбільше значення серед результатів вимірювання:

_{і ншими словами, межа різноманітності ознаки не вичислюється, а лише констатується. Так, у наведеному вище прикладі lim x1 = 85  116 і lim x2 = 60  135.}

Розмах варіацій ( ) є математична різниця між максимальною і мінімальною величиною ознаки:

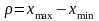
У нашому прикладі розмах варіацій в першій групі ( ₁) складає 116 – 85 = 31 і в другій ( ₂) – 135 – 60 = 75.