Графічне представлення результатів

Графічне представлення результатів психологічного дослідження має ряд безперечних переваг перед табличним (цифровим) матеріалом у тих випадках, коли мова йде про доповіді, наукові звіти і повідомлення, дисертаційні роботи і т. д. Графічне уявлення найбільш наочне, воно дозволяє візуально представити отримані закономірності, зв'язку і ін.

Так при побудові графіка безінтервального варіаційного ряду по осі абсцис (x) відкладають середні значення класів, по осі ординат (y) – частоти. З’єднуючи вершини перпендикулярів прямими лініями, отримують геометричну фігуру у вигляді багатокутника, яка називається полігоном розподілу частот. Лінія поєднуючи вершини перпендикулярів, називається варіаційною кривою або кривою розподілу частот варіаційного ряду.

При побудові графіка інтервального варіаційного ряду по осі абсцис відкладають межі класових інтервалів, а по осі ординат – частоти інтервалів. В результаті отримуємо гістограму розподілу частот.

Якщо по осі абсцис відкладати значення класів, а по осі ординат – накопичені частоти з наступним з’єднанням точок прямими лініями, отримаємо графік, який називається кумулятою. Відкладаючи по осі абсцис частоти, а по осі ординат – значення класів з наступним з єднанням геометричних точок прямими лініями, отримують лінійний графік, який називається огівою.

Визначення квантилів

Квантіль – точка на числовій осі (значення ознаки), що ділить сукупність спостережень у певній пропорції. Визначення квантілів досить часто використовується в психодіагностичних процедурах (при визначенні тестових норм і т. д.). Для визначення квантілів необхідно мати ряд значень досліджуваної ознаки, проранжованих у порядку зростання величини.

Розрізняють декілька різновидів квантілів:

а) квартілі (Q) ділять сукупність спостережень (ранжируваних ряд) на 4 рівні частини: 1-й квартіль (Q1) ділить ряд у співвідношенні 25:75%, 2-й (Q2) – у співвідношенні 50:50% і 3-й (Q3) – у співвідношенні 75:25%.

б) квінтілі (K) ділять вибірку на 5 рівних частин: K₁ – у співвідношенні 20:80%, K₂ – 40: 60%, K₃ – 60:40%, K₄ – 80:20%.

в) децілі (D) ділять ранжований ряд на 10 рівних частин: D₁ = 10%, D₂ = 20%, ... D₉ = 90%.

г) нарешті, процентілі (Р) ділять сукупність спостережень на 100 частин (у процентному відношенні).

Співвідношення квантілів можна представити у вигляді такої схеми:

Приклад: на 20 досліджуваних визначався рівень особистісної тривожності (УЛТ) за тестом Спілбергера. При ранжуванні значень ознаки отриманий наступний варіаційний ряд (див. таблицю). Завдання полягає в тому, щоб визначити значення 1-го, 2-го і 3-го квартілей.

№№	1	2	3	4	5		6	7	8	9	10		11	12	13	14	15		16	17	18	19	20
УЛТ	31	32	32	34	36		36	36	37	39	41		42	42	43	44	45		45	45	46	47	48

Q₁ = 36 Q₂ = 41,5 Q₃ 45

Для визначення значень квартілей розбиваємо ранжований ряд на 4 рівні частини (по 5 значень ознаки). 1-й квартіль розташовується між 5-м і 6-м значеннями ряду, обидва з яких відповідають 36. Отже, Q₁ = 36. 2-й квартіль розташований між 10-м значенням, рівним 41, і 11-м, рівним 42. Представляється розумним визначити значення 2-го квартіля як середнє між двома суміжними значеннями (Q₂ = 41,5). Значення 3-го квартіля лежить між 15-м і 16-м значеннями ряду (Q₃ = 45). Точно так само ми можемо визначити значення квінтілей (розбиття рангового ряду на 5 частин по 4 значення ознаки) або децілів (розбиття ряду на 10 рівних частин по 2 значення змінної в кожній).

Визначення процентілів: 22; 20; 4; 8; 10; 12; 18; 6; 12; 9

h – ширина класу (h=5);

n – кількість результатів вимірювання (n=10);

p – той процентіль, який обчислюється і представлений у долях (р=0,77);

L – нижня межа першого класу накопичених частот (L=14) ≥ за величину рn;

– частота накопичена до межі L ( =7);

– частота в тому інтервалі, який містить L ( =1).

g = 1 + 3,3 lg 10= 1 + 3,3 ×1= 4,3 ≈ 4

класи	Wi	рознесення	fi	Ʃfi
4 – 9	6,5	ǀǀǀ'	3,5	3,5
9 – 14	11,5	'ǀǀǀ	3,5	7
14 – 19	16,5	ǀ	1	8
19 – 24	21,5	ǀǀ	2	10

Приклад: 17; 15; 19; 22; 25; 20; 24; 19; 17, 24

g = 1 + 3,3 lg 10= 1 + 3,3 ×1= 4,3 ≈ 4

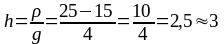
класи	Wi	рознесення	fi	Ʃfi
15 – 18	16,5	ǀǀǀ	3	3
18 – 21	19,5	ǀǀǀ	3	6
21 – 24	22,5	ǀ''	2	8
24 – 27	25,5	ǀ''	2	10

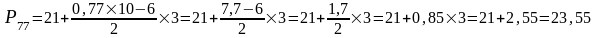Приклад 2:

Х_н – нижня межа класу, який містить процентіль P_i (Х_н=21); вона визначається за величиною К=L_i×n/100, яка більша або рівна в ряді накопичених частот;

λ – ширина класового інтервалу (λ=3);

f_p – частота класу, яка містить процентіль (f_p=2);

Ʃf_i – накопичена частота менша К (Ʃf_i=6)

L_i – порядок проценті ля (L_i=77).