Критерій χr2 Фрідмана

Критерій χ_r² Фрідмана застосовується для співставлення показників, виміряних в трьох або більше умовах на одній і тій же вибірці досліджуваних.

Критерій дозволяє встановити, що величини показників від умови до умови змінюються, але при цьому не вказується напрямок змін.

Даний критерій є поширенням критерію Т Вілкоксона на більшу, ніж 2, кількість умов вимірів. Однак ми ранжуємо не абсолютні величини зсувів, а самі індивідуальні значення, отримані даним досліджуваним в 1,2,3 та наступним вимірах.

Після того, як всі значення будуть проранжовані, підраховуються суми рангів за стовбцями для кожного з проведених вимірів. Якщо відмінності між значеннями ознаки, які отримані в різних умовах, випадкові, то суми рангів за різними умовами будуть приблизно рівні. Але якщо значення ознаки змінюються в різних умовах якимсь закономірним чином, то в одних умовах будуть переважати високі ранги, а в інших – низькі. Суми рангів будуть достовірно відрізнятися між собою. Емпіричне значення критерію χ_r² і вказує на те, наскільки відрізняються суми рангів. Чим більше емпіричне значення χ_r², тим більш суттєві відмінності суми рангів воно відображає.

Якщо χ_r² дорівнює критичному значенню або перебільшує його, відмінності статистично достовірні.

Графіки змін часу вирішення трьох анаграм у п’яти досліджуваних.

Графіки змін ранжованих показників часу вирішення анаграм.

Обмеження критерію:

1. Нижній порог: не менше 2-х досліджуваних (n≥2), кожний з яких пройшов не менше 3-х вимірів (с≥3).

2. При с=3, n≤9, рівень значимості отриманого емпіричного значення χ_r² визначається за таблицею χ_r² Фрідмана (Табл.VII-А); при с=4, n≤4, рівень значимості отриманого емпіричного значення χ_r² визначається за таблицею (Табл. VII-Б); при більших кількостях досліджених або умов отримані емпіричні значення χ_r² зіставляються з критичними значеннями χ², які визначаються за таблицею (Табл. ІХ). це пояснюється тим, що χ_r² має розподіл, схожий з розподілом χ². Число ступенів свободи df визначається за формулою:

df = c – 1

де с – кількість умов вимірів

Приклад: в експерименті з дослідження інтелектуальної наполегливості досліджувані вирішували анаграми, які ускладнювались і вимагали більшого часу на розв’язання. Чи достовірні відмінності у часі вирішення досліджуваними анаграм?

Н₀: відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, є випадкові.

Н₁: відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, не є випадковими.

Код імені досліджуваного	Анаграма 1: КРУА (РУКА)		Анаграма 2: АЛСТЬ (СТАЛЬ)		Анаграма 3: ИНААМШ (МАШИНА)
1. Л-в	5	1	235	3		7	2
2. П-о	7	1	604	3		20	2
3. К-в	2	1	93	3		5	2
4. Ю-ч	2	1	171	3		8	2
5. Р-о	35	2	141	3		7	1
Суми	51	6	1244	15		47	9
Середні	10,2		248,8			9,4

Загальна сума рангів R=6+15+9=30

Розрахункова формула рангів:

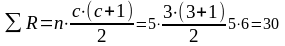
Де n – кількість досліджуваних;

с – кількість умов вимірів.

Визначаємо емпіричне значення χ_r² за формулою:

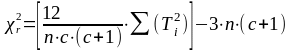
Де с – кількість умов;

n – кількість досліджуваних;

T_i – суми рангів за кожною умовою.

Визначаємо χ_r² для даного випадку:

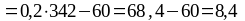
Оскільки в даному прикладі розглядаються три завдання, тобто 3 умови, с=3. Кількість досліджуваних n=5. Це дозволяє нам скористатися спеціальною таблицею χ_r² (Табл. VII-A)

Емпіричне значення χ_r²=8,4 при с=3, n=5 точно відповідає рівню значимості р=0,0085.

Висновок: Н₀ відхиляється. Відмінності в часі, який досліджувані проводять над вирішенням трьох різних анаграм, невипадкові (р=0,0085).

L – критерій Пейджа

Застосовується для співставлення показників, виміряних в трьох та більше умов на одній і тій же вибірці досліджуваних.

Критерій дозволяє виявити тенденції в вимірах величин ознаки при переході від умови до умови. Його можна розглядати як продовження тесту Фрідмана, оскільки він не тільки констатує відмінності, але й вказує на спрямованість змін.

Графіки змін показників часу вирішення анаграм.

L – тест побудований на співставленні сум рангів, а ранжування неминуче округлює отримані показники. Досвід показує, однак, що L – тест є достатньо потужним критерієм, хоч і обмеженим за сферою використання через відсутність таблиць критичних значень для великих n.

Обмеження критерію Пейджа

1. Нижній поріг – 2 досліджуваних, кожний з яких пройшов не менше 3-х вимірів в різних умовах. Верхній поріг – 12 досліджуваних та 6 умов (n≤12, с≤6).

2. Необхідною умовою використання тесту є упорядкованість стовбців даних: зліва повинен розміщуватися стовбець з найменшою ранговою сумою показників, справа – з найбільшою. Можна просто пронумерувати заново всі стовпчики, а потім вести розрахунки не зліва направо, а за номерами, але так легко заплутатися.

Приклад: попередній з анаграмами.

Н₀: Тенденція збільшення індивідуальних показників від першої умови до третьої є випадковою.

Н₁: Тенденція збільшення індивідуальних показників від першої умови до третьої не є випадковою.

Код імені досліджуваного		Умова 1 Анаграма 1				Умова 2 Анаграма 3					Умова 3 Анаграма 2
		час		ранг	час		ранг		час			ранг
1	Л-в		5	1		7		2		235			3
2	П-о		7	1		20		2		604			3
3	К-в		2	1		5		2		93			3
4	Ю-ч		2	1		8		2		171			3
5	Р-о		35	2		7		1		141			3
Суми		51		6	47		9		1244			15
Середні		10,2			9,4				289

Сума рангів складає: 6+9+15=30

Середній час вирішення анаграми 3 навіть менший від анаграми 1. Однак ми досліджуємо не середньо групові тенденції, а ступінь співпадань індивідуальних тенденцій.

Емпіричне значення L визначається за формулою:

L=Ʃ(T_j·j)

Де Т_j – сума рангів за кожною умовою;

j – порядковий номер, приписаний кожній умові в новій послідовності.

L_емп =(6·1)+(9·2)+(15·3)=6+18+45=69

За Табл. VIII визначаємо критичні значення L для даної кількості досліджуваних: n=5, та даної кількості умов: с=3.

L_кр= 66 (р≤0,05)

68 (р≤0,01)

70 (р≤0,001)

Будуємо «вісь значимості»

L_емп ˃ L_кр

Висновок: Н₀ відхиляється. Тенденція збільшення індивідуальних показників від першої умови до третьої не є випадковою. Послідовність анаграм: 1(КРУА), 3(ИНААМШ), 2(АЛСТЬ), - буде більшою мірою відповідати задуму експериментатора про поступове зростання складності завдань, ніж початково використана послідовність.

МАТЕМАТИЧНІ МЕТОДИ В ПСИХОЛОГІЇ: Конспект лекцій навчальної дисципліни для студентів психологічного факультету / Розробники: старший викладач кафедри прикладної психології Нечипоренко О. В.; Черкаський національний університет імені Богдана Хмельницького. – Черкаси: Вид. від. Черкаського національного університету імені Богдана Хмельницького, 2014. – 88 с.

(3,88 друк.арк)

89