Непараметричні міри впливу

G – критерій знаків (Мак-Немара)

Критерій знаків використовується в тих випадках, коли вимір психологічної ознаки проводиться на одній і тій же групі (вибірці) досліджуваних до і після одноразового впливу фактора, який нас цікавить. Він дозволяє встановити, в яку сторону у вибірці в цілому змінюються значення ознаки при переході від першого виміру до другого: чи змінюються показники в сторону підвищення або підсилення, чи навпаки в сторону зниження або послаблення. Критерій знаків застосовується як до зсувів, які можна визначити лише якісно (наприклад, зміни негативного відношення на позитивне), так і до тих зсувів, які можуть бути виміряні кількісно (наприклад, скорочення часу роботи над завданням після експериментального впливу). Критерій знаків досить простий для обчислення і передбачає лише встановлення знака відмінностей між парами порівнюваних величин досліджуваної ознаки до і після впливу. Підсумовуючи число позитивних і негативних зрушень, знаходиться їх співвідношення і порівнюється з табличним (критичним). Вплив фактору вважається статистично достовірним, якщо відмінності значень перевищують табличне значення. Якщо в експериментальних даних є нульові зрушення (тобто досліджувана ознака не змінюється під впливом фактора), то такі результати виключаються з розгляду, а кількість спостережень n зменшується на число нульових зрушень.

Зсуви, які є переважаючими, називаються типовими, а зсуви незначні, одиничні, протилежні – нетиповими. Суть критерію знаків полягає в тому, що він визначає чи можна вважати кількість «типових» зсувів переважаючими. Отже, чим менше «нетипових зсувів», тим більша вірогідність вважати «типові зсуви» переважаючими. Чим менше G_емп, тим більш вірогідно, що зсув в «типовому» напрямку статистично достовірний.

Графічне представлення позитивних і негативних зсувів.

В таблиці критерію знаків для різних n знаходиться критичне значення та порівнюється з емпіричним. Оскільки критерій знаків є одним з трьох виключень з загальних правил,то зона значимості простирається вліво, в сторону більш низьких значень і свідчіть про більшу достовірність «типових» зсувів.

Обмеження критерію знаків:

Кількість спостережень в обох вимірах повинна бути не менше 5 та не більше 300.

Приклад: Визначити, чи є зміна рівня тривожності статистично значущою. Результати вимірювання рівня тривожності до і після проведення тренінгу в групі випробуваних відображені в таблиці.

H₀: переважання типового напрямки зсуву є випадковим.

Н₁: переважання типового напрямки зсуву не є випадковим.

№ досліджуваних	Рівень тривожності «до» тренінгу	Рівень тривожності «після» тренінгу	Зсув
1	30	34	+4
2	39	39	0
3	35	26	–9
4	34	33	–1
5	40	34	–6
6	35	40	+5
7	22	25	+3
8	22	23	+1
9	32	33	+1
10	23	24	+1
11	16	15	–1
12	34	27	–7
13	33	35	+2
14	34	37	+3

Для перевірки нульової гіпотези визначають типовий зсув ("+" або "–") і визначають число (кількість) типових і нетипових зсувів.

У прикладі число позитивних зсувів = 8 перевершує кількість зсувів у негативному напрямку = 5. Тому в даній задачі типовим є позитивне зрушення. З таблиці видно, що число n таких зрушень дорівнює 8.

Емпіричне значення критерію визначається, як число нетипових зрушень. У нашому випадку нетиповий негативний зсув G_емп = 5.

Критичне значення критерію Gкр (α;n) визначають за спеціальною таблицею, де n – загальне число зсувів, тобто обсяг вибірки. n = 13

G_кр = 3 (p≤0,05)

1 (p≤0,01)

Нульова гіпотеза приймається, якщо G_емп ≥ G_кр (α;n).

Оскільки G_емп = 5 > 3 = Gкр (0,05;13), то нульова гіпотеза приймається, і типовий напрямок зсуву є випадковим на обраному рівні значущості.

За відсутності відповідної таблиці, можна скористатися формулою наступного виду:

де N – сума плюсів чи сума мінусів, n – загальне число значень, 0,5 – поправочний коефіцієнт, який додають до N, якщо N < n/2, або віднімають, якщо N > n/2. Критичне значення z (міра Пірсона) для відповідного рівня значущості знаходиться у відповідних таблицях.

Критерій значимості Мак-Немара

Цей критерій застосовується при роботі з номінативними показниками, коли частотні параметри зведені в таблицю крос-табуляції 2x2. Критерій можна використовувати, тільки якщо вихідні дані є пов'язаними вибірками! Формула критерію:

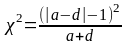
Як вже зазначалося, ступінь свободи для таблиць 2 x 2 завжди дорівнює 1. При порівнянні емпіричних і критичних значень використовується таблиця для критерію «хі - квадрат».

Для ілюстрації обчислень наведена задача. Були опитані 200 відвідувачів магазину побутової техніки. Питання звучало наступним чином: «Чи хочете ви купити кухонний комбайн нової марки?» Опитування проводився два рази. Між першим і другим опитуваннями був показаний ролик, що рекламував цей новий кухонний комбайн. Відповіді були наступні: 10 осіб хотіли зробити покупку і на першому, і на другому етапах, 71 спочатку хотіли купити комбайн, а потім передумали, 74 спочатку не збиралися купувати, а потім вирішили купити, 45 не хотіли і не змінили своєї думки. Відповіді зведені в таблицю (а клітинкам таблиці привласнений літерний код).

до після	+	–
+	a=10	b=71
–	c=74	d=45

Ефективність впливу визначається числом покупців, які змінили свою думку (тобто аналізується різниця між a і b, і між c і d, а всі ці показники, в свою чергу, залежать від N).

Гіпотези:

Н₀: частка покупців, що змінили свою думку з «+» на «–», дорівнює частці покупців, яка змінила думку з «–» на «+».

Н₁: частка покупців, що змінили свою думку з «+» на «–», не дорівнює частці покупців, яка змінила думку з «–» на «+».

При df = 1

x²_кр = 3,841 (р≤0,05)

6,635 (р≤0,01)

Оскільки χ²_емп ˃ χ²_кр нульова гіпотеза відхиляється.

Таким чином, рекламна кампанія була ефективна в психологічному плані. Адже число тих хто змінили думку (71 + 74) виявилося більше числа тих, хто залишилися при своїй думці (10 + 45). А от чи була вона позитивною в плані комерційному? Оскільки число тих хто бажали здійснити покупку до рекламного впливу (10 + 71) ненабагато перевершує число бажаючих купити комбайн після впливу (10 + 74), фінансовий ефект буде невеликий. Кампанія змінює поведінку споживача, але не завжди в потрібному напрямку.

Т – критерій Вілкоксона

Аналогічно критерію знаків, критерій Т Вілкоксона використовується для зіставлення показників, виміряних в двох різних умовах на одній і тій же вибірці досліджуваних. Він дозволяє встановити не тільки спрямованість змін, але і їх вираженість, тобто визначає, чи є зрушення показників в якомусь одному напрямку більш інтенсивним, ніж в іншому. Критерій може бути використаний, якщо досліджувана ознака виміряна в шкалі порядку або шкалі інтервалів. Обсяг вибірки – від 5 до 50 осіб. Нульові зсуви з розгляду виключаються та кількість спостережень n зменшується на кількість цих нульових зсувів.

Пояснити алгоритм розрахунку можна на наступному прикладі. Припустимо, в кабіні літака (і на тренажері) змінили ергономічне середовище. Для виконання певного завдання льотчик раніше витрачав одну кількість секунд, а в новому середовищі він на виконання тих же дій витрачає іншу кількість часу. Таким чином, були зроблені виміри у 10 льотчиків. Визначити достовірність переважання зсуву значень в напрямку однієї зі сторін за умови, що результати другого зрізу обумовлені винятково зміною ергономічного середовища.

Формулюються статистичні гіпотези.

Н₀: переважання зсувів між початковими і кінцевими показниками в одному з напрямків недостовірні (значуще не відрізняються від нуля).

Н₁: переважання зсувів між початковими і кінцевими показниками в одному з напрямків достовірні (значимо відрізняються від нуля).

Визначаються величини зсувів між початковими і кінцевими показниками, потім вони переводяться в абсолютні значення і ранжуються за принципом «меншому значенню – менший ранг». Потім виділяються нетипові (чия спрямованість відрізняється від більшості) ранги і підраховується їх сума. Слід звернути увагу: у нашому прикладі одне із значень d дорівнює 0. Тому при ранжуванні різниць ми присвоюємо йому нульовий ранг.

n	Початкові показники	Підсумкові показники	Різниця показників (d)	Абсолютне значення	Ранг різниці
1	52	51	–1	1	1
2	55	60	+5	5	4,5
3	47	41	–6	6	6,5
4	62	68	+6	6	6,5
5	58	58	0	0	0
6	59	55	–4	4	2,5
7	44	40	–4	4	2,5
8	57	49	–8	8	8
9	61	52	–9	9	9
10	63	68	+5	5	4,5
					45

У таблиці нетипові ранги виділені жирним шрифтом. Сума нетипових рангів дорівнює емпіричному значенню.

T=ƩR_r

Де R_{r –} рангові значення зсувів з більш рідкісним знаком.

Т_емп = 4,5 + 6,5 + 4,5 = 15,5

За таблицею визначаємо значення Т для n=9

Т_кр = 8 (р≤0,05)

3 (р≤0,01)

Для Т-критерію Вілкоксона, що представляє собою виключення із загального правила, принцип прийняття-відхилення нульової гіпотези є наступним: Т_емп < Т_кр => Н₁! Слід додатково додати, що цей критерій може бути одностороннім (якщо напрямок зсувів передбачується) і двостороннім (якщо ми не передбачаємо напрямок зсувів). Рівні значущості для одностороннього та двостороннього критеріїв різні. У нашому випадку ми маємо справу з двостороннім критерієм, бо попередньо не пророкували напрямок відмінностей.

Т_емп > Т_кр (р < 0,05) => Н₀! Ми можемо констатувати, що достовірність переважання зсувів ні в одному з напрямків не встановлена. Можливо, що ми могли б спростувати нульову гіпотезу, якби збільшили кількість спостережень.