Міри впливу Сутність проблеми

У різних галузях психології часто доводиться мати справу з впливом на досліджувану ознаку тих чи інших факторів. Поняття фактора в даному випадку трактується надзвичайно широко: по суті, це будь-який вплив, який може змінювати величину досліджуваної ознаки. Так, в клінічній практиці це може бути дія психотропних препаратів або психотерапевтичного впливу. У педагогічній психології в якості факторів можуть виступати ті чи інші навчально-виховні методики. При дослідженні будь-якої психологічної ознаки в різних вікових групах в якості фактора може розглядатися вік досліджуваних і т. п. При впливі певних факторів або їх сукупності величина досліджуваної ознаки може змінюватися в ту чи іншу сторону. Завдання полягає в тому, щоб на підставі зміни досліджуваної ознаки визначити статистичну достовірність (значимість) впливу даного чинника. Для аналізу достовірності впливу того чи іншого фактора, а також для порівняння між собою сили впливу різних факторів використовуються як параметричні (дисперсійний аналіз), так і непараметричні заходи впливу (G – критерій знаків, критерій Т Вілкоксона та ін.).

Оцінка достовірності зсуву в значеннях досліджуваної ознаки

В психологічних дослідженнях часто буває важливим довести, що в результаті дій якихось факторів відбулися достовірні зміни («зсуви») у вимірюваних показниках.

Багаторазові обстеження одних і тих же осіб протягом тривалого часу є лонгитюдиальне дослідження. Ми можемо створити спеціальні експериментальні умови, які ймовірно впливають на ті чи інші показники і співставити виміри, зроблені до і після експериментального впливу. Якщо зсуви виявляться статистично достовірними, це дозволить нам стверджувати, що експериментальні впливи були суттєвими або ефективними.

Ми можемо зіставляти між собою різні показники одних і тих досліджуваних, якщо вони виміряні в одних і тих же одиницях, за одною і тою шкалою. Наприклад, ми можемо дослідити перепад між вербальним і невербальним інтелектом, виміряними за методикою Векслера, або зіставити експертні оцінки емпатійності та спостережливості, змінені за 10-ти бальною шкалою, або часу вирішення двох завдань, виміряних в секундах, або екзаменаційну успішність за різними дисциплінами.

Для такого роду «перепадів» можна використовувати критерій оцінки достовірності в середніх тенденціях для незалежних вибірок: U-критерій, Q-критерій та кутове перетворення Фішера. Однак перед нами – залежні ряди значень, оскільки вони виміряні на одних і тих же досліджуваних, тому більш обґрунтованим буде використовувати критерії оцінки достовірності зсувів для зв’язаних вибірок. Виключення становлять випадки, коли ми зіставляємо величини зсувів у двох незалежних групах досліджуваних, наприклад експериментальної та контрольної.

Класифікація зсувів та критеріїв оцінки їх статистичної достовірності

Види зсувів	Об’єкт зіставлення	умови		Критерії оцінки достовірності зсуву
		К-ть вимірів	К-ть груп
1. Часові, ситуаційні, мисленєві, вимірювальні	Одні й ті ж показники, виміряні у одних і тих же досліджуваних в різний час, в різних ситуаціях	2	1	G – критерій знаків Т – критерій Вілкоксона
		3 і більше	1	L – критерій тенденцій Пейджа; χ2r – критерій Фрідмана
2. Зсуви під впливом експериментальних впливів	Одні й ті ж показники, виміряні в одних і тих же досліджуваних до та після впливу: а) при відсутності контрольної групи	2	1	G – критерій знаків; Т – критерій Вілкоксона
		3 і більше	1	L – критерій тенденцій Пейджа; χ2r – критерій Фрідмана
	б) за наявності контрольної групи	2	2	Варіант 1 – зіставлення значень «до» і «після» окремо за експер-ною та контрольною групами: G – критерій знаків; Т – критерій Вілкоксона Варіант 2 – зіставлення зсувів у двох групах: Q – критерій U – критерій Манна-Уїтні φ⃰ – критерій Фішера
		3 і більше	2	Зіставлення значень окремо за експер-ною та контрольною групами: L – критерій тенденцій Пейджа; χ2r – критерій Фрідмана
3. Структурні зсуви	Різні показники одних і тих же досліджуваних	2	1	G – критерій знаків; Т – критерій Вілкоксона
		3 і більше	1	L – критерій тенденцій Пейджа; χ2r – критерій Фрідмана

t-критерій Стьюдента для залежних вибірок

t-критерій був розроблений Вільямом Госсетом (1876-1937) для оцінки якості пива на пивоварних заводах Гіннесса в Дубліні (Ірландія). У зв'язку із зобов'язаннями перед компанією з нерозголошення комерційної таємниці (керівництво Гіннесса вважало таким використання статистичного апарату в своїй роботі), стаття Госсета вийшла в 1908 році в журналі «Біометрика» під псевдонімом «Student» (Студент).

Метод Стьюдента для залежних одна від одної вибірок (наприклад, для порівняння результатів, отриманих при повторному тестуванні на одній і тій же вибірці досліджуваних) використовують досить рідко, оскільки для цих цілей існують інші, більш інформативні статистичні прийоми. Проте, для даної мети в першому наближенні можна використовувати формулу Стьюдента такого вигляду:

Отриманий результат порівнюють з табличним значенням для df = n–1 ступенів свободи, де n – число пар значень x і y. Результати порівняння інтерпретуються точно так само, як і у випадку обчислення відмінностей між двома незалежними вибірками.

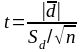
d – середнє арифметичне різниць індивідуальних значень, S_d – стандартне відхилення значень різниць.

Кількість ступенів свободи

df = n – 1

Наступний приклад демонструє алгоритм розрахунку критерію.

Перед початком першого навчального року було виміряно рівень інтелекту у групи студентів. На початку другого навчального року за допомогою паралельної методики знову було виміряно рівень інтелекту. Оскільки можна використовувати результати тільки одних і тих же людей, з подальшої обробки були виключені результати тих студентів, які залишили навчання в інституті (що не піддалися обстеженню на фазі заключних зрізів). Чи можна сказати, що за рік навчання інтелектуальний рівень студентів значно змінився?

1. Формулюються статистичні гіпотези.

Н₀: зсув між показниками початкових і кінцевих зрізів недостовірний.

Н₁: зсув між показниками початкових і кінцевих зрізів достовірний.

2. Обчислюються значення t_емп і df.

df = n–1 = 12–1=11

n	Початковий зріз (xi)	Кінцевий зріз (yi)		di = yi – xi	di – Md		(di – Md)2
1	100	116		16	11		121
2	102	102		0	–5		25
3	105	114		9	4		16
4	120	122		2	–3		9
5	110	119		9	4		16
6	106	116		10	5		25
7	109	100		–9	–14		196
8	115	121		6	1		1
9	115	118		3	–2		4
10	114	124		10	5		25
11	111	119		8	3		9
12	125	121		–4	–9		81
n=12			Ʃdi=60			Ʃ=528

t_кр (p≤0,05)=2,20

(p≤0,01)=3,11

Висновок: емпіричне значення перевищує критичне (при рівні значимості p <0,05 = 2,20), що говорить про наявність достовірних відмінностей між цими вибірками. Отже, нульова гіпотеза про відсутність відмінностей відхиляється.