Критерій φ⃰ - кутового перетворення Фішера
Критерій φ* Фішера призначений для зіставлення двох вибірок за частотою зустрічання даного ефекту, який цікавить дослідника. Він оцінює достовірність відмінностей між процентними частками двох вибірок, в яких зареєстрований ефект, який нас цікавить. Допускається також порівняння процентних співвідношень і в межах однієї вибірки.
Суть кутового перетворення Фішера полягає в переведенні процентних часток в величини центрального кута, який вимірюється в радіанах. Більшій процентній частці відповідатиме більший кут φ, а меншій частці – менший кут, але відносини тут нелінійні:
де Р – процентна доля, виражена в долях одиниці.
Графік залежності кута φ від процентної долі
При збільшенні відмінностей між кутами φ1 і φ2 і збільшенні чисельності вибірок значення критерію зростає. Критерій Фішера обчислюється за такою формулою:
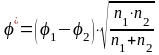
де φ1 – кут, що відповідає більшій процентній долі; φ2 – кут, який відповідає меншій процентній долі; n1 і n2 – відповідно, об’єм першої і другої вибірок.
Приклад 1 – співставлення вибірок за якісно визначеною ознакою
Ми порівнюємо процент досліджуваних в одній вибірці, яка характеризується якоюсь якістю, з процентом досліджуваних в іншій вибірці, яка характеризується тією ж якістю.
Припустимо нас цікавить, чи відрізняються дві групи студентів за успішністю вирішення нової експериментальної задачі. В першій групі з 20 осіб з нею справилися 12 осіб, а в другій вибірці з 25 осіб – 10. В першому випадку процентна доля вирішивши завдання складає
12/20·100%=60%, в другій
10/25·100%=40%
Чи достовірно відрізняються ці процентні долі при даних n1 та n2?
Здається, що «на око» можна визначити, що 60% значно вище 40%. Однак насправді ці відмінності при даних n1 та n2 недостовірні.
Н0: Доля осіб, які справилися з завданням, в першій групі не більша, ніж у другій групі.
Н1: Доля осіб, які справилися з завданням, в першій групі більша, ніж у другій групі.
Побудуємо чотири клітинну таблицю, яка фактично є таблицею емпіричних частот, за двома значеннями ознаки: «є ефект» – «немає ефекту».
Група |
«є ефект» |
«немає ефекту» |
Суми |
1 група |
12 (60%) |
8 (40%) |
20 |
2 група |
10 (40%) |
15 (60%) |
25 |
Суми |
22 |
23 |
45 |
За Табл. ХІІ визначаємо величини φ, які відповідають процентним долям в кожній з груп.
φ1(60%) = 1,772
φ2(40%) = 1,369
Визначаємо емпіричне значення φ* за формулою:
За Табл.ХІІІ визначаємо,якому рівню значимості відповідає φ*емп =1,34:
Р=0,09
Можна встановити і критичні значення φ*, яке відповідає прийнятим в психології рівнем статистичної значимості:
φ*кр = 1,64 (р≤0,05)
2,31 (р≤0,01)
φ*емп =1,34
φ*емп ˂ φ*кр
Будуємо «вісь значимості»
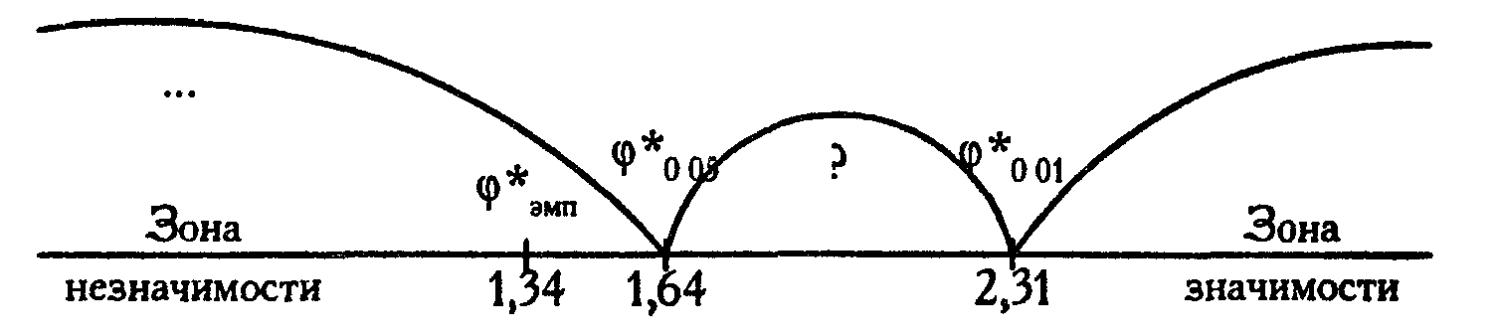
Отримане емпіричне значення φ* знаходиться в зоні не значимості.
Висновок: Н0 приймається. Доля осіб, які справилися з завданням, в першій групі не більша, ніж в другій групі.
Можна лише співчувати дослідникам, які вважають суттєвими відмінності в 20% і навіть 10%, не перевіривши їх достовірність за допомогою критерію φ*. В даному випадку достовірними були б тільки відмінності не менше ніж у 24,3%.