Точковий бісеріальний коефіцієнт кореляції (rpb)

Точковий бісеріальний коефіцієнт кореляції використовується тоді, коли одна змінна формує дихотомічну шкалу найменувань, інша – шкалу інтервалів або шкалу відносин. Порядок обчислень коефіцієнта розглянемо на прикладі наступної задачі.

Умова задачі

У групі досліджуваних, протестованих за тестом Айзенка, виявлено 15 екстравертів, з них 8 з високим рівнем нейротизму (холерики) і 7 – з низьким нейротизмом (сангвініки). Тест Спілбергера виявив у тих і інших наступний рівень особистісної тривожності (УЛТ):

Тип темпераменту	рівень особистісної тривожності
Холерики (1)	42	44	40	38	43	37	41	42	40,9
Сангвініки (0)	34	36	38	40	35	38	39		37,1

Завдання

Визначити рівень зв'язку та її статистичну значущість між типом темпераменту і рівнем особистісної тривожності.

Н₀: кореляція між типом темпераменту та рівнем особистісної тривожності значимо не відрізняється від нуля (є випадковою).

Н₁: кореляція між типом темпераменту та рівнем особистісної тривожності значимо відрізняється від нуля (є невипадковою).

1. Враховуючи, що шкала типів темпераменту дихотомічна, а шкала УЛТ - інтервальна, використовуємо формулу для обчислення точково-бісеріального коефіцієнту кореляції:

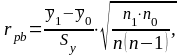
де і , відповідно, середні значення змінних для двох інтервальних шкал, тобто, середні значення УЛТ для холериків ( ) і сангвініків ( );

S_у – стандартне відхилення для всієї вибірки;

n₁ і n₀ – чисельність кожної з порівнювальних вибірок;

n = n₁ + n₀ – загальне число досліджуваних.

2. Визначаємо проміжні значення:

3. _{Проводимо обрахунки:}

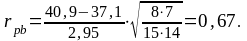
4. Визначаємо число ступенів свободи: ν = (n₁ – 1) + (n₀ – 1) = 7+6=13.

5. Знаходимо критичні значення коефіцієнту кореляції (спеціальної таблиці для r_pb не існує):

r_кр. = 0,441 (р ≤ 0,05) и

0,592 (р ≤ 0,01). r_pb > r_кр..

Кореляція між типом темпераменту і рівнем особистісної тривожності статистично значуща для 1-го і 2-го рівнів.

Статистичну значимість отриманого r_pb оцінюємо за допомогою t-критерію Стьюдента:

Де m_r – помилка коефіцієнта кореляції, r – коефіцієнт кореляції, n – кількість порівнювальних пар.

t_кр= 2,16 р≤0,05

3,01 р≤0,01 t_pb > t_кр..

Висновок: Н₀ відхиляється. Кореляція між типом темпераменту і рівнем особистісної тривожності статистично значуща для 1-го і 2-го рівнів.

Для того, щоб зробити адекватний вибір коефіцієнта кореляції для вирішення тієї чи іншої задачі, необхідно правильно визначити тип шкали, яким представлена та чи інша змінна. Можливі поєднання різних типів шкал і відповідні їм коефіцієнти кореляції представлені в таблиці.

Типи порівнювальних шкал		Коефіцієнт кореляції
1	2
Дихотомічна	Дихотомічна	Дихотомічний (φ)
Дихотомічна	Порядкова (рангова)	Рангово-бісеріальний (rrb)
Дихотомічна	Інтервальна	Точково-бісеріальний (rpb)
Рангова	Рангова	Коефіцієнт Пірсона (rxy) Коефіцієнт Спірмена (rs) Коефіцієнт Кендалла (τ)
Рангова	Інтервальна	Коефіцієнт Пірсона (rxy)
Інтервальна	Інтервальна	Коефіцієнт Пірсона (rxy)

Лекція 9-10