Коефіцієнт рангової кореляції Кендалла (тау Кендалла, t )
Коефіцієнт кореляції Кендалла використовується у випадку, коли змінні представлені двома порядковими шкалами за умови, що пов'язані ранги відсутні. Обчислення коефіцієнта Кендалла пов'язано з підрахунком числа збігів і інверсій. Розглянемо цю процедуру на прикладі попередньої задачі. Алгоритм рішення задачі наступний:
Переоформляємо дані таблиці таким чином, щоб один з рядів (в даному випадку ряд xi ) виявився ранжованим. Іншими словами, ми переставляємо пари x і y в потрібному порядку і вносимо дані в стовпці 1 і 2 таблиці.
xi |
yi |
збіги |
інверсії |
1 |
3 |
9 |
2 |
2 |
6 |
6 |
4 |
3 |
7 |
5 |
4 |
4 |
1 |
8 |
0 |
5 |
2 |
7 |
0 |
6 |
4 |
6 |
0 |
7 |
9 |
3 |
2 |
8 |
5 |
4 |
0 |
9 |
11 |
1 |
2 |
10 |
8 |
2 |
0 |
11 |
12 |
0 |
1 |
12 |
10 |
0 |
0 |
|
Ʃ |
51 |
15 |
Визначаємо «ступінь ранжування» 2-го ряду (yi). Ця процедура проводиться в такій послідовності:
а) беремо перше значення неранжованого ряду «3». Підраховуємо кількість рангів нижче даного числа, які більші за порівнювані значення. Таких значень 9 (числа 6, 7, 4, 9, 5, 11, 8, 12 і 10). Заносимо число 9 в стовпець «збіги». Потім підраховуємо кількість значень, які менші за три. Таких значень 2 (ранги 1 та 2); вносимо число 2 в графу «інверсії».
б) відкидаємо число 3 (ми з ним вже попрацювали) і повторюємо процедуру для наступного значення «6»: число збігів дорівнює 6 (ранги 7, 9, 11, 8, 12 і 10), число інверсій – 4 (ранги 1, 2, 4 і 5). Вносимо число 6 в графу «збіги», а число 4 – в графу «інверсії».
в) аналогічним чином процедура повторюється до кінця ряду; при цьому слід пам'ятати, що кожне «відпрацьоване» значення виключається з подальшого розгляду (підраховуються тільки ранги, які лежать нижче даного числа).
Примітка
Для того щоб не робити помилок у підрахунках, слід мати на увазі, що з кожним «кроком» сума збігів і інверсій зменшується на одиницю; це зрозуміло, якщо врахувати, що кожен раз одне значення виключається з розгляду.
Підраховується сума збігів (Р) і сума інверсій (Q); дані вносяться в одну із трьох взаємозамінних формул коефіцієнта Кендалла (8.10). Проводяться відповідні обчислення.
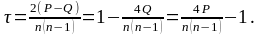
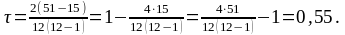
Знаходяться критичні значення коефіцієнта для даної вибірки:
τкр. = 0,45;
0,59.
Емпірично отримане значення порівнюється з табличним.
Висновок
τ = 0,55> τкр. = 0,45. Кореляція статистично значуща для 1-го рівня.
За необхідності (наприклад, при відсутності таблиці критичних значень) статистична значимість τ Кендалла може бути визначена за формулою наступного виду:
де S* = P – Q + 1, якщо P <Q, і
S* = P – Q – 1, якщо P> Q.
S* = P – Q – 1 = 35 і z = 2,40,
Значення z для відповідного рівня значущості відповідають мірі Пірсона і знаходяться за відповідними таблицями. Для стандартних рівнів значимості
Z0,05=1,96
Z0,01=2,58
Z0,001=3,29
Коефіцієнт кореляції Кендалла є статистично значущим, якщо z > zкр
Отже первинний висновок підтверджується: кореляція між ознаками статистично достовірна для 1-го рівня значущості.