Дихотомічний коефіцієнт кореляції (φ)

Коефіцієнт φ використовується в якості міри зв'язку в тих випадках, коли ознаки х і у вимірюються в дихотомічній шкалі найменувань і можуть приймати значення 0 або 1.

Приклад: Проведено соціологічне опитування, яке стосується ставлення населення до релігії. Було опитано 250 респондентів (100 чоловіків і 150 жінок). За результатами опитування виявилося, що серед чоловіків 40 віруючих і 60 атеїстів, а серед жінок 85 виявилися віруючими і 65 - атеїстами.

Визначити, чи існує зв'язок між статтю і ставленням до релігії. Визначити знак і статистичну значущість коефіцієнта кореляції.

Н₀: кореляція між статтю та відношенням до релігії значимо не відрізняється від нуля (є випадковою).

Н₁: кореляція між статтю та відношенням до релігії значимо відрізняється від нуля (є невипадковою).

Введемо необхідні позначення:

- шкала х – стать (1 – чоловіки, 0 – жінки);

- шкала у – ставлення до релігії (1 – віруючий, 0 – атеїст).

Завдання можна вирішити двома різними способами:

1-й спосіб:

Складаємо матрицю співвідношення ознак:

		Ознака х
		1	0	Σ
Ознака у	1	a	b	a + b
	0	с	d	c + d
	Σ	a + c	b + d

			Ознака х
			1		0	Σ
Ознака у	1	40		85		125
	0	60		65		125
	Σ	100		150

Використовуємо формулу дихотомічного коефіцієнту кореляції:

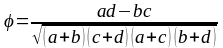
Проводимо обчислення:

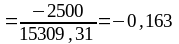
Інтерпретація знаку коефіцієнта кореляції полягає в тому, що якщо він позитивний, то 1 по х корелює з 1 по у, 0 по х корелює з 0 по у. Негативний коефіцієнт (як у нашому випадку) свідчить про те, що 1 по х корелює з 0 по у, 0 по х корелює з 1 по у. Іншими словами, жінки є більш віруючими, а чоловіки - більш атеїстичні. За таблицею критичних значень дихотомічного коефіцієнта кореляції знаходимо, що коефіцієнт є статистично значущим для 1 -го рівня (φ_кр.=0,13).

При відсутності відповідної таблиці можна скористатися наступним співвідношенням (для 1-го рівня значущості):

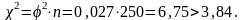
Z_0,05=1,96

Z_0,01=2,58

Z_0,001=3,29

У нашому випадку: z = 2,58 і χ2 = 6,64, тобто висновок підтверджується. Крім того, в Табл. ІХ можна визначити статистичну значимість χ² і для більш високих рівнів (ν=1). Кореляція між статтю і відношенням до релігії є статистично значимою.

Спосіб 2

Коефіцієнт вираховується за формулою:

Р_x – відносна доля досліджуваних, які мають одиницю по х

Р_у – відносна доля досліджуваних,які мають одиницю по у

q_x = 1–P_x які мають нуль по х

q_y = 1–Р_у які мають нуль по у

Р_ху – відносна доля досліджуваних які мають одиниці по х та у

Коефіцієнт φ вираховується за формулою:

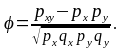
Р_ху=40:250=0,16

Р_х=100:250=0,40

Р_у=125:250=0,50

q_x = 1–P_x =1-0,40=0,60

q_y = 1–Р_у =1-0,50=0,50

Висновок підтверджується.