Класифікації коефіцієнтів кореляції

Коефіцієнти кореляції характеризуються силою і значущістю. Класифікація коефіцієнтів кореляції за силою

Класифікація коефіцієнтів кореляції за силою

Сильна	r˃0,70
Середня	0,50˂r˂069
Помірна	0,30˂r˂0,49
Слабка	0,20˂r˂0,26
Дуже слабка	r˂0,19

Класифікація коефіцієнтів кореляції за значимістю

Високо значима кореляція	r відповідає рівню високої статистичної значимості р≤0,01
Статистично значима кореляція	r відповідає рівню статистичної значимості р≤0,05
Незначима кореляція	r не досягає рівня статистичної значимості р˃0,1

• якщо величина коефіцієнта кореляції між змінними -0,36, то це слабка негативна кореляція, і швидше за все ми не будемо приймати її в розрахунок;

• якщо величина коефіцієнта кореляції дорівнює 0, отже змінні не пов'язані між собою;

• якщо величина коефіцієнта кореляції між змінними дорівнює 0,25 то це дуже слабка кореляція і в більшості випадків ми не беремо її в розрахунок;

• якщо величина коефіцієнта кореляції між змінними дорівнює 0,75 то це висока кореляція і в своїх інтерпретаціях нам варто звернути на неї увагу;

• якщо величина коефіцієнта кореляції дорівнює 1, отже повністю взаємопов'язані.

Не слід плутати ці класифікації, так як вони визначають різні характеристики. Сильна кореляція може виявитися випадковою і, значить, недостовірною. Особливо часто це трапляється у вибірці з малим об'ємом. А у великій вибірці навіть слабка кореляція може виявитися високозначимою.

Визначення значимості кореляції

Після обчислення коефіцієнта кореляції необхідно висунути статистичні гіпотези:

Н₀: показник кореляції значимо не відрізняється від нуля (є випадковим).

H₁: показник кореляції значимо відрізняється від нуля (є невипадковим).

Перевірка гіпотез здійснюється шляхом порівняння отриманих емпіричних коефіцієнтів з табличними критичними. Якщо емпіричне значення досягає критичного рівня або перевищує його, то нульова гіпотеза відхиляється: r_емп˃r_кр відхиляється Н₀, приймаємо Н₁. У таких випадках роблять висновок, що виявлений достовірно значущий зв'язок між показниками.

Якщо емпіричне значення не перевищує критичного, то нульова гіпотеза не відхиляється: r_емп˂r_кр. приймається Н₀. У таких випадках роблять висновок, що не встановлена наявність достовірного зв'язку між показниками.

Лінійна кореляція

Коефіцієнт лінійної кореляції Пірсона (r_xy).

Коефіцієнт кореляції Пірсона називається також коефіцієнтом лінійної кореляції. Він дозволяє визначити силу зв'язку між двома ознаками, виміряними в метричних шкалах.

Вихідний принцип коефіцієнта кореляції Пірсона – використання моментів творення (відхилень значення змінної від середнього значення):

Якщо сума моментів творення велика і позитивна, то х і у зв'язані прямою залежністю; якщо сума велика і негативна, то х і у сильно пов'язані зворотною залежністю; нарешті, у разі відсутності зв'язку між x і у сума добутків моментів близька до нуля.

Для того щоб статистика не залежала від обсягу вибірки, береться не сума добутків моментів, а середнє значення. Однак поділ проводиться не на об’єм вибірки, а на число ступенів свободи n – 1.

Величина є мірою зв’язку між x та y та називається коваріацією x та y.

Для того щоб стандартизувати міру зв'язку, необхідно позбавити коваріацію від впливу стандартних відхилень. Для цього треба розділити S_xy на S_x і S_y:

Послідовність розрахунків можна продемонструвати на наступному прикладі. Отже, необхідно:

Обчислити значення кореляції між показниками росту в сантиметрах і ваги в кілограмах у представників групи студентів.

Поставити питання про достовірність цього коефіцієнта. Для вирішення другого завдання необхідно попередньо сформулювати нульову і альтернативну гіпотези:

Н₀: кореляція між показниками росту та ваги значно не відрізняється від нуля (є випадковою).

Н₁: кореляція між показниками росту та ваги значно відрізняється від нуля (є невипадковою).

Дані заносяться в таблицю, при цьому бажано, щоб один з стовпців значень ознаки (показники зростання або ваги) був впорядкований.

№	xi (ріст)	yi (вага)	xi –M	(xi –M)2	yi –M	(yi –M)2	(xi –M) (yi –M)
1	159	47	-7	49	-11	121	77
2	160	49	-6	36	-9	81	54
3	172	65	6	36	7	49	42
4	160	57	-6	36	-1	1	6
5	171	68	5	25	10	100	50
6	163	50	-3	9	-8	64	24
7	164	59	-2	4	1	1	-2
8	166	68	0	0	10	100	0
9	175	63	9	81	5	25	45
10	170	54	4	16	-4	16	-16
n=10	M=166	M=58		Ʃ=292		Ʃ=558	Ʃ=280

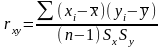
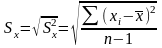
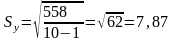
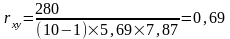
Висновок: можна оцінити зв'язок між показниками росту і ваги як сильну позитивну.

Рівень значимості кореляції

Деякі дослідники, обчисливши значення коефіцієнта кореляції, на цьому і зупиняються. Але з точки зору грамотної методології експерименту слід визначити і рівень значимості (тобто ступінь достовірності) даного коефіцієнта.

Рівень значимості коефіцієнта кореляції обчислюється за допомогою таблиці критичних значень. Якщо отримане в розрахунках значення r_xy перевищує критичне (табличне) значення для даної вибірки, коефіцієнт Пірсона вважається статистично значимим.

Число ступенів свободи в даному випадку відповідає df = n – 2, де n – число пар порівнюваних значень (обсяг вибірки).

r_кр = 0,707 р≤0,05

0,834 р≤0,01

Також рівень значимості можна визначати за коефіцієнтом Стьюдента, який обчислюється як відношення коефіцієнта кореляції до його помилки:

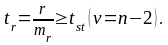
Помилка коефіцієнта кореляції вираховується за формулою:

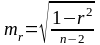
Де m_r – помилка коефіцієнта кореляції, r – коефіцієнт кореляції, n – кількість порівнювальних пар.

У таблиці знаходимо стандартні значення коефіцієнту Стьюдента при числі ступені свободи ν = n – 2 = 8

t_кр= 2,31 р≤0,05

3,36 р≤0,01

Висновок: кореляція між показниками є статистично значимою.

При інтерпретації коефіцієнта кореляції Пірсона необхідно враховувати наступні моменти:

1. Коефіцієнт Пірсона може використовуватися для різних шкал (шкала відносин, інтервальна або порядкова) за винятком дихотомічної шкали.

2. Кореляційний зв'язок далеко не завжди означає зв'язок причинно-наслідковий. Іншими словами, якщо ми знайшли, припустимо, позитивну кореляцію між ростом і вагою у групи досліджуваних, то це зовсім не означає, що ріст залежить від ваги або навпаки (обидві ці ознаки залежать від третьої (зовнішньої) змінної, яка у цьому випадку пов'язана з генетичними конституціональними особливостями людини).

3. r_xy ≈ 0 може спостерігатися не лише при відсутності зв'язку між x і y, а й у разі сильного нелінійного зв'язку (рис. а). У даному випадку негативна і позитивна кореляції врівноважуються і в результаті створюється ілюзія відсутності зв'язку.

4. r_xy може бути досить малий, якщо сильна зв'язок між х і у спостерігається в більш вузькому діапазоні значень, ніж досліджуваний (рис. б).

5. Об'єднання вибірок з різними середніми значеннями може створювати ілюзію досить високою кореляції (рис. в).

. . . . . . . . . . .

. . . . . . . . . . .

. . . . . + + . . + + + + +

Коефіцієнт рангової кореляції Спірмена (r_s)

Обчислення рангової кореляції дозволяє визначити силу і напрямок кореляційного зв'язку між двома ознаками, виміряними в ранговій шкалі або між двома ієрархіями ознак. При цьому по кожній змінній має бути представлено не менше п'яти спостережень. Одним з коефіцієнтів рангової кореляції є коефіцієнт Спірмена.

Коефіцієнт кореляції Спірмена (r_s) використовується в тих випадках, коли обидва ряди змінних представлені ранговими (порядковими) шкалами. Для обчислення коефіцієнта Спірмена можна користуватися двома різними формулами, які дають, в принципі, один і той же результат:

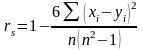
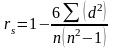
Коефіцієнт кореляції Спірмена, так само як і r_xy, може варіювати від –1 до +1. r_s = 1 тільки в тому випадку, коли ранги обох ознак в точності збігаються за х і у.

Якщо в рядах змінних (або хоча б в одному з них) є пов'язані (повторювані) ранги, то слід користуватися формулою з відповідною поправкою на пов'язані ранги:

де T_x =Ʃ(x³ – x):12;

T_y =Ʃ(y³ – y):12

х – об’єм кожної групи однакових рангів в ранговому ряді х;

y – об’єм кожної групи однакових рангів в ранговому ряді у.

Приклад: у групи студентів були виміряні показники соціального інтелекту (композитна оцінка) за тестом Гілфорда і показники рівня агресивності за тестом Ассінгера. Наскільки можна ставити питання про наявність зв'язку між цими двома особистісними властивостями? Перевірка даних на нормальність розподілу показує, що вони не розподілені за кривою Гаусса. Отже, для їх обробки не можна використовувати аналіз лінійної кореляції. Дані заносяться в таблицю і переводяться з метричних значень в рангові. При цьому висуваються гіпотези:

Н₀: кореляція між показниками соціального інтелекту та рівня агресивності значимо не відрізняється від нуля (є випадковою).

Н₁: кореляція між показниками соціального інтелекту та рівня агресивності значимо відрізняється від нуля (є невипадковою).

Процедура вирахування рангової кореляції Спірмена.

№	Соціальний інтелект		Рівень агресивності		Різниця рангів		Квадрат різниці рангів
	Метричні значення	Ранг	Метричні значення	Ранг
1	55	1	21	8	-7	49
2	52	2	16	11	-9	81
3	49	3	18	10	-7	49
4	46	4	20	9	-5	125
5	42	5	34	6	-1	1
6	39	6	35	5	1	1
7	38	7	38	3	4	16
8	37	8	40	1	7	49
9	35	9	36	4	5	25
10	34	10	14	12	-2	4
11	33	11	29	7	4	16
12	24	12	39	2	10	100
						Ʃd2=416

Підставляючи потрібні значення в формулу, розраховуємо емпіричне значення r_s.

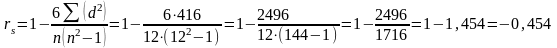
Таким чином, ми приходимо до висновку, що спостерігається помірна негативна кореляція між показниками соціального інтелекту та рівня агресивності. Рівень статистичної значущості r_s при n=12 визначається за таблицею (Табл.ХVI).

r_кр (р≤0,05)=0,58

r_кр (р≤0,01)=0,73

Для даного обсягу вибірки (n=12) мінімальне критичне значення r_s становить 0,58 при р=0,05. Тобто абсолютне значення отриманого результату знаходиться нижче самого мінімального порога статистичної значущості, і ми можемо впевнено прийняти нульову гіпотезу (r_емп<r_кр (р≤0,05)=>Н₀!). Можливо, що для отримання більш достовірних результатів слід було б збільшити об’єм вибірки.

Кореляція між індивідуальними профілями

Приклад: 12 учнів були проранжовані психологом за їх відкритою неприязню до викладача (x_i) і до інших учнів (y_i). Результати експертної оцінки наведені нижче:

№№ дослідж	1	2	3	4	5	6	7	8	9	10	11	12
xi	2	8	12	3	1	6	7	10	4	9	11	5
yi	6	5	10	7	3	4	9	8	1	11	12	2

Завдання. Визначити, чи існує зв'язок між відкритою неприязню учнів до викладача і до інших учнів.

Рішення. Складаємо робочу таблицю для обчислення коефіцієнта кореляції Спірмена і вносимо отримані результати у відповідні формули:

xi	yi	(xi – yi)2	xiyi
2 8 12 3 1 6 7 10 4 9 11 5	6 5 10 7 3 4 9 8 1 11 12 2	16 9 4 16 4 4 4 4 9 4 1 9	12 40 120 21 3 24 63 80 4 99 132 10
	Σ	84	608

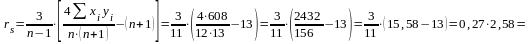
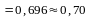
У таблиці критичних значень коефіцієнту кореляції Спірмена знаходимо критичні значення для r_s при n=12: r_кр= 0,58 (р≤0,05)

0,73 (р≤0,01)

Оскільки емпіричне значення більше від критичного значення на рівні р≤0,05, це дає підставу вважати результати статистично достовірними. Зв'язок достовірний, якщо r_{s емп} ≥ r_{s кр0,05} та тим більш достовірний, якщо r_{s емп} ≥ r_{s кр0,01}

Рангова кореляція для пов’язаних рангів

Для оцінки профпридатності на групі професіоналів було складено опис професійно значущих якостей та проведено їх ранжування. З метою прогнозування майбутньої успішності стажера було виконано ранжування ним власних властивостей особистості. Отримані дані були занесені в таблицю. Попередньо були сформульовані нульова і альтернативна гіпотези.

Н₀: відмінності між профілем професіонала і профілем стажиста значимо не відрізняються від нуля.

Н₁: відмінності між профілями значимо відрізняються від нуля.

№	Професійно значимі якості	Профіль професіонала	Профіль стажера	d	d2
1	Працездатність	1	1	0	0
2	Стресостійкість	10	9	1	1
3	Дисциплінованість	7	10	-3	9
4	Вміння згладжувати конфлікти	3	2,5	0,5	0,25
5	Уважність	9	8	1	1
6	Інтелект	7	7	0	0
7	Здоров’я	7	4	3	9
8	Лояльність до фірми	2	2,5	-0,5	0,25
9	Старанність	4,5	6	-1,5	2,25
10	Вміння розбиратися в людях	4,5	5	-0,5	0,25
					Ʃ=23

Як можна бачити з таблиці, в кожному профілі присутні пов'язані ранги. У першому стовпці вони виникли тому що це не індивідуальний, а усереднений профіль. А в другому стовпці – тому що стажист не зміг віддати пріоритет одному з двох якостей (вміння згладжувати конфлікти і лояльність по відношенню до фірми). До речі, цей факт сам по собі може навести психолога на роздуми щодо особистості стажиста, чи порядків, які панують на фірмі. Проте нам необхідно внести поправку на пов'язані ранги:

T_x =Ʃ(x³ – x):12;

T_y =Ʃ(y³ – y):12.

У першому ряду присутні дві групи однакових рангів, складаються з двох і трьох рангів відповідно, отже, х₁ = 2, х₂ = 3.

T_x =[(2³ – 2)+(3³ – 3)]/12=[6+24]/12=30/12=2,5;

В другому ряді присутня одна група однакових рангів, звідси, у=2;

T_y =(2³ – 2)/12=6/12=0,5

Для підрахунку емпіричного значення r_s використовується формула:

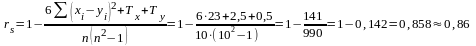
Результат дуже високий, але для остаточного рішення питання про ступінь відповідності першого і другого профілів слід скористатися таблицею критичних значень. З таблиці ми з'ясовуємо, що для отриманого емпіричного значення р≤0,01:

r_кр=0,64 (р≤0,05) та

r_кр=0,79 (р≤0,01). Таким чином, можна зробити висновок, що показник кореляції між профілем професіонала і профілем стажиста високо статистично значущий (не випадковий) і Н₀ відхиляється.