Формулюються статичні гіпотези:
Н0: розподіл уподобань різних напоїв значимо не відрізняється від рівномірного розподілу.
Н1: розподіл уподобань різних напоїв значно відрізняється від рівномірного.
Підраховується загальна кількість виборів.
Pepsi cola |
Coca cola |
Sprite |
Seven Up |
Ʃ |
10 |
14 |
6 |
8 |
38 |
Складення таблиці для вирахування емпіричного значення χ2.
Перший стовпчик (fе) містить значення отриманих при опитуванні емпіричних частот. В другому стовпчику (fТ) містяться значення, які були б отримані, в разі розподілу порівну уподобань. Тобто у всі клітинки заносяться значення, отримані поділом загальної кількості виборів на кількість вибраних напоїв:
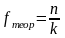
Де n – кількість спостережень; k – кількість розрядів ознаки
Наступний стовпчик містить різницю емпіричної та теоретичної частот. Потім отримані різниці підносяться до квадрату, та діляться на значення теоретичних частот і додаються.
|
fe |
fT |
fe –fT |
(fe –fT)2 |
(fe –fT)2/ fT |
Pepsi cola |
10 |
9,5 |
0,5 |
0,25 |
0,03 |
Coca cola |
14 |
9,5 |
4,5 |
20,25 |
2,13 |
Sprite |
6 |
9,5 |
-3,5 |
12,25 |
1,29 |
Seven Up |
8 |
9,5 |
-1,5 |
2,25 |
0,24 |
|
|
|
|
|
χ2емп=3,68 |
Таким чином, емпіричний показник розраховується за формулою:
Визначається ступінь свободи. Для таблиць такого типу формула має вигляд: df=c–1, де с – це кількість розрядів.
В нашому випадку df=4–1=3.
За допомогою таблиць критичних значень (Табл. ІХ) порівнюємо отримане емпіричне значення з критичним.
df |
p=0,05 |
p=0,01 |
3 |
7,815 |
11,345 |
Будуємо «вісь значимості»
Емпіричний показник (χ2емп=3,68) в рядку df=3 знаходяться лівіше критичного значення 7,815. Це значить, що р-рівень результату знаходиться лівіше рівня тенденції (р=0,05). Таким чином, емпіричне значення нижче критичного при р≤0,05: χ2емп ˂ χ2кр. Таким чином, нам необхідно прийняти нульову гіпотезу, ми констатуємо, що не вдається доказати наявність значимих відмінностей між розподілами уподобань різних напоїв та рівномірним розподілом.
Порівняння емпіричних розподілів.
Під час проведення соціологічного опитування старшокласникам було запропоновано відповісти, якому з трьох можливих напрямків навчання (математичне, природно-наукове або гуманітарне) вони віддадуть перевагу надалі. Серед опитаних були і юнаки і дівчата. Дані зведені в таблицю крос-табуляції. Чи можна сказати, що перевага того чи іншого напряму навчання якось пов'язано з гендерним фактором?
Вихідні дані
|
математика |
Природничі науки |
Гуманітарні науки |
Юнаки |
18 |
10 |
3 |
Дівчата |
10 |
9 |
15 |
Взагалі візуальний аналіз таблиці дозволяє припустити, що юнаки більше бажають спеціальності, пов'язані з математикою, а дівчата - гуманітарні. Але як це довести за допомогою результатів статистичної обробки? Для цього треба порівняти чоловічий і жіночий розподіл переваг напрямків навчання.
До речі, не з усякими зведеними в таблицю даними можна здійснювати подібне порівняння. Вся справа в тому, що для застосування даного критерію є обмеження:
1) загальна сума частот по всім клітинкам повинна бути не менше 30 (n>30);
2) показники теоретичних частот (не емпіричних, а тільки теоретичних!) повинні бути не менше 5 (fT >5). Рішення нашої задачі будується за наступним алгоритмом.