5.4. Типи ексцесу

Теоретично величина ексцесу може варіювати від – 3 до + ∞. Критерій згоди з нормальним розподілом аналогічно коефіцієнту асиметрії визначається за таблицями граничних значень.

Аналогічно визначенню асиметрії розподіл відповідає нормальному (узгоджується з нормальним), якщо Ex < Ex_кр. При зворотному співвідношенні прийнято говорити, що за показником ексцесу емпіричне розподіл статистично достовірно відрізняється від нормального.

Асиметрія та ексцес – дві пов’язані з варіацією властивості форми розподілу. Комплексне їх оцінювання виконується на базі центральних моментів розподілу.

При аналізі емпіричного розподілу може виникнути така ситуація, коли за одним з показників (асиметрії або ексцесу) розподіл відповідає нормальному, за іншим же – відрізняється від нього. У цьому випадку слід використовувати наступне правило: якщо хоча б по одному з вищевказаних показників розподіл достовірно відрізняється від нормального, то слід робити висновок про те, що експериментальний розподіл відрізняється від теоретичного (нормального).

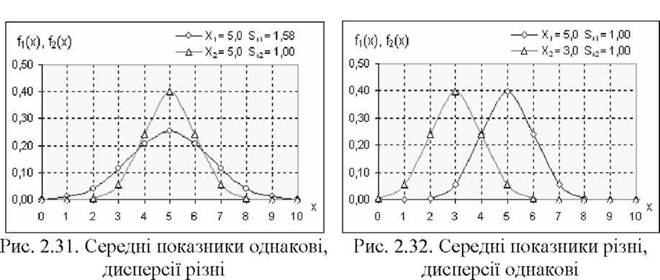
Крім коефіцієнта асиметрії та показника ексцесу, для порівняння експериментального розподілу з теоретичним використовують і інші критерії, зокрема критерій хі-квадрат і критерій λ Колмогорова-Смірнова.

3. Критерій хі-квадрат (χ2) Пірсона

Критерій хі-квадрат заснований на порівнянні між собою емпіричних (експериментальних) частот досліджуваної ознаки і теоретичних частот нормального розподілу. Його називають ще критерієм згоди (емпіричного та теоретичного розподілу).

Використовується у випадках:

• для співставлення емпіричного розподілу ознаки з теоретичним – рівномірним, нормальним або іншим;

• для співставлення двох, трьох або більше емпіричних розподілів однієї і тієї ж ознаки.

Критерій χ² дає відповідь на питання чи з однаковою частотою зустрічаються різні значення ознаки в емпіричному та теоретичному розподілі або в двох та більше емпіричних розподілах.

де f_ei – емпірична частота за і розрядом ознаки;

f_T – теоретична частота;

i – порядковий номер розряду;

k – кількість розрядів ознаки.

Обмеження критерію:

1. Об’єм вибірки повинен бути достатньо великим: n≥30. При n˂30 критерій χ² дає досить наближені значення. Точність критерію збільшується при великих n.

2. Теоретична частота для кожної клітинки таблички не повинна бути менше 5: f≥5. Це значить, що якщо число розрядів задане раніше і не може бути змінене, то ми не можемо використовувати метод χ², не накопичивши відповідного мінімального числа спостережень. Таким чином, якщо кількість розрядів (k) задана раніше, то мінімальне число спостережень (n_min) визначається за формулою: n_min=k·5.

3. Вибрані розряди повинні «вичерпувати» весь розподіл, тобто охоплювати весь діапазон варіативності ознак. При цьому групування на розряди повинна бути однакова у всіх розподілах співставлення.

4. Необхідно вносити «поправку на неперервність» при співставленні розподілів ознак, які набувають всього 2 значення. При внесенні поправки значення χ² зменшується (на 0,5).

(Коли емпіричний розподіл співвідноситься з рівномірним розподілом і кількість розрядів ознаки k=2, а число ступенів свободи ν=k–1=1, тобто ознака набуває всього 2 значення;

коли співставляються два емпіричних розподіли і кількість розрядів рівна 2, тобто кількість рядків k=2, і кількість стовпчиків c=2 і ν=(k–1)·(с–1)=1 необхідно вносити поправку на неперервність)

5. Розряди повинні бути не перехресними: якщо спостереження віднесене до одного розряду, то воно вже не може бути віднесене до іншого розряду. Сума спостережень за розрядами завжди повинна бути рівна загальній кількості спостережень.

Приклад: досліджується питання про уподобання в групі студентів одного з чотирьох напоїв (було запропоновано назвати тільки один улюблений з чотирьох) дані опитування були представлені в таблиці.

Pepsi cola	Coca cola	Sprite	Seven Up
10	14	6	8

Чи можна сказати, що всі напої мають однакове уподобання або що один з них є більш популярним серед студентів. В принципі, з таблиці видно, що кока-кола має самий високий рейтинг, а спрайт самий низький. Але на скільки достовірна ця різниця? Для відповіді на питання потрібно порівняти отриманий емпіричний розподіл з теоретичним рівномірним.

Вирішення задачі будується за наступним алгоритмом.