Расчёт на жёсткость

Деформацию балки (углы поворота поперечных сечений и прогибы) исследуем с помощью универсальных уравнений метода начальных параметров.

С этой целью расчётную схему представим в соответствующем виде (распределённую нагрузку q=20 кН/м продолжим до правого конца балки и тут же «скомпенсируем» её противоположно направленной q=20 кН/м), выбираем единую систему координат с началом в правом конце балки (рис. 4).

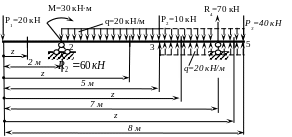
Рис. 4

1. Записываем в общем виде универсальное дифференциальное уравнение изогнутой (упругой) оси балки – одно для всей балки с разделением его по участкам

2. Первое интегрирование дифференциального уравнения даёт уравнение углов поворота поперечных сечений:

3. Интегрирование уравнения углов поворота поперечных сечений даст уравнение прогибов:

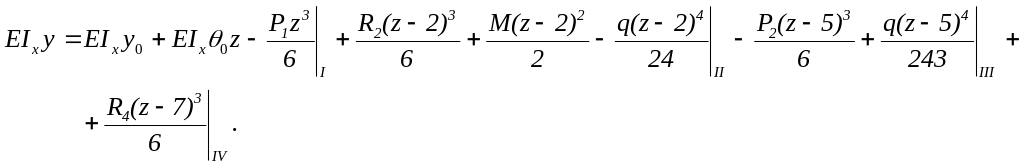
4. Начальные параметры EI_xy₀ и EI_x θ₀ находим из граничных условий (условий закрепления балки):

а) при z=2 м прогиб на опоре 2 равен нулю (конец участка I), т.е.

б) при z=7 м прогиб на опоре 4 равен нулю (конец участка II) т.е.

в) решая систему уравнений

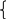
получим: EI_xθ₀=2,5 кН∙м²; EI_xy₀= 21,667 кН∙м³.

5. Универсальные уравнения углов поворота поперечных сечений и прогибов с учётом найденных начальных параметров и значений нагрузки балки примут вид:

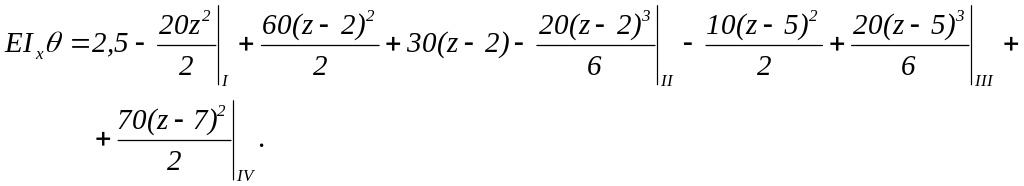
6. Эпюры углов поворота поперечных сечений и прогибов строим по значениям, вычисленным в отдельных сечениях балки с интервалом Δz=1 м. Результаты расчётов сводим в табл. 1.

Таблица 1

Z, м	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0
EIxθ, кН∙м2	2,5	-7,5	-37,5	-30,8	-4,2	22,5	27,5	2,5	-17,5
EIxy, кН∙м3	21,67	20,84	0,0	36,66	55,00	45,00	17,50	0,0	-10,83

Для иллюстрации покажем вычисления для одного из сечений на расстоянии z=6 м (участок III).

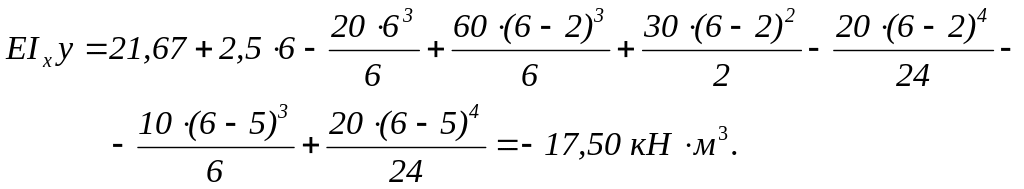
Эпюры EI_xθ и∙EI_xy для удобства анализа полученных результатов изображаем под расчётной схемой на одном рисунке (рис.5).

20

*

*

Эпюра М_и, кН∙м

10

40

40

*

Эпюра EI_xθ, кН∙м²

*

*

*

*

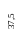
4,12 м

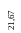
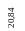
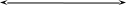
Эпюра EI_xy, кН∙м³

*

*

*

*

*

EI_xy_max=55,28

Рис. 5

На эпюрах EI_xθ и∙EI_xy «звёздочкой» отмечены особые точки – экстремальные значения, точки смены кривизны (точки перегиба). Положение этих точек определяется из дифференциально-интегральных зависимостей между «θ» и «y» и на основании закона Гука при изгибе.

Экстремальное значение прогиба по эпюре EI_xy, (оно же и максимальное по модулю) в сечении на расстоянии z=4,12 м (участок II) (положение сечения определено графически, с учётом принятого масштаба длинны балки).

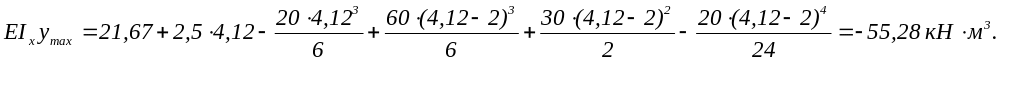7. Для проверки решения определяем угол поворота и прогибов одного из сечений левого сечения балки с помощью интеграла Мора и правила Верещагина.

Символически это принято записывать в виде , т.е. «перемножая» грузовую эпюру изгибающих моментов М_Р=М_и на единичную эпюру изгибающих моментов – от единичного момента (при определении углового перемещения) или от единичной силы (при определении линейного перемещения), приложенных в интересующих сечениях в i-м направлении.

Процедуру перемножения эпюр по правилу Верещагина проиллюстрируем на примере.

7.1. Для «перемножения» грузовую эпюру М_Р=М_и представим расчленённой на простые геометрические фигуры (рис. 6,а), что вообще то следовало бы сделать после построения единичных эпюр (рис. 6,б) и (рис. 6,в), выполняя требование, чтобы в пределах геометрической фигуры единичная эпюра была непрерывной и не имела изломов.

7.2. На единичных эпюрах вычисляем значения y_j под центрами тяжести фигур ω_j расчленённой грузовой эпюры.

Значения y_j проще и надёжнее вычислять не из геометрических соображений, а на основании метода сечений, а это требует определения опорных реакций в единичных состояниях.

Для удобства «перемножения» эпюр значения ω_j и y_j сведём в таблицу

Эпюра Ми	ωj, кН·м2	40	15	45	30	20	40
Эпюра	yj1	1	0,8	0,7	0,6	4/15	2/15
Эпюра	yj2, м	4/3	1,6	1,4	1,2	8/15	4/15

Вычисления всех площадей, кроме ω₃, не требуют пояснений.

На участке 2-3 с равномерно распределённой нагрузкой q=20 кН/м

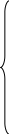
40

ω₃

Эпюра М_и, кН∙м

(в расчленённом виде)

а)

в)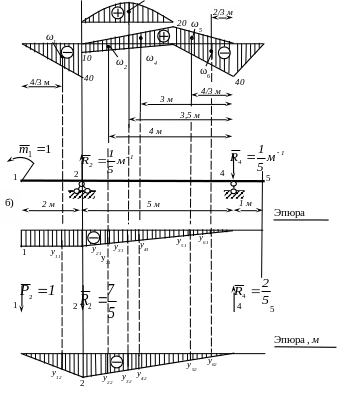

Рис. 6

7.3. Определяем угол поворота и прогиб крайнего левого сечения (т.е. начальные параметры – значения угла поворота сечения и прогиб в начале координат, соответственно

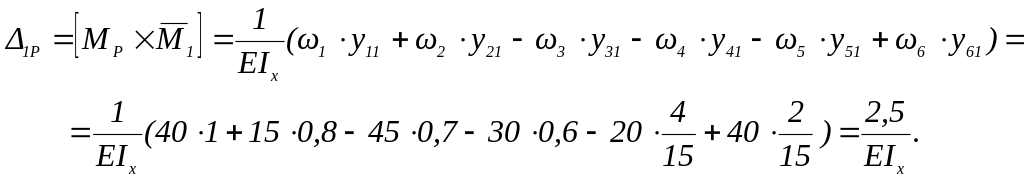
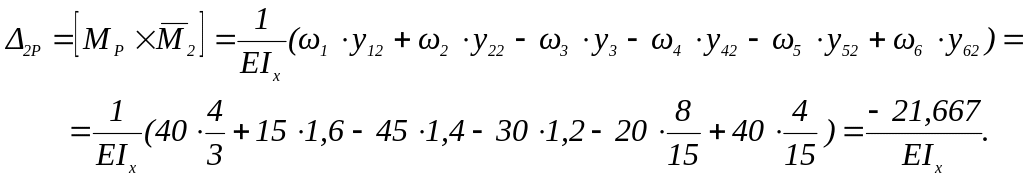
Положительное значение свидетельствует о том, поворот сечения в том же направлении, что и , т.е. против хода часовой стрелки; значение отрицательное, т.е. прогиб направлен вверх – противоположно .

Значения и направления и соответствуют начальным параметрам

θ₀ и у₀ (см. п. 4), что подтверждает правильность решения предыдущего пункта решения с помощью универсального уравнения упругой линии балки.

8. Вычисляем максимальный прогиб балки на участке 2-3

Здесь |EI_xy_max|=55,28 кН·м³=55,28·10⁶ кН·см³; Е=2·10⁵ =2·10⁴ кН/см².

Условие жёсткости выполняется:

Заключение: Окончательно принимаем двутавровое сечение балки № 22, удовлетворяющее условиям прочности и жёсткости.