4.4.1. Статистический анализ модели

Для того чтобы оценки и параметров уравнения регрессии обладали адекватностью ряд остатков 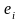должен удовлетворять следующим требованиям:

1. математическое ожидание равно нулю (критерий нулевого среднего);

2. величина является случайной переменной (критерий серий);

3. значения независимы между собой (критерий Дарбина-Уотсона);

4. дисперсия постоянна: 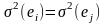для всех i, j (тест Гольдфельда-Квандта);

5. Остатки распределены по нормальному закону (свойство используется для проверки статистической значимости и построения доверительных интервалов при прогнозировании)

Отметим, что аппроксимировать уравнением парной регрессии у на х, имеет смысл только в том случае, если существует достаточно тесная статистическая зависимость между случайными величинами и линейный коэффициент корреляции является значимым, что и имеет место в рассматриваемом примере.

4.4.2. Оценка качества построенной модели

Формально качество модели определяется ее адекватностью и точностью. Эти свойства исследуются на основе анализа ряда остатков (отклонений расчетных значений от фактических):

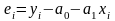(71)

При этом адекватность является более важной составляющей качества, но сначала рассмотрим характеристики точности и нормальности ряда остатков, так как некоторые из них используются при расчете различных критериев адекватности.

Характеристики точности

Под точностью понимается величина случайных ошибок. Сравнительный анализ точности имеет смысл только для адекватных моделей: среди них лучшей признается модель с меньшими значениями характеристик точности, к которым относятся:

- максимальная ошибка 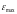соответствует максимальному отклонению расчетных значений от фактических;

- средняя абсолютная ошибка

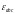
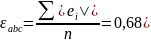
показывает, насколько в среднем отклоняются фактические значения от модели;

- остаточная дисперсия

;

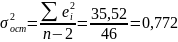- средняя квадратическая ошибка

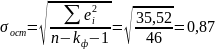(72)

Средняя квадратическая ошибка является наиболее часто используемой характеристикой точности (что объясняется ее связью с остаточной дисперсией, которая играет центральную роль в регрессионном анализе). Значение средней квадратической ошибки всегда несколько больше значения средней абсолютной ошибки, но они имеют схожий смысл – характеризуют среднюю удаленность расчетных значений модели от фактических исходных данных. Обычно точность модели признается удовлетворительной если выполняется условие:

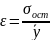*100%= 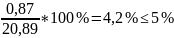(73) К характеристикам точности можно отнести также множественный коэффициент детерминации

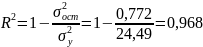, (74) характеризующий долю дисперсии зависимой переменной, объясненной с помощью регрессии, и множественный коэффициент корреляции (индекс корреляции):

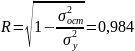(75)

Проверка адекватности модели

Проверка значимости осуществляется на основе t – критерия Стьюдента, т.е. проверяется гипотеза о том, что параметр, измеряющий связь, равен нулю.

Средняя ошибка параметра равна:

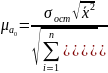, (76)

а для параметра :

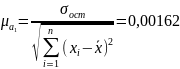. (77)

Расчетные значения t- критерия вычисляются по формуле:

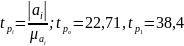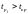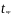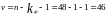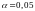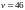
(78) Параметр считается значимым, если . Значение определяется по формуле СТЬЮДЕНТ.ОБР(0,95;46) при числе степеней свободы и с вероятностью (Р=1- ) При и 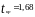. Следовательно, в рассматриваемом примере параметры 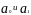являются значимыми.

Параметр 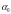лежит в пределах ;( ,

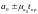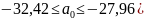а параметр - ; .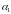

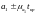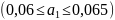Значимость уравнения регрессии в целом определяется с помощью F – критерия Фишера:

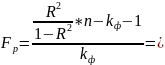279,49 (79)

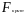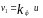
Расчетное значение F сопоставляется с критическим для числа степеней свободы 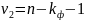при заданном уровне значимости (например, 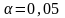), где , .

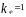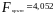Если 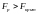, то уравнение считается значимым.

Другой подход к определению значений параметров уравнения парной регрессии и оценке значимости заключается в обращении к режиму “РЕГРЕССИЯ” EXCEL. Следует отметить, что результаты расчётов, приведенные в табл.7-9, получены с меньшими временными затратами и полностью совпадают с результатами “ручного” счёта.

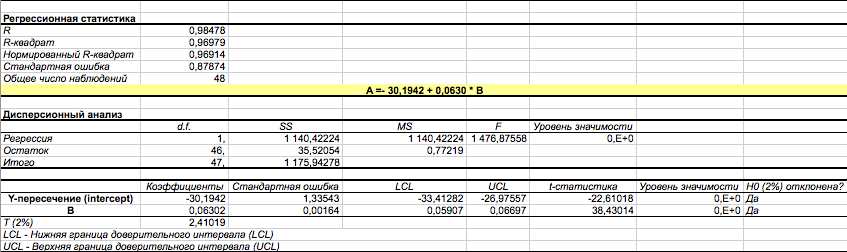
Остатки
Наблюдение	Предсказанное Y	Остаток	Стандартные остатки
1	12,97821	-0,35821	-0,41205
2	13,15971	-0,78971	-0,9084
3	13,2284	-0,4084	-0,46979
4	13,66199	1,80801	2,07975
5	14,62053	1,19947	1,37974
6	14,6407	0,9993	1,14949
7	14,97975	-0,52975	-0,60937
8	15,18772	-1,14772	-1,32022
9	15,21167	-0,84167	-0,96817
10	16,13619	1,98381	2,28197
11	16,65485	0,08515	0,09795
12	17,41425	-0,03425	-0,03939
13	17,58314	-0,06314	-0,07263
14	17,99719	-0,64719	-0,74446
15	18,00412	-0,25412	-0,29232
16	18,5524	0,7976	0,91747
17	18,94439	-1,00439	-1,15535
18	19,19837	0,34163	0,39298
19	19,23492	-1,13492	-1,30549
20	19,39562	0,23438	0,2696
21	19,42461	-0,00461	-0,0053
22	19,74854	0,18146	0,20873
23	19,85441	-0,89441	-1,02884
24	20,6762	-0,9262	-1,06541
25	21,23583	-0,85583	-0,98446
26	21,34738	1,77262	2,03904
27	21,67508	0,64492	0,74184
28	21,83201	0,83799	0,96394
29	22,0488	0,4012	0,4615
30	22,21643	0,21357	0,24566
31	22,5996	-0,7196	-0,82775
32	22,633	-0,673	-0,77415
33	23,03507	-0,82507	-0,94908
34	23,08171	0,05829	0,06705
35	23,49954	-0,95954	-1,10375
36	23,61487	0,37513	0,43152
37	23,95266	0,90734	1,04371
38	24,25327	1,32673	1,52613
39	24,95595	-0,25595	-0,29442
40	25,02275	-0,26275	-0,30224
41	25,1532	0,1068	0,12285
42	26,45206	-0,73206	-0,84209
43	27,45661	-0,32661	-0,3757
44	27,60408	-1,90408	-2,19026
45	27,71311	0,21689	0,24949
46	29,97493	1,49507	1,71978
47	32,09873	0,34127	0,39256
48	32,98543	0,22457	0,25832

Проверка наличия или отсутствия систематической ошибки

1. Проверка свойства нулевого среднего.

Рассчитывается среднее значение ряда остатков:

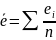. ==-0,0000208 (80)

Если оно близко к нулю, то считается, что модель не содержит систематической ошибки и адекватна по критерию нулевого среднего, иначе – модель неадекватна по данному критерию. Если средняя ошибка не точно равна нулю, то для определения степени ее близости к нулю используется t – критерий Стьюдента. Расчётное значение критерия вычисляется по формуле

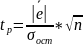(81)

и сравнивается с критическим _. Если выполняется неравенство 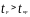, то модель неадекватна по данному критерию.

2. Проверка случайности ряда остатков.

Осуществляется по методу серий. Серией называется последовательность расположенных подряд значений ряда остатков, для которых разность 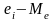(графа 4 табл. 7.4) имеет один и тот же знак, где 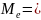-0,020 - медиана ряда остатков, значение которой рассчитано по данным графы 3 упомянутой таблицы

Если модель хорошо отражает исследуемую зависимость, то она часто пересекает линию графика исходных данных и тогда серий много, а их длина невелика. Иначе – серий мало и некоторые из них включают большое число членов.

В качестве серий рассматриваются расположенные подряд ошибки с одинаковыми знаками. Далее подсчитывается число серий 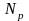и длина максимальной из них 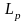. Полученные значения сравниваются с критическими

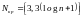(82) 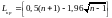(83) (квадратные скобки означают округление вниз до ближайшего целого).

Если выполняется система неравенств:

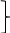
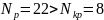
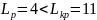(84)

то модель признается адекватной по критерию случайности, если хотя бы одно из неравенств нарушено, то модель признается неадекватной по данному критерию.

3. Проверка независимости последовательных остатков.

Является важнейшим критерием адекватности модели и осуществляется с помощью коэффициента Дарбина-Уотсона:

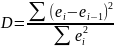=1,66 (85)

Для рядов с тесной взаимосвязью между последовательными значениями остатков значение 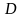близко к нулю, что свидетельствует о том, что закономерная составляющая не полностью отражена в модели и частично закономерность присуща ряду остатков, т.е. модель неадекватна исходному процессу.

Если последовательные остатки независимы, то близко к 2. Это свидетельствует о хорошем качестве модели и чистой фильтрации закономерной составляющей.

При отрицательной автокорреляции остатков (строго периодичном чередовании их знаков) близко к 4.

Для проверки существенности положительной автокорреляции остатков значение сравнивается с 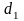и 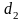из табл. 2 Приложения к лекции:

• если 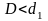, то гипотеза о независимости остатков отвергается и модель признается неадекватной по критерию независимости остатков;

• если 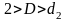, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию (в рассматриваемом примере );

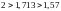• если 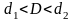, то значение критерия лежит в области неопределенности.

Если 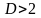, то возникает предположение об отрицательной автокорреляции остатков, и тогда с критическими значениями сравниваются не , а 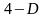и делаются аналогичные выводы.

4. Проверка постоянства дисперсии остатков.

Если на графике остатков они укладываются в симметричную относительно нулевой линии полосу шириной 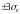(модуль стандартных остатков меньше 3) и не имеют как положительной так и отрицательной тенденций, то дисперсии ошибок наблюдений можно считать постоянными.

Значения стандартных остатков вычисляются по формуле

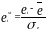, где 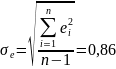и приведены в графе 5 табл.7.4.

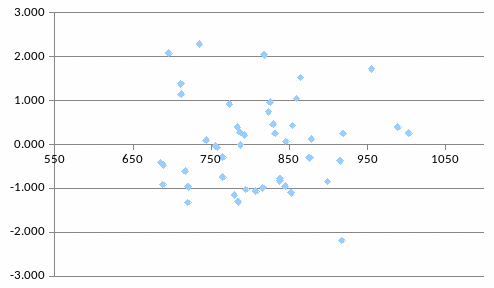
Рис. 7.3 График стандартных остатков

Кроме визуальной оценки постоянства дисперсии существуют и более точные методы, например, тест Гольдфельда-Квандта. Суть теста заключается в следующем. Все n наблюдений упорядочиваются по возрастанию значений независимой переменной (x) и производится оценка параметров регрессий для первых 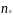и последних наблюдений с помощью метода наименьших квадратов. Для наибольшей мощности теста рекомендуется выбирать значение порядка n/3. Далее вычисляется расчётное значение статистики Фишера

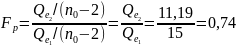, (86)

где 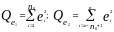- суммы квадратов остатков для первых и последних наблюдений соответственно. Далее задаётся уровень значимости и определяется 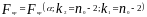с помощъю статистических таблиц. .

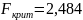Если 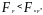то делается вывод о постоянстве дисперсии.

По совокупности четырех критериев делается вывод о принципиальной возможности использования модели: если модель адекватна по критериям постоянства дисперсий и нулевого среднего и хотя бы по одному из двух других критериев, то она может быть принята для использования, хотя и не признается полностью адекватной.