20. Алгоритм построения пересечения двух выпуклых многоугольников. Алгоритм Вейлера-Айзертона пересечения произвольных многоугольников.

Айзертона-Вайдера

Предполагается, что каждый из многоугольников задан списком вершин, причем таким образом, что при движении по списку вершин в порядке их задания внутренняя область многоугольника находится справа от границы.

В случае пересечения границ и отсекаемого многоугольника и окна возникают точки двух типов:

• входные точки, когда ориентированное ребро отсекаемого многоугольника входит в окно,

• выходные точки, когда ребро отсекаемого многоугольника идет с внутренней на внешнюю стороны окна.

Общая схема алгоритма Вейлера-Азертона для определения части отсекаемого многоугольника, попавшей в окно, следующая:

1. Строятся списки вершин отсекаемого многоугольника и окна.

2. Отыскиваются все точки пересечения. При этом расчете касания не считаются пересечением, т.е. когда вершина или ребро отсекаемого многоугольника инцидентна или совпадает со стороной окна.

3. Списки координат вершин отсекаемого многоугольника и окна дополняются новыми вершинами - координатами точек пересечения. Причем если точка пересечения Pk находится на ребре, соединяющем вершины Vi, Vj, то последовательность точек Vi, Vj превращается в последовательность Vi, Pk, Vj. При этом устанавливаются двухсторонние связи между одноименными точками пересечения в списках вершин отсекаемого многоугольника и окна.

Входные и выходные точки пересечения образуют отдельные подсписки входных и выходных точек в списках вершин.

4. Определение части обрабатываемого многоугольника, попавшей в окно выполняется следующим образом:

Если не исчерпан список входных точек пересечения, то выбираем очередную входную точку.

Двигаемся по вершинам отсекаемого многоугольника пока не обнаружится следующая точка пересечения; все пройденные точки, не включая прервавшую просмотр, заносим в результат; используя двухстороннюю связь точек пересечения, переключаемся на просмотр списка вершин окна.

Двигаемся по вершинам окна до обнаружения следующей точки пересечения; все пройденные точки, не включая последнюю, прервавшую просмотр, заносим в результат.

Используя двухстороннюю связь точек пересечения, переключаемся на список вершин обрабатываемого многоугольника.

Эти действия повторяем пока не будет достигнута исходная вершина - очередная часть отсекаемого многоугольника, попавшая в окно, замкнулась. Переходим на выбор следующей входной точки в списке отсекаемого многоугольника.

Модификация этого алгоритма для определения части отсекаемого многоугольника, находящейся вне окна, заключается в следующем:

·исходная точка пересечения берется из списка выходных точек,

·движение по списку вершин окна выполняется в обратном порядке, т.е. так чтобы внутренняя часть отсекателя была слева.

21. Алгоритмы удаления скрытых линий и поверхностей. Алгоритм плавающего горизонта. Алгоритм Робертса.

Плав. горизонта

- Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом х, то текущая кривая видима. В противном случае она невидима.

- Если на участке от предыдущего (x_n) до текущего (x_n+k) значения x видимость кривой изменяется, то вычисляется точка пересечения (x_i).

- Если на участке от x_n до x_n+k сегмент кривой полностью видим, то он изображается целиком; если о он стал невидимым, то изображается фрагмент от x_n до x_i если же он стал видимым, то изображается фрагмент от x_i до x_n+k. Заполнить массивы верхнего и нижнего плавающих горизонтов.

Робертса

Алгоритм прежде всего удаляет из каждого тела те ребра или грани, которые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения того, какая его часть или части, если таковые есть, экранируются этими телами. Поэтому вычислительная трудоемкость алгоритма Робертса растет теоретически, как квадрат числа объектов.

Работа Алгоритм Робертса проходит в два этапа:

1. Определение нелицевых граней для каждого тела отдельно.

Пусть F — некоторая грань многогранника. Плоскость, несущая эту грань, разделяет пространство на два подпространства. Назовем положительным то из них, в которое смотрит внешняя нормаль к грани. Если точка наблюдения – в положительном подпространстве, то грань – лицевая, в противном случае – нелицевая. Если многогранник выпуклый, то удаление всех нелицевых граней полностью решает задачу визуализации с удалением невидимых граней.

Для определения, лежит ли точка в положительном подпространстве, используют проверку знака скалярного произведения (l, n), где l – вектор, направленный к наблюдателю, фактически определяет точку наблюдения; n – вектор внешней нормали грани. Если (l, n) > 0, т. е. угол между векторами острый, то грань является лицевой. Если (l, n) < 0, т. е. угол между векторами тупой, то грань является нелицевой.

В алгоритме Робертса требуется, чтобы все изображаемые тела или объекты были выпуклыми. Невыпуклые тела должны быть разбиты на выпуклые части. В этом алгоритме выпуклое многогранное тело с плоскими гранями должно представиться набором пересекающихся плоскостей. Уравнение произвольной плоскости в трехмерном пространстве имеет вид

aх + by + cz + d = 0

В матричной форме этот результат выглядит так:

[x y z 1][P]^T = 0, где [P]^T = [a b c d] представляет собой плоскость. Поэтому любое выпуклое твердое тело можно выразить матрицей тела, состоящей из коэффициентов уравнений плоскостей, т. е.

где каждый столбец содержит коэффициенты одной плоскости.

Напомним, что любая точка пространства представима в однородных координатах вектором [S] = [х у z 1]. Более того, если точка [S] лежит на плоскости, то [S]·[P]T = 0. Если же [S] не лежит на плоскости, то знак этого скалярного произведения показывает, по какую сторону от плоскости расположена точка. В алгоритме Робертса предполагается, что точки, лежащие внутри тела, дают отрицательное скалярное произведение, т.е. нормали направлены наружу.

2. Удаление невидимых ребер

После первого этапа удаления нелицевых отрезков необходимо выяснить, существуют ли такие отрезки, которые экранируются другими телами в картинке или в сцене. Для этого каждый оставшийся отрезок или ребро нужно сравнить с другими телами сцены или картинки.

Возможны следующие случаи:

- Грань ребра не закрывает. Ребро остается в списке ребер.

- Грань полностью закрывает ребро. Ребро удаляется из списка рассматриваемых ребер.

- Грань частично закрывает ребро. В этом случае ребро разбивается на несколько частей, видимыми из которых являются не более двух. Само ребро удаляется из списка рассматриваемых ребер, но в список проверяемых ребер добавляются те его части, которые данной гранью не закрываются.

Для оптимизации используется приоритетная сортировка (z-сортировка), а также, сравнения с прямоугольными объемлющими оболочками тел. Такой подход позволяет удалить целые группы или кластеры отрезков и тел. Например, если все тела в сцене упорядочены в некотором приоритетном списке, использующем значения z ближайших вершин для представления расстояния до наблюдателя, то никакое тело из этого списка, у которого ближайшая вершина находится дальше от наблюдателя, чем самая удаленная из концевых точек ребра, не может закрывать это ребро. Более того, ни одно из оставшихся тел, прямоугольная оболочка которого расположена полностью справа, слева, над или под ребром, не может экранировать это ребро. Использование этих приемов значительно сокращает число тел, с которыми нужно сравнивать каждый отрезок или ребро.

22. >Алгоритм Варнока. Алгоритм Вейлера-Азертона. (Б)

В пространстве изображения рассматривается окно и решается вопрос о том, пусто ли оно, или его

содержимое достаточно просто для визуализации. Если это не так, то окно разбивается на фрагменты

до тех пор, пока содержимое фрагмента не станет достаточно простым для визуализации или его

размер не достигнет требуемого предела разрешения.

Разобьем видимую часть картинной плоскости на четыре равные части и рассмотрим, каким образом могут соотноситься между собой проекции граней получившейся части картинной плоскости.

Возможны четыре различных случая:

1. Проекция грани полностью накрывает область

2. Проекция грани пересекает область, но не содержится в ней полностью

3. Проекция грани целиком содержится внутри области

4. Проекция грани не имеет общих внутренних точек с рассматриваемой областью

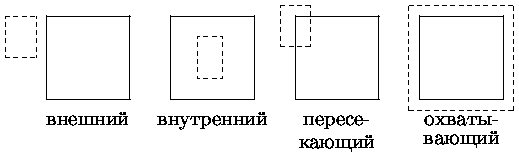
Очевидно, что в последнем случае грань вообще никак не влияет на то, что видно в данной области.

Сравнивая область с проекциями всех граней, можно выделить случаи, когда изображение,

получающееся в рассматриваемой области, определяется сразу:

- Проекция ни одной грани не попадает в область.

- Проекция только одной грани содержится в области или пересекает область. В этом случае

проекции грани разбивают всю область на две части, одна из которых соответствует этой проекции.

- Существует грань, проекция которой полностью накрывает данную область, и эта грань

расположена к картинной плоскости ближе, чем все остальные грани, проекции которых пересекают

данную область. В данном случае область соответствует этой грани.

Если ни один из рассмотренных трех случаев не имеет места, то снова разбиваем область на четыре

равные части и проверяем выполнение этих условий для каждой из частей. Те части, для которых

таким образом не удалось установить видимость, разбиваем снова и т. д.

Алгоритм Вейлера-Азертона

Вейлер и Азертон попытались оптимизировать алгоритм Варнока в отношении числа выполняемых разбиений, перейдя от прямоугольных разбиений к разбиениям вдоль границ многоугольников (1977). Для этого они использовали ими же разработанный алгоритм отсечения многоугольников. Алгоритм работает в объектном пространстве, и результатом его работы являются многоугольники. В самом общем виде он состоит из четырех шагов.

1. Предварительная сортировка по глубине.

2. Отсечение по границе ближайшего к точке наблюдения многоугольника, называемое сортировкой многоугольников на плоскости.

3. Удаление многоугольников, экранируемых более близкими к точке наблюдения многоугольниками.

4. Если требуется, то рекурсивное разбиение и новая сортировка.

В процессе предварительной сортировки создается список приблизительных приоритетов, причем близость многоугольника к точке наблюдения определяется расстоянием до ближайшей к ней вершины. Затем выполняется отсечение по самому первому из многоугольников. Отсечению подвергаются все многоугольники из списка, причем эта операция выполняется над проекциями многоугольников на картинную плоскость. При этом создаются списки внешних и внутренних фигур. Все попавшие в список внешних не экранируются отсекающим многоугольником. Затем рассматривается список внутренних многоугольников и выполняется сортировка по расстоянию до отсекающего многоугольника. Если все вершины некоторого многоугольника оказываются дальше от наблюдателя, чем самая удаленная из вершин экранирующего, то они невидимы, и тогда они удаляются. После этого работа алгоритма продолжается с внешним списком.

Если какая-то из вершин внутреннего многоугольника оказывается ближе к наблюдателю, чем ближайшая из вершин экранирующего многоугольника, то такой многоугольник является частично видимым. В этом случае предварительный список приоритетов некорректен, и тогда в качестве нового отсекающего многоугольника выбирается именно этот "нарушитель порядка". При этом используется именно исходный многоугольник, а не тот, что получился в результате первого отсечения. Такой подход позволяет минимизировать число разбиений.

Этот алгоритм в дальнейшем был обобщен Кэтмулом (1974) для изображения гладких бикубических поверхностей. Его подход заключался в том, что разбиению подвергалась поверхность. Коротко этот алгоритм можно описать так:

1. Рекурсивно разбивается поверхность до тех пор, пока проекция элемента на плоскость изображения не будет покрывать не больше одного пикселя.

2. Определить атрибуты поверхности в этом пикселе и изобразить его.

Эффективность такого метода, как и алгоритм Варнока, зависит от эффективности разбиений. В дальнейшем этот алгоритм был распространен на сплайновые поверхности.

23. >Алгоритм, использующий Z-буфер. (ИЛЮША)

z-буфер – это отдельный буфер глубины, используемый для запоминания координаты z или глубины каждого видимого пиксела в пространстве изображения. В процессе работы глубина или значение z каждого нового пиксела, который нужно занести в буфер кадра, сравнивается с глубиной того пиксела, который уже занесен в z-буфер. Если это сравнение показывает, что новый пиксел расположен впереди пиксела, находящегося в буфере кадра, то новый пиксел заносится в этот буфер и, кроме того, производится корректировка z-буфера новым значением z. Если же сравнение дает противоположный результат, то никаких действий не производится. По сути, алгоритм является поиском по х и у наибольшего значения функции z (х, у).

1. Заполнить буфер кадра фоновым значением интенсивности или цвета.

2. Заполнить z-буфер минимальным значением z.

3. Преобразовать каждый многоугольник в растровую форму в произвольном порядке.

4. Для каждого Пиксел(x,y) в многоугольнике вычислить его глубину z(x,y).

5. Сравнить глубину z(х,у) со значением Zбуфер(х,у), хранящимся в z-буфере в этой же позиции.

Если z(х,у) > Zбуфер (х,у), то записать атрибут этого многоугольника (интенсивность, цвет и т. п.) в буфер кадра и заменить Zбуфер(х,у) на z(х,у). В противном случае никаких действий не производить.

24. >Алгоритм определения видимых поверхностей путем трассировки лучей. (ИЛЮША)

Главная идея, лежащая в основе этого метода, заключается в том, что наблюдатель видит любой объект посредством испускаемого неким источником света, который падает на этот объект и затем каким-то путем доходит до наблюдателя. Свет может достичь наблюдателя, отразившись от поверхности, преломившись или пройдя через нее. Если проследить за лучами света, выпушенными источником, то можно убедиться, что весьма не многие дойдут до наблюдателя. Следовательно, этот процесс был бы вычислительно неэффективен. Аппель первым предложил отслеживать (трассировать) лучи в обратном направлении, т.е. от наблюдателя к объекту, как показано на рисунке. В этом алгоритме предполагается, что сцена уже преобразована в пространство изображения. Перспективное преобразование не используется. Считается, что точка зрения или наблюдатель находится в бесконечности на положительной полуоси z. Поэтому все световые лучи параллельны оси z. Каждый луч, исходящий от наблюдателя, походит через центр пиксела на растре до сцены. Траектория каждого луча отслеживается, чтобы определить, какие именно объекты сцены, если таковые существуют, пересекаются с данным лучом. Необходимо проверить пересечение каждого объекта сцены с каждым лучом. Если луч пересекает объект, то определяются все возможные точки пересечения луча и объекта. Можно получить большое количество пересечений, если рассматривать много объектов. Эти пересечения упорядочиваются по глубине. Пересечение с максимальным значением z представляет видимую поверхность для данного пиксела. Атрибуты этого объекта используются для определения характеристик пиксела.

25. >Построение реалистических изображений. Простая модель освещения для одного источника. (ИЛЮША)

1. Построение реалистичных изображений. Простая модель освещения для одного источника. Определение нормали к поверхности и векторы отражения.

Реал. из-я.: цвет, свет, текстура, преломл. света, перспектива.

Закон Ламберта - падающий свет рассеивается во все стороны с одинаковой интенсивностью. Освещенность точки пропорциональна доле ее площади, видимой от источника.

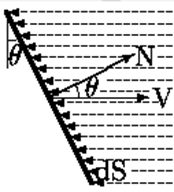
Ir = Ip*Pd*cos(q),

Ir - интенсивность отраженного света,

Ip - интенсивность точечного источника,

0 ≤ Pd ≤ 1 - коэффициент диффузного отражения, зависящий от материала поверхности и длины волны,

0 ≤ q ≤ p/2 - угол между направлением света и нормалью к поверхности.

Учет рассеянного света

I = Ir ·Pr + Ip ·Pd ·cos(q),

Ir - интенсивность рассеянного света,

0 ≤ Pr ≤ 1 - коэффициент отражения рассеянного света.

Учет расстояния

I = Ir·Pr + Ip·Pd·cos(q)/(d + K)

d - расстояние от центра проекции до объекта, при параллельной проекции d - расстояние от объекта, ближайшего к наблюдателю,

K- произвольная константа.

Зеркальное отражение

[L\vec] - ед. вектор направления на источник света.

[N\vec] - нормаль к поверхности.

[R\vec] - ед. вектор направления идеального отражения.

[V\vec] - ед. вектор направления к наблюдателю.

Эмпирическая модель Фонга: Is = Ip W(l, q) cosⁿ(f),

W(l, q) - кривая отражения,

-p/2 ≤ f ≤ p/2,

1 ≤ n ≤ 200

Часто W(l, q) заменяется константой Ks, такой чтобы полученная картина была субъективно приемлема.

Суммарная модель освещения:

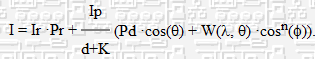
Или при замене W(l, q) на константу Ks:

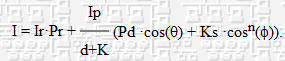
Или:

Если источник света находится на бесконечности, то для данного плоского многоугольника [L\vec] ·[N\vec] равно константе, а [R\vec] ·[V\vec] меняется в пределах многоугольника.

26. >Закраска методом Гуро и методом Фонга. (ИЛЮША)

Метод Гуро

Для того чтобы изобразить объект методом построчного сканирования, нужно в соответствии с моделью освещения рассчитать интенсивность каждого пиксела вдоль сканирующей строки. Нормали к поверхности аппроксимируются в вершинах многоугольников. Однако сканирующая строка не обязательно проходит через вершины многоугольника. При закраске Гуро сначала определяется интенсивность вершин многоугольника, а затем с помощью билинейной интерполяции вычисляется интенсивность каждого пиксела на сканирующей строке.

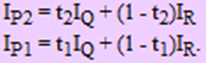
Метод Фонга

используется интерполяция вектора нормали к поверхности вдоль видимого интервала на сканирующей строке внутри многоугольника, а не интерполяция интенсивности. Интерполяция выполняется между начальной и конечной нормалями, которые сами тоже являются результатами интерполяции вдоль ребер многоугольника между нормалями в вершинах. Нормали в вершинах, в свою очередь, вычисляются так же, как в методе закраски, построенном на основе интерполяции интенсивности.

В каждом пикселе вдоль сканирующей строки новое значение интенсивности вычисляется с помощью любой модели закраски. Заметные улучшения по сравнению с интерполяцией интенсивности наблюдаются в случае использования модели с учетом зеркального отражения, так как при этом более точно воспроизводятся световые блики. Однако даже если зеркальное отражение не используется, интерполяция векторов нормали приводит к более качественным результатам, чем интерполяция интенсивности, поскольку аппроксимация нормали в этом случае осуществляется в каждой точке. При этом значительно возрастают вычислительные затраты.

Чтобы закрасить куски бикубической поверхности, для каждого пиксела, исходя из уравнений поверхности, вычисляется нормаль к поверхности. Этот процесс тоже достаточно дорогой. Затем с помощью любой модели закраски определяется значение интенсивности. Однако прежде чем применить метод закраски к плоским или бикубическим поверхностям, необходимо иметь информацию о том, какие источники света (если они имеются) в действительности освещают точку. Поэтому мы должны рассматривать также и тени.

27. >Глобальная модель освещения с трассировкой лучей, формула вычисления значения наблюдаемой интенсивности. Алгоритм трассировки лучей (Шариков)

Модель освещения предназначена для того, чтобы расчитать интенсивность отраженного к наблюдателю света в каждой точке (пикселе) изображения. Она может быть:

· Локальной – принимается только свет, падающий от источников и ориентация поверхности.

· Глобальной – учитывается также свет, отраженный или пропущенный сквозь другие объекты сцены.

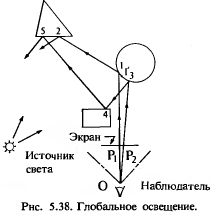
Сфера, параллелепипед и призма зеркальны и непрозрачны.

Наблюдатель смотрит из т. 0 на т.1 на сфере и видит также т.2 на призме, видимую из-за отражения в сфере. Точка 5 отражается от обратной стороны параллелепипеда в т.4 к т.3 на сфере, а затем к наблюдателю.

Отсюда следует, что операции удаления невидимых поверхностей не годятся.

Поэтому из всех алгоритмов удаления невидимых граней остается только метод трассировки лучей.

Т.о., глобальная модель освещения является частью алгоритмов выделения видимых поверхностей путем трассировки лучей.

Глобальная модель освещения Уиттеда.

Уиттед пользуется моделью с такими же членами рассеянного и ламбертовского отражения, а также зеркального отражения Фонга как и в локальной модели освещения

- Интенсивность локальной модели освещения

- единичные векторы нормали к поверхности и направления к источнику,

- единичные векторы, определяющие направления отраженного луча и наблюдения.

Члены, соответствующие глобальному зеркальному отражению и пропусканию рассчитываются по правилу на рис.5.39.

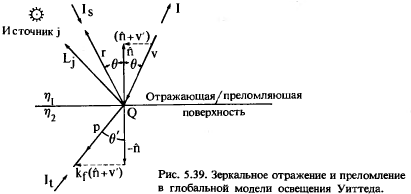
Здесь трассируется луч v, падающий на поверхность в точке Q. В этой точке он отражаетсяв направлении r и, если поверхность прозрачна, преломляется в направлении p. Здесь I_t – интенсивность света, падающего в точку Q по направлению p. Этот свет преломляется и достигает наблюдателя, находящегося в направлении v.

Аналогично, I_s – интенсивность зеркально отраженного света, падающего в направлении r и отраженного к наблюдателю в точке Q.

Lj – направление на j-й источник света, η – показатель преломления среды, n – степень пространственного распределения Фонга для зеркального отражения.

Т.о., наблюдаемая интенсивность I выражается формулой

- интенсивность глобальной модели освещения

- коэффициенты рассеянного, диффузного и зеркального отражения, а k_t – коэффициент пропускания. Суммы по j – диффузное и зеркальное отражение от множества источников.

В отличие от алгоритма построения видимых непрозрачных поверхностей, в котором луч трассируется до первого пересечения с объектом, в глобальной модели работа на этом не кончается.

Здесь предполагается, что падающий луч v в точке Q отражается в направлении r и пропускается сквозь поверхность в направлении p, как показано на рис 5.39. Это значит, что в точке Q образуется ещё 2 луча, для которых нужно найти все пересечения с объектами сцены. Процесс повторяется пока не останется ни одного пересечения.

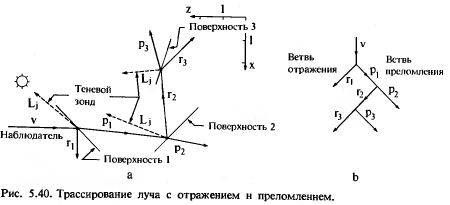
На рис.5.40а он изображен для пересечения луча с одной поверхностью, на рис. 5.40b – соответствующее дерево. Каждый узел дерева представляет собой пересечения луча с поверхностью. Ветвь кончается, когда луч покидает сцену.

При пересечении луча с поверхностью направления отраженного и пропущенного лучей рассчитываются по законам геометрической оптики. Лу r и падающий луч v лежат в одной плоскости, и угол падения = углу отражения. Пропущенный луч преломляется по закону Снеллиуса. В нашей модели направления r и p таковы:

Здесь - отношение показателей преломления, а - вектор единичной нормали в направлении падающего луча. Если знаменатель комплексный, то происходит полное отражение, и предполагается равным нулю.

Для определения интенсивности в каждом пересечении надо пройти дерево в обратном направлении. Интенсивность в узлах рассчитывается в соответствии с моделью освещения, причем для каждого следующего узла она ослабляется с расстоянием между точками пересечения. После прохода всего дерева получается окончательная интенсивность пиксела.

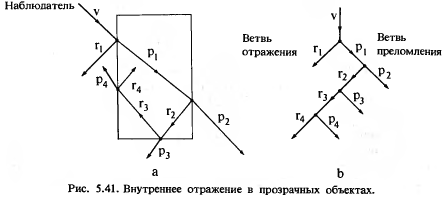
На рис.5.41 показано внутреннее отражение в замкнутом прозрачном теле. Лучи, зеркально отраженные от внутренних граней, остаются внутри объекта и в конце концов поглощаются. Для наблюдателя они невидимы, однако в каждом пересечении луча с поверхностью образуется преломленный луч, который покидает объект и может достичь точки наблюдения. Такие точки должны быть оттрассированы

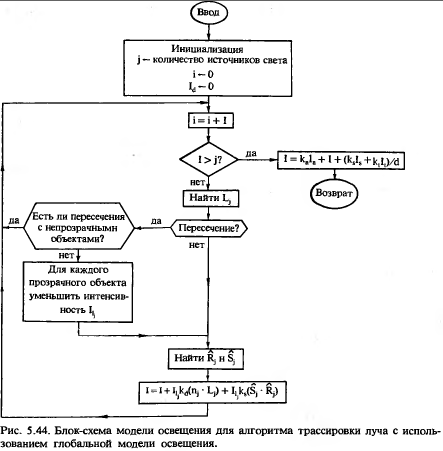
Если изображение цветное, то блок выполняется 3 раза, т.к. RGB.

28. >Цвет в машинной графике. Основные характеристики света и человеческого восприятия цвета. Аддитивная и субтрактивная системы смешения цветов, законы Грассамана. трехмерное цветовое пространство.(Шубарев)

Цвет в машинной графике. Основные характеристики света и человеческого восприятия цвета.

Зрительная система чеповека воспринимает электромагнитную энергию с длинам волн от 400 до 700 нм как видимый свет A нм = 10~9 м). Свет принимается либо непосредственно от источника, например электрической лампочки, либо косвенно при отражении от поверхности объекта или преломлеиии в нем. Источник или объект является ахроматическим, если наблюдаемый свет содержит все видимые длины волн в приблизительно равных количествах. Ахроматический источник кажется белым, а отраженный или преломленный ахроматический свет — белым, черным или серым. Белыми выглядят объекты, ахроматически отражающие более 80% света белого источника, а черными — менее 3%. Промежуточные значения дают различные оттенки серого. Интенсивность отраженного света удобно рассматривать в диапазоне от 0 до 1, где 0 соответствует черному, 1 — белому, а промежуточные значения — серому цвету.

Светлота считается свойством несветящихся или отражающих объектов и изменяется от черного до белого, а яркость является свойством самосветящихся или излучающих объектов и изменяется в диапазоне от низкой до высокой.

Светлота или яркость объекта зависит от относительной чувствительности глаза к разным длипам волн.

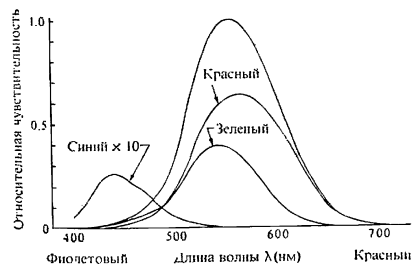
Рис. 5.49. Относительная чувствительность глаза.

Из рис. 5.59 видно, что при дневном свете чувствительность глаза максимальна при длине волны порядка 550 им, а на краях видимого диапазона спектра она резко падает. Кривая на рис. 5.49 называется функцией спектральной чувствительности глаза. Это мера световой энергии или интенсивности с учетом свойств глаза.

Если воспринимаемый свет содержит длины волн в произвольных неравных количествах, то он называется хроматическим.

Психофизиологическое представление света определяется цветовым тоном, насыщенностью и светлотой. Цветовой тон позволяет различать цвета, а насыщенность — определять степень ослабления (разбавления) данного цвета белым цветом. У чистого цвета она равна 100% и уменьшается по мере добавления белого. Насыщенность ахроматического цвета составляет 0%, а его светлота равна интенсивности этого света.

Психофизическими эквивалентами цветового тона, насыщенности и светлоты являются доминирующая длина волны, чистота и яркость. Электромагнитная энергия одной длины волны в видимом спектре дает монохроматический цвет.

Аддитивная и субтрактивная системы смешения цветов

В машинной графике применяются две системы смешения основных цветов: аддитивная — красный, зеленый, синий (RGB) и субтрактивная — голубой, пурпурный, желтый (CMY). Они изображены на рис. 5.51 и цветной вклейке.

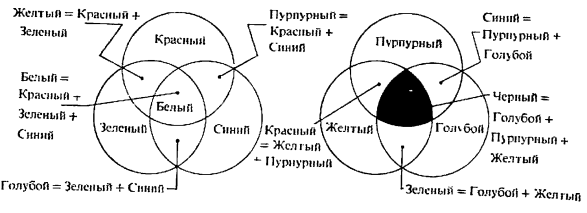
Рис. 5.51. Аддитивная (а) и субтрактивная (б) системы смешения цветов.

Цвета одной системы являются дополнительными к другой: голубой — к красному, пурпурный — к зеленому, желтый — к синему. Дополнительный цвет —

это разность белого и данного цвета: голубой это белый минус

красный, пурпурный — белый минус зеленый, желтый — белый

минут синий. Хотя красный можно считать дополнительным к голубому, по традиции красный, зеленый и синий считаются основными цветами, а голубой, пурпурный, желтый — их дополнениями. Интересно, что в спектре радуги или призмы пурпурного цвета

нет, т. е. он порождается зрительной системой человека.

В субтрактивных системах из спектра белого цвета вычитаются длины волны дополнительного цвета. Например, при отражении или пропускании света сквозь пурпурный объект поглощается зеленая часть спектра.

Законы Грассмана

Координаты цветности МКО для смеси двух цветов определяются по законам Грассмана сложением основных цветов. Смесь цветов С1(х1,у1,z1) и С2(х2,у2,z2) является

Преобразование между двумя аддитивными цветовыми системами по законам Грассмана. Переход от цветового пространства RGB к пространству МКО XYZ:

Цветовые пространства RGB и CMY трехмерны и условно изображаются в виде куба (рис. 5.60).

Началом координат в цветовом кубе RGB служит черный цвет, а в CMY — белый. Ахроматические, т. е. серые цвета в обеих моделях расположены по диагонали от черного до белого, а дополни

тельные цвета лежат в противоположных вершинах.

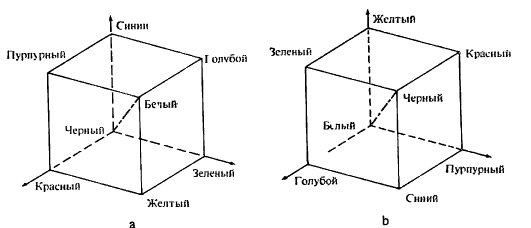
Рис. 5.60. Цветовые кубы: (a) RGB, (b) CMY.

Преобразование между пространствами RGB и CMY выражается следующим образом:

[R G В] = [1 1 1] [С М Y]

29. >Цветовой график МКО, цветовое пространство XYZ, стандартные источники МКО, цветовые охваты, вычисление координат цветности МКО для смеси двух цветов.(Шубарев)

Основные цвета МКО получены из стандартных функций реакции глаза (рис. 5.55). Гипотетические основные цвета МКО обозначаются Х, У, Z.

На самом деле они не существуют, так как без отрицательной части они не могут соответствовать реальному физическому свету. Треугольник XYZ был выбран так, чтобы в него входил весь видимый спектр. Координаты цветности МКО таковы:

и х + у + z — 1. При проекции треугольника XYZ на плоскость

ху получается цветовой график МКО. Координаты цветности х и у

представляют собой относительные количества трех основных цве

тов XYZ, требуемые для составления любого цвета. Однако они не

задают яркость (интенсивность) результирующего цвета. Яркость

определяется координатой У, а X и Z подбираются в соответству

ющем масштабе. При таком соглашении (х, у, Y) определяют как

цветность, так и яркость. Обратное преобразование координат

цветности в координаты цвета XYZ имеет вид

Комиссия МКО решила ориентировать треугольник XYZ таким образом, чтобы равные количества гипотетических основных цветов XYZ в сумме давали белый.

Цветовой график МКО 1931 г. показан на рис. 5.56.

Контур, напоминающий крыло, это геометрическое место точек всех видимых длин волн, т. е. линия спектральных цветностей. Числа на контуре соответствуют длине волны в данной точке. Красный находится в нижнем правом углу, зеленый — вверху, а синий — в левом нижнем углу графика. Отрезок, соединяющий концы кривой, называется линией пурпурных цветностей. Кривая внутри контура соответствует цвету абсолютно черного тела при нагревании от 1000° К до бесконечности. Пунктиром обозначена температура, а также направления, вдоль которых глаз хуже всего различает изменение цвета. Опорный белый — это точка равных энергий Е (х = 0.333, У = 0.333), а стандартные источники МКО — А (0.448, 0.408), В(0.349, 0.352), С(0.310, 0.316), D_65ОО(О.313, 0.329). Источник А аппроксимирует теплый цвет газонаполненной лампы накаливания с вольфрамовой нитью при 2856° К. Он намного «краснее» остальных. Источник В соответствует солнечному свету в полдень, а С — полуденному освещению при сплошной облачности. Источник С принят в качестве опорного белого цвета Национальным комитетом по телевизионным стандартам (NTSC). Источник D_65ОО соответствующий излучению абсолютно черного тела при 6504° К, несколько «зеленее». Он применяется в качестве опорного белого цвета во многих телемониторах.

Как видно из рис. 5.57, цветовой график очень удобен. Чтобы получить дополнительный цвет, нужно продолжить прямую, проходящую через данный цвет и опорный белый, до пересечения с другой стороной кривой. Например, дополнительным к краснооранжевому цвету С4(λ = 610 нм) является синезеленый цвет С5(λ = 491 нм). При сложении в определенной пропорции цвета и его дополнения получается белый. Для того чтобы найти доминирующую длину волны цвета, нужно продолжить прямую, проходящую через опорный белый и данный цвет, до пересечения с линией спектральных цветностей. Например, на рис. 5.57 доминирующая длина волны цвета С6 равна 570 нм, т. е. она желтозеленая. Если прямая пересекает линию пурпурных цветностей, то у этого цвета нет доминирующей длины волны в видимой части спектра. В этом случае она определяется как дополнительная доминирующая длина волны с индексом «с», т. е. прямая продолжается от цвета через опорный белый в обратном направлении. Например, доминирующая длина волны цвета С7 на рис. 5.57 равна 500 нм. Чистые или полностью (на 100%) насыщенные цвета лежат на линии спектральных цветностей. Опорный белый считается «полностью разбавленным», т. е. его чистота равна 0%. Чтобы вычислить чистоту промежуточных цветов, надо найти отношение расстояния от опорного белого до данного цвета к расстоянию от опорного белого до линии спектральных или пурпурных цветностей. Например, чистота цвета С6 на рис. 5.57 равна а /(a +b), а С7 равна с /(с + d).

Координаты цветности МКО для смеси двух цветов определяются по законам Грассмана сложением основных цветов. Смесь цветов С1(х1,у1,z1) и С2(х2,у2,z2) является

ВОПРОСЫ НА КОНС

1) при разбиении невыпуклых многоугольников на выпуклые как будут выглядеть 2 многоугольника в первой итерации

2) зачем нужны пробные функции отсекателя в трехмерном алгоритме разбиения средней точкой