7. Развертка окружности. Преобразование отрезков. Развертка эллипса.

Развёртка окружности:

Уравнение окружности: x²+y²=R²

Достаточно построить 1/8 часть, остальные могут быть получены отражениями.

Генерировать будем из точки х=0, у=R по часовой стрелке.

На каждом шаге алгоритм выбирает точку P_j(x_j,y_j) ближайшую к окружности одним из трех способов:

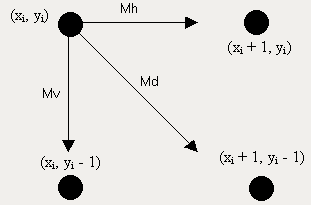
Возможные типы пересечения окружности и растровой сетки:

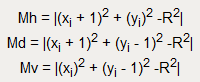
Выбирается минимальное значение

Разность между квадратами расстояний от центра окружности до диагонального пиксела (хi + 1, yi - 1) и от центра до точки на окружности R² равна Δi = (xi + 1)² + (yi - 1)² - R².

Как и в алгоритме Брезенхема для отрезка, для выбора соответствующего пиксела желательно использовать только знак ошибки, а не ее величину.

При Δi < 0 диагональная точка (хi + 1, yi - 1) находится внутри реальной окружности, т. е. это случаи 1 или 2 на рис. 2.8. Ясно, что в этой ситуации следует выбрать либо пиксель (хi + 1, yi), т. е. Mh, либо пиксель (хi + 1, yi - 1), т. е. Md. Для этого сначала рассмотрим случай 1 и проверим разность квадратов расстояний от окружности до пикселов в горизонтальном и диагональном направлениях:

δ = |(xi + 1)² + (yi)² - R²| - |(xi + 1)² + (yi - 1)² - R²|

При δ < 0 расстояние от окружности до диагонального пиксела (Md) больше, чем до горизонтального (Mh). Напротив, если δ > 0, расстояние до горизонтального пиксела (Mh) больше. Таким образом,

при δ <= 0 выбираем Mh в (xi + 1, yi)

при δ > 0 выбираем Md в (xi + 1, yi - 1)

При δ = 0, когда расстояние от окружности до обоих пикселов одинаковы, выбираем горизонтальный шаг.

Количество вычислений, необходимых для оценки величины δ, можно сократить, если заметить, что в случае 1

(xi + 1)² + (yi)² - R² >= 0

(xi + 1)² + (yi - 1)² -R² < 0

так как диагональный пиксел (xi + 1, yi - 1) всегда лежит внутри окружности, а горизонтальный (xi + 1, yi) - вне ее. Таким образом, δ можно вычислить по формуле

δ = (xi + 1)² + (yi)² - R² + (xi + 1)² + (yi - 1)² - R²

Дополнение до полного квадрата члена (yi)2 с помощью добавления и вычитания -2yi + 1 дает

δ = 2[(xi + 1)² + (yi - 1)² - R²] + 2yi -1

В квадратных скобках стоит по определению Δi, и его подстановка

δ = 2(Δi + yi) - 1

Преобразование отрезков

алгоритм Брезенхема

этот алгоритм выбирает оптимальные растровые координаты для представления отрезков. Одна из координат (x или y), в зависимости от углового коэффициента, изменяется на 1. изменение другой координаты зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. это расстояние называется ошибкой. алгоритм построен на проверке знака этой ошибки.

решение принимается в зависимости от того, проходит ли прямая выше середины точки (1/2). в этом и заключается оптимальность алгоритма.

Алгоритм построен так, что требуется проверять лишь знак этой ошибки.

Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0, 0) больше чем 1/2, то его пересечение с прямой x = 1 будет расположено ближе к прямой y = 1, чем к прямой y = 0. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента, равного 1/2, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1).

Не все отрезки проходят через точки растра.

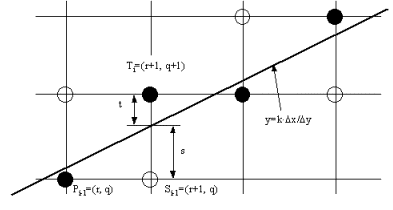
Изображаемый отрезок проводится из точки (x1, y1) в точку (x2, y2). Пусть первая точка находится ближе к началу координат, тогда перенесем обе точки, T(x1, y1) так, чтобы начальная точка отрезка оказалась в начале координат, тогда конечная окажется в (D x, D y), где D x= x2- x1 , D y= x2- x1. Уравнение прямой теперь имеет вид y=x× D y/Dx. Из рисунка следует, что

поэтому

помножим на D x:

так как D x>0, величину D x(s-t) можно использовать в качестве критерия для выбора пиксела. Обозначим эту величину di :

так как r = xi-1, q = yi-1, получаем:

Известно, что xi - xi-1=1. Если di >= 0, то выбираем Ti, тогда

Если di <0, то выбираем Si, тогда

Таким образом, мы получили итеративную формулу для вычисления критерия di.

Развёртка эллипса:

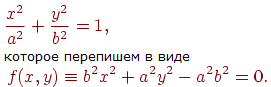
В каждой точке (x,y) эллипса существует вектор нормали, задаваемый градиентом функции f. Дугу разобьем на две части: первая - с углом между нормалью и горизонтальной осью больше 45° (тангенс больше 1) и вторая - с углом, меньшим 45°. Движение вдоль дуги будем осуществлять в направлении по часовой стрелке, начиная с точки (0,b). Вдоль всей дуги координата является монотонно убывающей функцией от x, но в первой части она убывает медленнее, чем растет аргумент, а во второй - быстрее. Поэтому при построении растрового образа в первой части будем увеличивать x на единицу и искать соответствующее значение y, а во второй - сначала уменьшать значение y на единицу и определять соответствующее значение x.

Направление нормали соответствует вектору

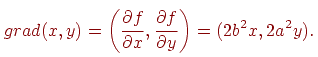
Отсюда находим тангенс угла наклона вектора нормали: . Приравнивая его единице, получаем, что координаты точки деления дуги на вышеуказанные части удовлетворяют равенству . Поэтому критерием того, что мы переходим ко второй области в целочисленных координатах, будет соотношение , или, переходя к целочисленным операциям, .

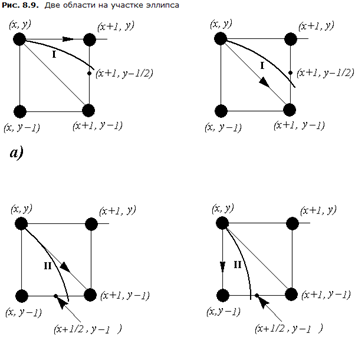
При перемещении вдоль первого участка дуги мы из каждой точки переходим либо по горизонтали, либо по диагонали, и критерий такого перехода напоминает тот, который использовался при построении растрового образа окружности. Находясь в точке (x,y), мы будем вычислять значение . Если это значение меньше нуля, то дополнительная точка лежит внутри эллипса, следовательно, ближайшая точка растра есть , в противном случае это точка .

На втором участке дуги возможен переход либо по диагонали, либо по вертикали, поэтому здесь сначала значение координаты y уменьшается на единицу, затем вычисляется и направление перехода выбирается аналогично предыдущему случаю.

Остается оптимизировать вычисление параметра , умножив его на 4 и представив в виде функции координат точки. Тогда для первой половины дуги имеем

Для второй половины дуги получим

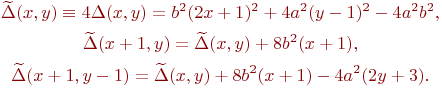
8. >Развертка многоугольников (Домрачев).

Алгоритмы развертки многоугольников заключаются в том, что построчно определяется, лежит ли точка внутри контура или нет. В затравочных алгоритмах используется точка внутри области и от нее идет закраска в стороны.

Для разработки эффективного метода учитывается то, что соседние пикселы, кроме граничных, обладают одинаковыми свойствами. Поэтому контур сканируется снизу вверх построчно и выделяются точки пересечения ребер. Внутренняя часть закрашивается. Т.к. координаты пиксела определяются его нижним левым углом, то, во избежание ошибок, сканирующая строка ищет пересечения с серединами пикселов.

Проблема возникает при пересечении сканирующей строкой вершины. В этом случае необходимо проверить, является ли вершина экстремальной, для этого проверяются координаты смежных ребер и если обе координаты лежат выше или ниже координат вершины, то вершина экстремальна. Если точка экстремальна, то учитывать ее надо дважды, иначе - один раз.

Горизонтальные ребра игнорируются.

Алгоритмы на основе данных суждений называются алгоритмами с упорядоченным списком ребер. Их эффективность зависит от эффективности используемой сортировки.

9. >Алгоритм заполнения гранично-заданных областей. (Домрачев)

В алгоритмах с затравкой известен хотя бы один пиксел из области многоугольника. Алгоритм пытается найти и закрасить все другие пикселы внутри контура. Обычно используется алгоритм со стеком: Взять пиксел из стека. Закрасить. Для соседних 4 пикселов проверить, не является ли он граничным, или не присвоено ли ему уже требуемое значение. Проигнорировать его в любом из этих двух случаев. Иначе поместить в стек.

Есть так же построчный алгоритм: Затравочный пискел извлекается из стека. Интервал заполняется влево и вправо по строке, пока не будет найдена граница. Запоминаются крайний левый и крайний правый пикселы интервала. В этом диапазоне проверяются строки сверху и снизу. Если на них есть незаполненные пикселы, то крайний правый в каждом таком интервале помещается в стек.

Этот алгоритм справляется с дырами.

10. >Геометрические преобразования. Однородные координаты, композиция преобразований (масштабирование, поворот, перенос на плоскости и в пространстве). (Домрачев)

Однородные координаты ― координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же ненулевое число.