15. Работа с матрицами

Табличный процессор Excel позволяет производить обработку данных, представленных в виде матриц.

Матрицей размерности (mn) называется прямоугольная таблица из mn чисел a_ij (элементов матрицы):

,

где m – число строк матрицы, n – число столбцов, а_ij – элемент стоящий в i-й строке и j-м столбце ( ) .

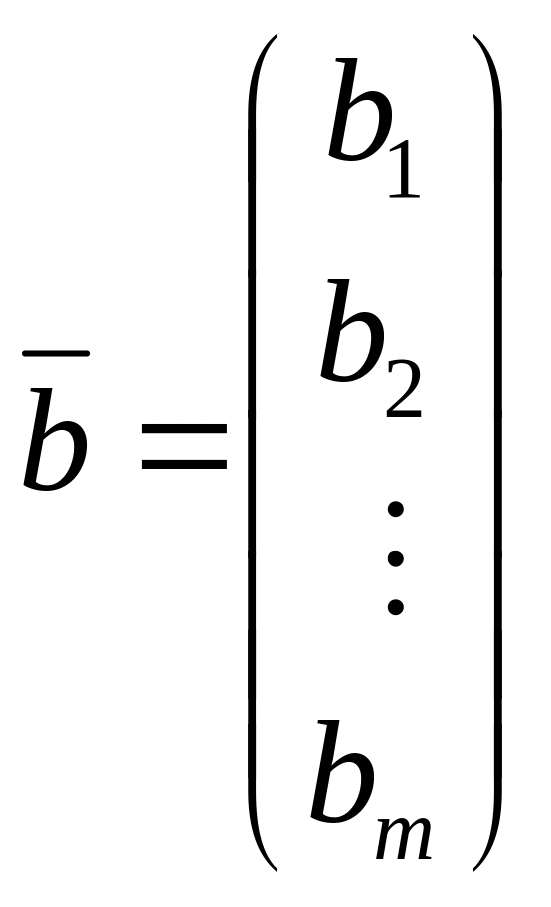
Столбец — это матрица размерности (m1).

Строка — это матрица размерности (1n).

Матрица размерности (nn) называется квадратной порядка n.

Понятие матрицы связано с понятием массива. В теории информатики под массивом понимают область памяти ячеек, имеющих одинаковое имя, но разные индексы. Индексы указывают на номер строки и столбца ячейки в области памяти. Они определяют тип и размерность массива и записываются внутри круглых скобок. Так, например, массив А(1), А(2), …, А(14) является одномерным. Ниже представлен двумерный массив с девятью ячейками:

А(1,1), А(1,2), А(1,3)

А(2,1), А(2,2), А(2,3)

А(3,1), А(3,2), А(3,3)

Ячейка А(1,2) находится на пересечении первой строки и второго столбика, А(2,2) — на пересечении второй строки и второго столбика.

Принято следующее обозначение массива: А(i, j), где A — имя массива, i = 1, m; j = 1, n. Количество ячеек массива равно mxn. В ячейки массива вводятся определенные значения. Индексы имен ячеек массива однозначно определяют место введенному значению в некоторой области памяти, что позволяет вывести на экран монитора или на бумагу содержимое всего массива, которое и представляется матрицей.

Процесс выполнения матричных операций в таблицах Excel можно разбить на четыре этапа:

• На первом этапе выделяется область, в которую будут помещаться элементы новой матрицы, полученной в результате выполнения матричной операции. Размер области (число ячеек по вертикали и по горизонтали) должен совпадать с размером матрицы результата.

• Второй этап предназначен для вызова соответствующей матричной функции. Поиск функции лучше выполнять с помощью Мастера функций. Функцию можно также непосредственно указать в верхней левой ячейке выделенной области.

• На третьем шаге необходимо указать область или области, из которых выбираются элементы матриц, участвующих в операции, выделив эту область мышью.

• Четвертый этап позволяет произвести выполнение матричной операции (путем нажатия клавиши F2, а затем комбинации клавиш Ctrl+Shift+Enter).

Рассмотрим подробнее процесс выполнения матричных операций на примерах транспонирования, умножения и обращения матриц.

Транспонирование матрицы

Транспонированной матрицей называется матрица, у которой строки заменены столбцами. Такая матрица обозначается А^Т. Итак, если

А = (a_ij)_mn, то A^T = (a_ji)_nm .

Для транспонирования матриц в таблицах Excel используется функция ТРАНСП. Эта функция меняет ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот, т. е. первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и так далее. Предложенное ниже упражнение демонстрирует применение функции ТРАНСП.

Упражнение 15.1

Цель — транспонирование матрицы.

Выполните следующий порядок действий:

• З аполните диапазон ячеек В2:D4 любыми числами.

– В столбике А перед матрицей введите ее обозначение: А =

– Выделите диапазон ячеек (например, В5:D7), в который будет записываться матрица А^Т.

– Перед матрицей введите ее обозначение: А^Т =

• Затем вызовите Мастер функций, щелкнув по соответствующей кнопке, или выполните команду Вставка /Функции.

• В поле Категория выберите Ссылки и массивы.

• В поле Функция выберите ТРАНСП, затем нажать Ok.

• Появившееся окно ТРАНСП переместите в любое место листа для открытия диапазона ячеек В2:D4. Выделите этот диапазон (рис. 15.1), после чего нажать Ok.

• Нажмите на клавиатуре клавишу F2.

• Затем нажмите комбинацию клавиш Ctrl+Shift+Enter.

Результат выполнения всех команд показан на рисунке 15.2.

Рис. 15.1. Рис. 15.2.

Функция МУМНОЖ возвращает произведение матриц. Результатом является массив с таким же числом строк, как массив 1 и с таким же числом столбцов, как массив 2.

Упражнение 15.2

Цель — умножение матриц С = A • B.

Выполните следующий порядок действий:

– Заполните диапазон ячеек В2:D4 числами.

– То же самое произвести с диапазоном ячеек B6:D8.

– Ввести обозначения матриц с использованием символа и букв А и В.

– Выделить блок ячеек В11:D13, в который будет записываться матрица С.

– Ввести для нее необходимые символы обозначения.

– Вызвать Мастер функций.

– В поле Категория выбрать Математические.

– В поле Функция выбрать МУМНОЖ.

– В поле Массив 1 указать В2:D4, а в поле Массив 2 указать В6:D8.

– Нажать F2, затем Ctrl+Shift+Enter.

Обращение матрицы

Пусть А – квадратная матрица порядка n. Матрица А^–1 называется обратной для матрицы А, если АА^–1 = А^–1А = Е, где Е – единичная матрица порядка n (рис. 15.3). В единичной матрице элементы главной диагонали равны 1, а остальные — нулевые.

Рис. 15.3.

В таблицах Excel для создания обратной матрицы, хранящейся в массиве, применяется функция МОБР. Рассмотрим на ниже предложенном упражнении создание обратной и единичной матриц.

Упражнение 15.3

Цель — создание обратной и единичной матрицы.

Выполните следующий порядок действий:

• Заполнить диапазон ячеек В2:D4 числами.

• Выделить диапазон ячеек B6:D8.

• Затем вызовите Мастер функций, щелкнув по соответствующей кнопке.

• В поле Категория выберите Ссылки и массивы.

• В поле Функция выберите МОБР, затем нажмите Ok.

• Появившееся окно МОБР переместите в любое место листа для открытия диапазона ячеек В2:D4. Выделите этот диапазон (см. рис. 15.1), после чего нажмите Ok.

• Нажмите на клавиатуре клавишу F2, затем — комбинацию клавиш Ctrl+Shift+E.

• Выделить блок ячеек В11:D13, в который будет создаваться единичная матрица Е, как результата умножения исходной матрицы А на ее обратную А^-1.

• Ввести для нее необходимые символы обозначения.

• Вызвать Мастер функций.

• В поле Категория выбрать Математические.

• В поле Функция выбрать МУМНОЖ.

• В поле Массив 1 указать В2:D4, а в поле Массив 2 указать В4:D8.

• Нажать F2, затем Ctrl+Shift+Enter.

• Выполните по необходимости округление элементов полученной матрицы до появления нулей.