
- •Часть 1. Конспекты лекций
- •Правила комбинаторики
- •Основные понятия комбинаторики
- •1.2. Основные понятия теории вероятностей
- •Начальные понятия теории вероятностей
- •Определения вероятности событий
- •Лекция 2. Основные теоремы теории вероятностей случайных событий
- •2.1. Действия над событиями
- •2.2. Вероятность суммы событий
- •Следствия из теоремы сложения
- •2.3. Вероятность произведения событий
- •2.4. Формула полной вероятности. Формула Байеса.
- •2.5. Теорема Бернулли
- •2.6. Предельные теоремы в схеме Бернулли.
- •3. Интегральная теорема Муавра-Лапласа
- •3.1. Начальные понятия
- •3.2. Функция распределения свх f(X) (интегральная функция распределения)
- •3.3. Функция плотности вероятности нсв f(X)
- •3.4. Числовые характеристики случайных величин
- •3.5. Виды законов распределения случайных величин
- •1. Биномиальный закон распределения
- •2. Закон Пуассона
- •3. Нормальное распределение (закон Гаусса)
- •4 .Логнормальное распределение
- •3.6. Вероятность попадания нсв х в заданный промежуток
- •4.1. Система двух дискретных случайных величин (двумерная дискретная св)
- •Начальные понятия.
- •Числовые характеристики системы двух св
- •4.2. Предельные теоремы теории вероятностей
- •Закон больших чисел
- •5.1.Предмет математической статистики. Генеральная и выборочная совокупность.
- •5.2. Статистическое распределение выборки и его графическое изображение
- •5.3. Числовые характеристики статистического распределения
- •6.1. Оценка параметров генеральной совокупности по выборке
- •Свойства статистических оценок
- •Точечные оценки математического ожидания, дисперсии и вероятности.
- •Интервальное оценивание параметров.
- •Доверительные интервалы для параметров нормального распределения
- •Интервальная оценка параметров генеральной лингвистической совокупности.
- •Число степеней свободы
- •Определение минимально достаточного объёма выборки в грамматических, фонетико-фонологических и лексикологических исследованиях.
- •6.2. Проверка статистических гипотез. Исследование вероятностных свойств языка и статистики текста с помощью метода гипотез
- •Проверка лингвистических гипотез с помощью параметрических критериев
- •Проверка гипотез с помощью непараметрических критериев
- •Критерий Пирсона
- •Часть 2. Вопросы и задания для практических работ.
- •1. Элементы комбинаторики
- •Часть 3. Задания для самостоятельной работы
- •1. Графический способ.
- •2. Критерий асимметрии и эксцесса.
- •3. Критерий Колмогорова-Смирнова.
- •4. Критерий Пирсона
- •Приложение 1.1. Значения интегральной функции Лапласа
- •2.Место модуля в структуре ооп:
- •3.Краткое содержание модуля тв и мс.
- •4. Компетенции обучающегося, формируемые в результате освоения модуля тв и мс дисциплины «Основы математической обработки информации»
- •5. Структура и содержание модуля тв и мс дисциплины «Основы математической обработки информации»
Оглавление
Введение |
5 |
Часть 1. Конспекты лекций |
8 |
Лекция 1. Комбинаторика. Начальные понятия теории вероятностей |
8 |
Лекция 2. Основные теоремы теории вероятностей случайных событий |
20 |
Лекция 3. Случайная величина |
30 |
Лекция 4. Система двух дискретных случайных величин. Предельные теоремы теории вероятностей |
41 |
Лекция 5. Основы математической статистики. |
49 |
Лекция 6. Элементы теории статистических оценок и проверки гипотез |
59 |
Часть 2. Вопросы и задания для практических работ |
74 |
Практическая работа 1. Элементы комбинаторики. Основные понятия теории вероятностей |
74 |
Практическая работа 2. Основные теоремы теории вероятностей |
77 |
Практическая работа 3. Случайные величины |
79 |
Практическая работа 4 Элементы математической статистики |
82 |
Часть 3. Задания для самостоятельной работы |
84 |
Часть 4. Лабораторные работы |
89 |
Лабораторная работа 1. Первичная обработка лингвистической информации. |
89 |
Лабораторная работа 2. Проверка гипотезы о нормальности распределения глагольных форм в литературных текстах |
91 |
Лабораторная работа 3 Оценка параметров нормально распределённой лингвистической случайной величины по выборке. |
95 |
Лабораторная работа 4. Проверка гипотезы о статистической значимости различия средних частот употребления глаголов |
97 |
Лабораторная работа 5 Корреляционный анализ. Построение модели линейной регрессии лингвистической информации |
99 |
Лабораторная работа 6. Однофакторный дисперсионный анализ. Исследование влияния стиля речи на частоту употребления глагольных форм |
101 |
Список рекомендованной литературы |
106 |
Список использованной литературы |
106 |
Приложение 1. Таблицы математической статистики |
108 |
1.1. Значения интегральной функции Лапласа |
108 |
1.2.
Критические значения
|
109 |
1.3. Критические значения критерия t (распределение Стьюдента) |
110 |
1.4. Критические значения F-Фишера (для проверки направленных альтернатив) |
111 |
1.5. Критические значения F-Фишера (для проверки ненаправленных альтернатив) |
112 |
Приложение 2 . Программа учебного модуля «Теория вероятностей и математическая статистика» |
113 |
Введение
Наша жизнь состоит из случайностей. Случайные явления происходят повсюду, в том числе и в филологии. Случайна последовательность букв или фонем в слове, слов в предложении, последовательность предложений в тексте или речи, длина слов и предложений, частота употребления различных частей речи. Случайной является высота звуков человеческой речи и восприятие человеком определённых текстов и т.п. Но среди случайного, и, как кажется, непредсказуемого, наблюдаются закономерности. Эти закономерности, которые присущи массовым случайным явлениям и изучает теория вероятностей.
Теория вероятностей – теоретическая наука, но её положения стали основой «Математической статистики» раздела математики, который изучает методы обработки и анализа результатов массовых случайных явлений с целью выявления статистических закономерностей. Математическая статистика имеет дело с практическими данными, полученными как результат наблюдений. Две эти науки обычно рассматривают совместно, так как применение математических моделей одной из них невозможно без использования другой.
Теория вероятностей и математическая статистики (ТВ и МС) широко применяются в гуманитарных науках, в том числе и в филологии. Наибольшее применение методы этого раздела математики находят в лингвистических исследованиях, так как именно для лингвистики характерна бо́льшая близость к точным наукам, чем для других дисциплин, традиционно относимых к филологии.
Первоначально математические методы являлись лишь вспомогательным средством лингвистического анализа, но уже в середине XIX – начале XX века стали составлять основу большинства лингвистических исследований. В настоящее время вероятностно-статистические методы применяются в различных видах лингвистического анализа: стилистическом, диахроническом, типологическом, в социолингвистике, психолингвистике, лексикографии и других.
На необходимость использования методов ТВ и МС в языкознании указывают в своих трудах известные лингвисты В.В. Виноградов, Р.Г. Пиотровский, А.В. Гладкий, В.А. Звегинцев, М.В. Панов, Н.Ф. Алефиренко, Б.Н. Головин и другие.
Например, Б.Н. Головин в труде «Язык и статистика» определяет основания вероятностно-статистического изучения языка и речи.
1) Объективная присущность языку количественных признаков, количественных характеристик: анализ всех грамматических категорий устанавливает их относительный функциональный вес в разных стилях литературного языка, соотношения между словами, слогами и фонемами позволяют дать классификацию языков, которую можно использовать и при изучении их истории.
2) Внутренняя зависимость, существующая между качественными и количественными характеристиками языковой структуры: количественные различия на низшем уровне дают качественные различия на высшем уровне: количество фонем в языке отражается на качестве морфем и слов, количество морфем – на качестве слов, количественные характеристики на морфологическом уровне дают о себе знать в качестве синтаксических явлений.
3) Частоты различных элементов подчиняются статистическим законам: полученные опытным путём данные о частотах и вероятностях частей речи, некоторых типов предложений, формах глагола говорят о колебаниях частоты каждого изучавшегося элемента языка около некоторой средней величины, причём колебания эти статистически закономерны. [Головин, 1971, с.11].
«Язык может рассматриваться как структура, элементы которой и функционируют в речи и развиваются, подчиняясь тем или иным вероятностно-статистическим законам». [Головин, 1971, с.16].
Широкое применение методов теории вероятностей и математической статистики в лингвистике стало возможным лишь с применением вычислительной техники. Появление ЭВМ и их способность перерабатывать огромные объёмы информации позволили значительно расширить поле лингвистического исследования.
Применяя математические методы, необходимо иметь в виду, что филологические законы имеют совсем другую природу, чем законы точных наук. Большинство закономерностей гуманитарной сферы, складываясь под действием случайных факторов, проявляются статистически, т.е. оказываются верными не в каждом отдельном случае, а только в среднем, при многократном повторении с одними и теми же данными.
Часть 1. Конспекты лекций
Лекция 1 1.1. Комбинаторика.
Лингвисту часто приходится решать задачи, в которых требуется из конечного множества лингвистических элементов по заданным правилам составлять различные комбинации и производить подсчёт таких комбинаций. Например, «синтаксисту важно знать, сколько позиционных вариантов может давать в устно-разговорной речи предложение “Сегодня идёт дождь”, фонетисту - сколько, двух- и трёхбуквенных комбинаций может дать русский алфавит» (Пиотровский, 1977, с. 110). Задачи такого вида называются комбинаторными, а раздел математики, в котором решают такие задачи – комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о числе различных подмножеств (комбинаций), подчинённых тем или иным условиям, которые можно составить из элементов конечного множества.
Комбинаторика широко применяется на практике, в том числе и в языкознании. По словам В.М. Солнцева “способность к комбинаторике есть общее и обязательное свойство единиц языка, обусловленное общесистемными фундаментальными свойствами единиц языка – дискретностью и неоднородностью” (Солнцев, 1977, с. 268).
Комбинаторика связана с другими разделами математики, в том числе с теорией вероятностей, имеет широкий спектр применения в различных областях знаний.
Основоположником современной комбинаторики считается Г. Лейбниц, который ввёл термин «комбинаторика» в математический обиход в 1666 году, опубликовав свой труд «Рассуждения о комбинаторном искусстве». Наряду с Готфридом Лейбницем, большой вклад в развитии комбинаторики, как науки, внесли Блез Паскаль и Якоб Бернулли. Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера.
Правила комбинаторики
Многие задачи комбинаторики решаются с помощью двух основных правил: правила сложения и правила умножения.
Правило
сложения.
Пусть
элемент А можно выбрать
 способами, элемент В – другими
способами, элемент В – другими
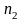 способами. Тогда элемент А
или В
можно выбрать
способами. Тогда элемент А
или В
можно выбрать
 способами.
способами.
Пример. На первой полке 10 книг, а на второй 12. Сколькими способами можно выбрать книгу с одной из этих полок?
Так как книгу с первой полки (элемент А) можно выбрать 10 способами, а книгу со второй (полки элемент В) – 12 способами, то книгу с первой или второй полки (элемент А или В) можно выбрать 10+12=22 способами.
Правило умножения. Пусть элемент А можно выбрать способами, при каждом выборе А элемент В можно выбрать способами,
Тогда
элемент А
и В
можно выбрать
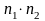 способами.
способами.
Пример. Сколько слов можно получить, если для корня «изб» выбирается один из 3 суффиксов: «ушк», «ёнк», «ушечк», и одно из двух окончаний: «а», «и».
Есть 3
способа выбора суффикса и 2 способа
выбора окончания, поэтому суффикс и
окончание можно выбрать 3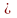 2=6
способами, т.е. получится 6 слов.
2=6
способами, т.е. получится 6 слов.
Правила верны и для большего числа элементов.
Основные понятия комбинаторики
Размещение из n элементов по m (m≤ n) – упорядоченное (важен порядок расположения элементов) подмножество из m элементов множества, которое содержит n различных элементов. Все m элементов размещения различны.
Например, все размещения из 3 элементов множества {A,B,M} по 2 составляют следующее множество:
{{A,B},{A,M},{B,M},{B,A}, {M,A}, {M,B}}.
Два размещения отличаются составом или порядком расположения элементов.
В комбинаторных задачах нас интересуют не сами размещения, а их количество.
Число
размещений
из n
элементов по m
обозначается
 и находится по формуле:
и находится по формуле:
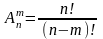 ,
,
где n! (n-факториал) – произведение n первых натуральных чисел:
1! =1; 2!=1 2=2; 3!= 1 2 3=6; 4!= 1 2 3 4=24;
n!= 1 2 3 … n (при n>2) 0!=1
Пример. Имеется алфавит из 20 букв. Сколько можно составить трёхбуквенных «слов», если буквы в «слове» не повторяются?
Так как при составлении слова важен порядок расположения букв, то для решения задачи найдём число размещений из 20 по 3:
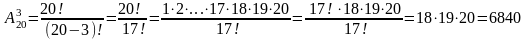
Перестановка из n элементов – это размещение из n различных элементов по n. Чтобы получить разные перестановки выбирают все n элементов множества и меняют их местами.
Например, все перестановки из 3 элементов множества {f; p;q} составляют следующее множество: {{f;p;q}, {f;q;p}, {p;q;f}, { p;f;q}, {q;f;p}, {q;p;f}}.
Две перестановки отличаются только порядком расположения элементов
Число
перестановок из n
элементов обозначается
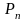 и определяется по формуле:
и определяется по формуле:

Пример. Сколько предложений можно составить из 4 слов: «увы», «сегодня», «идёт», «дождь»?
Так как
для составления предложений берут все
заданные слова и меняют их местами, то
полученные предложения – перестановки
из 4 элементов. Число предложений
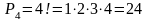
Сочетание из n элементов по m (m≤ n) - неупорядоченное подмножество из m элементов, множества, которое содержит n различных элементов. Все m элементов сочетания различны.
Например, все сочетания из 4 элементов множества{A,B,M} по 2
составляют следующее множество: {{A,B},{A,M},{B,M}}
Два сочетания отличаются только составом элементов.
Число
сочетаний
из n элементов по m обозначается
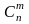 и находится по формуле:
и находится по формуле:
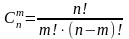
Пример. Из 10 гостей выбирают 2 для участия в конкурсе. Сколько имеется способов выбора?
При
выборе 2 гостей не важен порядок их
выбора, поэтому находим число сочетаний
из 10 по 2:
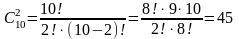
Число перестановок, размещений, сочетаний с повторениями (для тех случаев, когда среди образующих элементов есть одинаковые)
Число
перестановок
из n элементов с
повторениями,
где ni - количество одинаковых элементов
в i – той группе:
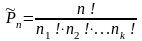 .
.
Пример. Найти количество комбинаций, которые можно составить из букв слова «математика».
Так как в слове «математика» буквы повторяются (м-2 раза, а-3 раза, т-2 раза), то полученные буквосочетания являются перестановками с повторением.
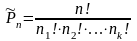 ;
;
Число
размещений
из n элементов по m
с
повторениями:
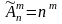
Пример. Сколько можно составить 2-буквенных комбинаций для денежных знаков из 30 букв русского алфавита ( без ъ, й, ь)?
Так как
буквы в серии денежных знаков могут
повторяться, то это размещения с
повторениями: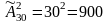
Число
сочетаний
из n элементов по m с
повторениями
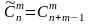
Пример. В некотором языке имеются 2 типа фонем: гласные и согласные, причём слово может быть образовано из одних гласных, из одних согласных, а также из гласных и согласных. Необходимо определить, сколькими способами можно составить 3-фонемное слово [22].
Так как выбираются 3 фонемы из 2 типов, причём типы фонем в слове могут повторяться, то число способов составления 3-фонемного слова
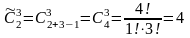
Эти способы можно перечислить: слово состоит из одних гласных, из одних согласных, из двух гласных и одной согласной и из одной гласной и двух согласных.

 (распределение Пирсона)
(распределение Пирсона)