Средние индексы

Когда имеющаяся информация не позволяет рассчитать агрегатный индекс, прибегают к вычислению средневзвешенных индексов.

Опр.7. Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.

Устно: Он должен быть тождественен агрегатному индексу. Для вычисления средних индексов, используют две формулы средних: арифметическая и гармоническая. Вспомним их общий вид:

средняя арифметическая взвешенная;

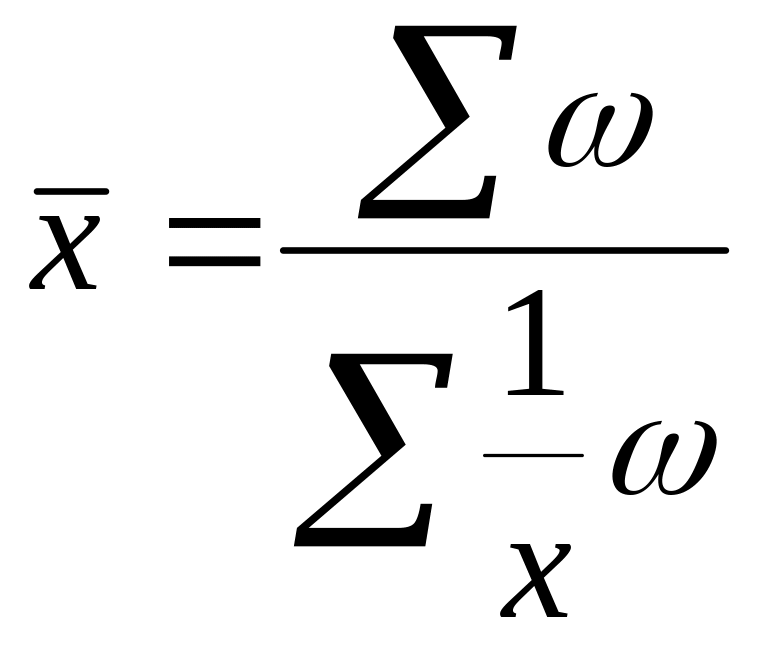средняя гармоническая.

Средний арифметический индекс будет тождественен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.

Например, средний арифметический индекс физического объема имеет вид:

,

так как , то имеем:

.

Замечание: средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. Индексы качественных показателей определяются по формуле средней гармонической взвешенной величины.

Средний гармонический индекс тождественен агрегатному индексу, если индивидуальные индексы будут взвешены с помощью слагаемых числителя агрегатного индекса.

Например, индекс цен можно вычислить так:

,

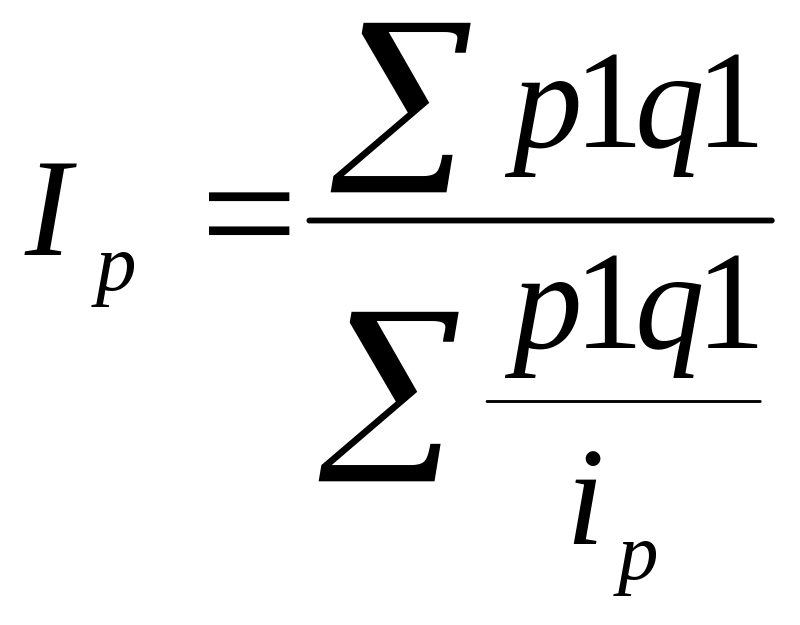так как , то имеем:

.

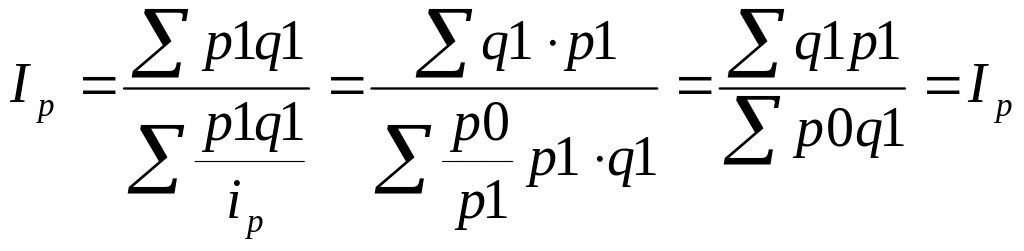Таким образом, весами при определении индекса цен, является стоимость продукции текущего периода.

Замечание1. Средние индексы широко используются для анализа рынка ценных бумаг. Наиболее известными являются индексы Доу-Джонса, Стэндарда и Пура.

Индекс Доу Джонса определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются каждые полчаса, и ежедневно публикуется их значение на момент закрытия биржи. Групповые индексы определяются по ценам акций 3- промышленных, 20 транспортных и 15 компаний сферы услуг. Общий индекс рассчитывается по всем 65 компаниям. Их перечень был составлен в 1928 году. В качестве базисного выбран 1920 год. Первоначальная методика исчисления индекса была разработана основателем и редактором крупнейшей в США газеты «Уолл-стрит джорнел» Чарльзом Доу.

Индекс Стэндарда и Пура – индекс, рассчитываемый по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи как средний взвешенный показатель, учитывающий общее число выпущенных компаний акций. В число компаний, акции которых включены в индекс, входят 400 промышленных корпораций, 40 - финансовых, 20 - транспортных и 40 - сферы услуг.

Системы индексов

Выбор базы и весов индексов – это два важнейших вопроса построения системы индексов.

Опр.8.Система индексов – это ряд последовательно построенных индексов. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.

Опр.9.Система базисных индексов – это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода.

Опр.10.Система цепных индексов – это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения.

Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные – четче отражают последовательность изменения уровней во времени.

Замечание.1.: Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы.

Замечание.2.: Если известны последовательные значения базисных индексов, легко рассчитать на их основе цепные индексы.

При построении систем индексов можно использовать постоянные и переменные веса.

Опр.11.Системой индексов с постоянными весами называется система сводных индексов одного и того же явления, вычисленных с весами, не меняющимися при переходе от одного индекса к другому. Это позволяет исключить влияние изменения структуры на величину индекса.

Опр.12.Система индексов с переменными весами представляет собой систему сводных индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного к другому. Переменные веса – это веса отчетного периода.

Самостоятельно доказать замечания:

Зная базисные индексы, можно рассчитать цепные;

При наличии цепных индексов легко получить соответствующие им базисные индексы.

Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за “n” периодов:

1.Цепные индексы цен с переменными весами:

2.Цепные индексы цен с постоянными весами:

3.Базисные индексы цен с переменными весами:

4.Базисные индексы цен с постоянными весами: