Питання для самоперевірки.

1. Що називається кулісою? Наведіть приклади.

2. Коли виникає прискорення Коріоліса, як визначити його модуль та напрямок?

3. З яких складових складається швидкість та прискорення кулісного каменю?

18 Самостійна робота №17

Тема: Зрівноваження ланок механізмів

Питання, що розглядаються

1. Зрівноваження обертових мас

2. Зрівноваження плоских механізмів методом замінюючи мас

3. Розв’’язання задачі.

В механізмах при русі ланок виникають сили інерції, яки, як правило носять шкідливий характер, додатково навантажуючи фундаменти верстатів, рами та корпуси механізмів.

Не зрівноваженість механізмів призводить до появи додаткових сил інерції, які впливають на міцність механізмів та їх елементів.

Механізм вважається повністю зрівноваженим, коли головний вектор сил інерції Рі та головний момент інерції Мі дорівнюють нулю.

Якщо зрівноважити лише головний вектор сил інерції, то такий механізм називають статично зрівноваженим. Якщо до цього ще і головний момент сил інерції зрівноважити, то механізму буде зрівноваженим як статично, так і динамічно (моментне).

Статичне балансування виконують для плоских важільних механізмів та деталей типу маховик, диск, та інших, коли діаметр значно більше товщини деталі. Дослідним шляхом визначають додаткові маси (противаги), які закріплюються на деталях та усовують вплив сил інерції.

Динамічне балансування важливо виконувати для деталей типу вал, ротор та інших деталей, довжина яких значно більше діаметру. В цьому випадку задачею балансування е встановлення двох додаткових мас, які зрівноважують головний вектор і головний момент сил інерції.

Кривошипно-шатунні механізми сучасних двигунів машин зрівноважено як статично, так і динамічно.

Для зрівноваження плоских механізмів застосовують метод замініючих мас. Сутність метода полягає в тому, що кожна ланка механізму замінюється двома зосередженими масами, після чого встановлюються корегуючи маси та об’єднуються із заміняючи ми масами так, щоб об’єднані маси розташувалися би у кінцевому рахунку в нерухомих точках механізму.

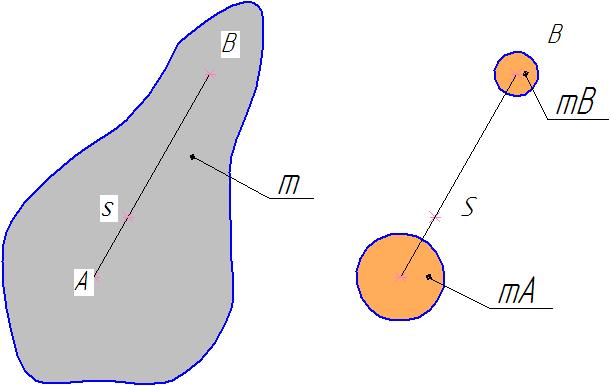
Рисунок 1- До визначення замінних мас

Нехай тіло масою m здійснює плоский або обертовий рух. Зосередимо масу тіла в двох точках А і В. Причому значення зосереджених мас m_A i m_B знаходимо з рівнянь:

Тобто маса системи, що замінює задане тіло дорівнює його масі, а центр мас системи співпадає з центром мас реального тіла. Звідси випливає, що головний вектор сил інерції системи, що замінює реальне тіло, дорівнює головному вектору сил інерції цього тіла.

Приклад. Необхідно статично зрівноважити горизонтальний кривошипно-повзунний механізм таким чином, щоб усунути динамічний вплив на основу (фундамент) у вертикальному напрямку. m₁=4кг, m₂=10кг, m₃=2кг, ,

Рисунок 2- схема кривошипно-повзунного механізму

Замінюємо ланки заданого механізму зосередженими масами.

Для ланки 1:

Схема розміщення розрахованих замінюючи мас наведена на рисунку 3.

Рисунок 3–Схема розміщення замінюючи мас для ланки 1

Далі розраховуємо замінюючи маси для ланки 3 (шатун):

Рисунок 4–Схема розміщення замінюючи мас для ланки 2

Таким чином, в точці А зосереджена маса

В точці В зосереджена маса

Розташовуємо на ланці 1 противагу з таким розрахунком, щоб центр ваги системи мас та співпав з нерухомою точкою О механізму:

,

де h=100мм-плече, яке обираємо з конструктивних міркувань.

Тоді маси необхідної противаги:

Схема механізму з противагою зображена на рисунку 5.

Рисунок 5 - Схема механізму з противагою

Об’єднуємо маси, яки розміщені на ланці 1в нерухомій точці О. Таким чином, після розташування противаги заданий механізм може бути заміненим системою лише двох мас: нерухомою масою та горизонтально рухомою масою і центр ваги механізму буде рухатися лише горизонтально, внаслідок чого динамічна складова сил інерції на фундамент буде дорівнювати нулю. Схема механізму у вигляді системи двох мас наведена на рисунку 6.

Рисунок 6 - Схема механізму з двома масами

Задача. Для кривошипно-повзунного механізму дано m₂, , , , (рисунок 1) розрахувати статичні замінюючи маси та шатуна. Визначити масу противаги для зрівноваження маси . Плече для встановлення противаги вибрати довільно з умови . Виконати схему механізму та схему замінюючи мас.

Таблиця 1- Вихідні дані

Варіант	ω1, с-1	m2, кг	LOA, мм	LAB, мм	LAS2, мм
1	100	50	350	1500	500
2	140	30	370	1600	550
3	130	40	380	1800	600
4	120	20	400	2000	700
5	145	10	450	2200	700
6	150	15	440	2200	750
7	130	42	250	1300	400
8	110	35	360	1200	300
9	90	24	400	1600	400
10	160	16	200	1000	300

Питання для самоконтролю

1. Поясніть причину виникнення сил інерції в ланках механізму

2. Як розрахувати силу інерції при

А) нерівномірному прямолінійному русі

Б) нерівномірному криволінійному русі

3) Яки є види балансування деталей, що здійснюють обертовий рух?

4) В чому полягає метод замінюючи мас і для яких видів механізмів його застосовують?

Додаток 1

Площі, координати центру ваги, осьові моменти інерції, моменти опору і радіуси інерції деяких плоских фігур

Форма поперечного перерізу	Площа, см2	Осьовий момент інерції, см4	Момент опору, см3	Радіус інерції, см
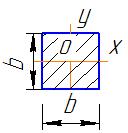
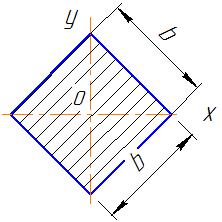
квадрат
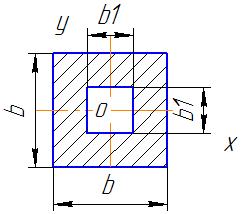
Полий квадрат
Полий тонкостінний квадрат
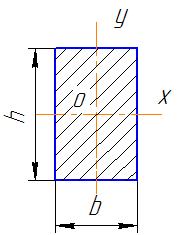
Прямокутник

Форма поперечного перерізу	Площа, см2	Осьовий момент інерції, см4	Момент опору, см3	Радіус інерції, см
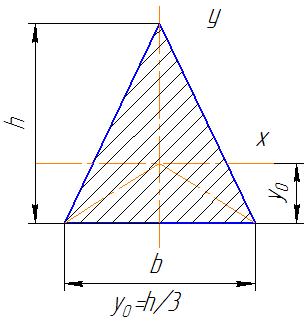
Трикутник			у вершині у основи
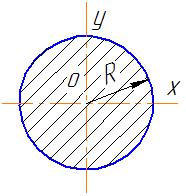
Коло
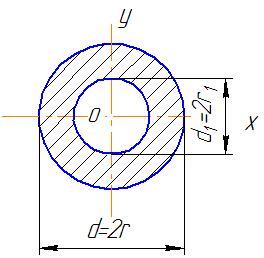
Кільце
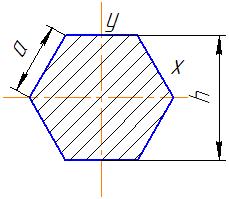
Правильний шестикутник	або	або

Додаток 2