18.2. Определение предельного состояния системы при растяжениисжатии

 

Для статически определимой системы, в элементах которой возникают лишь продольные усилия, расчеты на прочность по допускаемым напряжениям и по предельным нагрузкам дают один и тот же результат. Результаты аналогичных расчетов статически неопределимой системы различны.

В качестве примера рассмотрим систему, представляющую со­бой абсолютно жесткую балку, с одним концом шарнирно опертую, и подвешенную на трех одинаковых идеально упругопластических подвесках, длиной l, площадью поперечного сечения F, модулем упругости материала Е, при заданной схеме нагружения силой Р (рис.18.1, а). Заданная система дважды статически неопределима.

По мере роста силы P, подвески 1, 2, 3 поэтапно будут пере­ходить в пластическое состояние, причем напряжения в каждой подвеске не могут превышать  .

Выделим следующие стадии деформирования заданной систе­мы.

Первая стадия: все подвески работают упруго. Для опре­деления реакций в подвесках составляем уравнения равновесия:

.                                                                           (18.1)

Для определения величин усилий в подвесках N₁, N₂ и N₃ не­обходимо составить еще два уравнения совместности. Учитывая, что балка абсолютно жесткая и деформации в подвесках пропор­циональны возникающим в них усилиям, то из условия подобия треугольников ADD', ACC' и ABB' (рис.18.1), имеем:

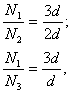
откуда

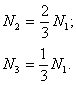                                                                                                                     (18.2)

Тогда из (18.1) с учетом (18.2) опре­деляются реакции во всех подвесках:

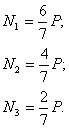                                                                                                                       (18.3)

Вторая ста­дия: при некото­ром значении P, как это следует из (18.3), сначала наи­более нагруженная первая подвеска, переходит в пластическое состояние, то есть   (рис.18.1, б). При этом из (18.2) можно установить, что в остальных подвесках усилия будут равны:

;    .                                                                                          (18.4)

Подставляя значения усилий в уравнение равновесия (18.1), по­лучим:

,

откуда и определим величину внешней силы Р, при котором систе­ма переходит во второе состояние:

.                                                                                                                         (18.5)

Рис.18.1

 

Третья стадия: при дальнейшем росте значения силы P, как это следует из (18.3), и вторая подвеска переходит в пластическое состояние, то есть N₁ = N₂ =   (рис.18.1, в). При этом, из третьего со­отношения (18.3), значение усилия в третьей подвеске будет равно:

.                                                                                                                 (18.6)

Из уравнения равновесия (18.1), с учетом значения усилий в подвесках в третьем состоянии, получим:

.                                                                                                                                   (18.7)

Четвертая стадия  предельное состояние: в этом состоянии усилия во всех трех подвесках равны своему предель­ному значению, т.е.   (рис.18.1, г). Уравнение равновесия (18.1), при этом принимает вид:

,                                                                                    (18.8)

откуда и определяется предельная величина внешней силы:

.                                                                                                                 (18.9)

Далее определим перемещение f_i балки в точке приложения внешней силы P в различных стадиях работы заданной системы.

При переходе заданной системы от первого стадии деформиро­вания ко второму, имеем:

;     .

При переходе заданной системы от второй стадии к третьей, имеем:

;     .

И наконец, при переходе системы от третьей стадии к пре­дельному состоянию, получим:

.

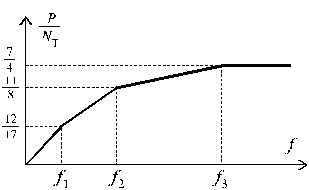
Рис.18.2

               

Зависимость f от P показана на рис.18.2. Она изображается ло­маной линией, которая после предельного равновесного состояния становится горизонтальной, то есть после того, как напряжения достигнут предела текучести во всех трех подвесках. Откуда следует, что при постоянной  , пе­ремещение f  беспредельно возрас­тает, т.е. происходит разрушение системы.

Как видно из приведенного примера, расчет даже для такой простой системы оказывается до­вольно громоздким, хотя он дает возможность находить не только предельную силу, но и описать поведение конструкции в процес­се ее нагружения. На практике, при расчете систем с учетом плас­тических деформаций рассматривают только предельное состояние.