5 Построение плана ускорений
Ускорение точки A определяем с уравнения
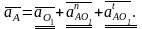
где аO1 – ускорение точки O1=0, так как она неподвижна;
нормальное
ускорение точки A. Его величина
тангенциальное
ускорение точки A=0, так как ε1=0.
Выбираем положение точки Ра – полюс и проводим вектор нормального ускорения точки A.
Масштабный коэффициент плана ускорений:
Ускорение точки B определяем с системы уравнений
где
кориолюсово ускорение точки B. Его
направление определяет направление
оборота угловой скорости ω3.
Что бы определить направление кориолюсового
ускорения необходимо вектор скорости
BA повернуть в направлении обороту
угловой скорости ω3
на 900
.
Величина ускорения равна
релятивное
ускорение точки B которое известно по
направлению;
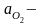ускорение
точки O2=0,
так как она неподвижна;
нормальное
ускорение B, которое равно
тангенциальное
ускорение точки
B, которое известно по направлению;
Определяем длины векторов ускорений
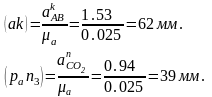
Графически решаем данную систему и определяем ускорения
Отрезок
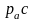определяем
из пропорции:
Ускорение точки С составляет
Ускорение тоски D определяем из системы уравнений
где
нормальное
ускорение точки D, которое равно
кориолюсово
ускорение точки D, которое равно 0, так
як w5=0.
Определяем длину вектора нормального ускорения
Графически решаем данную систему и определяем ускорения
Определяем тангенциальные кладовые:
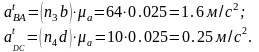
Угловые ускорения
6 Аналитический анализ механизма
Целью
аналитического анализа рычажного
механизма является составление уравнений
геометрического анализа, решение их,
выделение побочных и основных решений,
определяющих положения звеньев, а также
исследование функций положения выходных
звеньев структурных групп.
Выделяем в механизме два замкнутых векторных контура. Расчеты ведем для второго положения.
Первый замкнутый контур О2АО1О2
Второй контур О2СD
Рассмотрим первый векторный контур
Запишем векторное уравнение
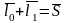(1)
Уравнение (1) спроектируем на оси координат
(2)
Из
системы (2) определяем параметры длины
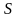и угол
Определяем параметр
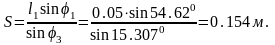
Систему
(2) дифференцируем по обобщенной
координате
и получаем
(3)
где,
и
- аналог угловой скорости звена 3 и аналог
относительной скорости скольжения
звена 3 вдоль оси ползуна 2 соответственно.
Из углов первого и второго уравнения вычитаем угол и получаем
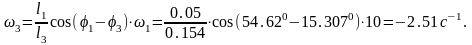
Для определения ускорений звеньев механизма систему (3) дифференцируем по обобщенной координате и получаем
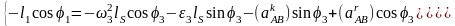(4)
Из системы 4 получаем
Рассмотрим второй векторный контур и запишем векторное уравнение
(5)
Уравнение (5) проектируем на оси координат
(6)
Определяем
угол
Систему (6) дифференцируем по обобщенной координате и получаем
(7)
где,
и
- аналог угловой скорости звена 4 и аналог
скорости ползуна 5 соответственно.
Для определения ускорений звеньев механизма систему (7) дифференцируем по обобщенной координате и получаем
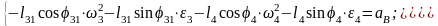
Определим координаты центров масс.
=
k1
=
k2
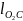
Найдем аналоги скоростей для центров масс.
После дифференцирования уравнений (13) и (16) получаем:
