Поступательное движение

ВВЕДЕНИЕ

Изучение курса общей физики имеет своей целью представление физической теории как обобщение наблюдений, практического опыта и эксперимента. Поэтому курс общей физики, с одной стороны, должен представлять собой физическую теорию в адекватной математической форме, а со другой - этот курс должен быть экспериментальным и должен знакомить студентов с основными методиками экспериментальных исследований, главными методами измерения физических величин, простейшими методами обработки результатов эксперимента и основными физическими приборами. Курс общей физики должны сформулировать у студентов определенные привычки экспериментальной работы, научить правильно выражать физическую идею, количественно формулировать и решать физические задачи, оценивать порядок физических величин, которые исследуются.

Выполнению этих задач в значительной мере служат лабораторные работы. Для их качественного(а, значит, эффективного для обучения) выполнение необходимо понимать содержание исследуемого явления. Тому преподаванию, содержания и методике выполнения лабораторных работ должны предшествовать небольшое вступление, которое содержит общий взгляд на способы решения соответствующих задач. Наиболее наглядно это видно на примере механики.

Классическая механика - наука о законах движения и равновесия макроскопических материальных тел. При этом под механическим движением понимается простейшая форма движения - изменение положений тел относительно друг друга с течением времени.

Движение тело определено, если известный закон его движения, т.е. закон, по которому изменяется положение тела в просторные с течением времени. При этом в механике используются определенная модель пространства и времени, а также система отсчета.

Кинематика - это раздел механики, где изучаются способы описания движения в выбранной системе отсчета независимо от причин, которые его предопределяют.

Траекторией точки называется геометрическое место последовательных положений тела в выбранной системе отсчета.

Законы движения точки могут задаваться:

а) в векторной форме:

; (1)

б) в координатной форме:

в декартовой системе координат

(2)

в криволинейных координатах

; (3)

в) в натуральной форме задается траектория точки и закон движения точки вдоль траектории

, (4)

где - дуга траектории

.

Соотношение (1), (2) представляют собой параметрическое уравнение траектории, где - параметр. Вид траектории определяет геометрический характер движения: прямолинейный, круговой, плоский, пространственный.

Знавая закон движения , можно найти скорость и ускорения :

;

. (6)

Обратная задача кинематики заключается в нахождении и при известном .

Для решения такой задачи необходимо еще знать так называемые начальные условия, а именно скорость и положения в некоторый начальный момент времени .

Например, при , скорость и положения точки определяются формулами

. (7)

Следующий шаг описания механического движения - рассмотрение взаимодействия между материальными точками. Классическая механика выходит из идеи дальнодії: действие в просторные передается мгновенно. Это действие характеризуется силой; сила вызывает ускорение. Основная задача механики заключается в динамическом описании движения, которое устанавливает связь между силой и кинематическим уравнением движения.

Классическая механика базируется на трех основных законах, которые называются законами Ньютона и которые можно сформулировать таким образом.

1. Первый закон - закон инерции.

В природе существуют системы отсчета, в которых изолированная (т.е. невзаимодействующая ни с какими материальными объектами) материальная точка находится в состоянии покоя или равномерного прямолинейного движения. Такие системы называются инерциальными. Закон инерции называют также первым законом Ньютона.

2. Второй закон Ньютона.

Если на материальную точку действует сила , то точка получает по отношению к инерциальной системы отсчета такое ускорение , что произведение массы точки на это ускорение равняется силе:

. (8)

В этом законе масса представляет себе меру инертности тела, т.е. свойства разных тел по разному реагировать на действие одной и той же силы. Подчеркнем, что закон (8) одновременно определяет силу, как векторную величину, которая характеризует действие на тело других тел, в результате чего тело получает ускорение или деформируется.

3. Третий закон Ньютона.

Две материальные точки действуют одна на одну силами, одинаковыми по абсолютной величине и направленными в противоположных направлениях вдоль прямой, которая соединяет эти точки.

К основным законам динамики относят еще и закон независимости действия сил, согласно которому при одновременном действии на материальную точку нескольких сил, каждая из них придает точке такое же ускорение, которое бы она придавала, действуя только одна - принцип суперпозиции сил:

. (9)

Для того, чтобы свести нахождение закона движения к чисто математической задаче, необходимо прежде всего (в соответствии с (8)) знать законы действующих на тело сил. Каждый такой закон получен на основе обработки и обобщения исследовательских данных и по сущности, всегда строится на уравнении (8) как на определении силы.

Приведем примеры этих сил в самом простом виде, когда взаимодействуя тела (заряды) находятся в покое или двигаются с малыми (нерелятивистскими) скоростями.

1. Сила гравитационного притяжения.

,

2. Однородная сила тяготения.

,

- ускорение в поле тяготения

3. Кулоновская сила взаимодействия электрических зарядов.

,

4. Сила упругости

- положительный коэффициент упругости.

5. Сила сопротивления (жидкое трение)

- скорость тела относительно сплошной среды (жидкости или газа), - коэффициент сопротивления.

6. Сила трения скольжения

- коэффициент трения скольжения, - сила нормального давления, сила направлена в сторону, противоположную направлению движения тела.

В общем случае сила зависит от времени, координат и скорости тела.

Основное уравнение динамики представляет собой математическое выражение второго закона Ньютона

, (10)

Или в координатном виде:

. (11)

По своей сути эти уравнения представляют собой систему дифференционных уравнений второго порядка.

Во всех инерциальных системах отсчета, например, в условно недвижимой и такой, что двигается относительно нее вдоль оси равномерно и прямолинейно со скоростью , второй закон Ньютона имеет одинаковый вид. Инвариантность уравнения движения относительно преобразований Галилея

представляет собой принцип относительности Галилея.

В динамике решаются две основных задачи:

1.Найти действующую на тело силу , если известные его масса и закон движения . В этом случае задача приводится к диферинцирование по времени.

2. Найти закон движения тела , если известные и . В этом случае необходимо задать начальные условия – скорость и положения тела в начальный момент времени. Эта задача приводится к интегрированию уравнений (10), (11). Аналитически начальные условия записываются таким образом (при решении задачи в декартовой системе координат):

. (11а)

Наличие начальных условий разрешает найти единственно возможные решения задачи (10) - (11а) при заданных силах, это и будут искомые кинематические уравнения движения:

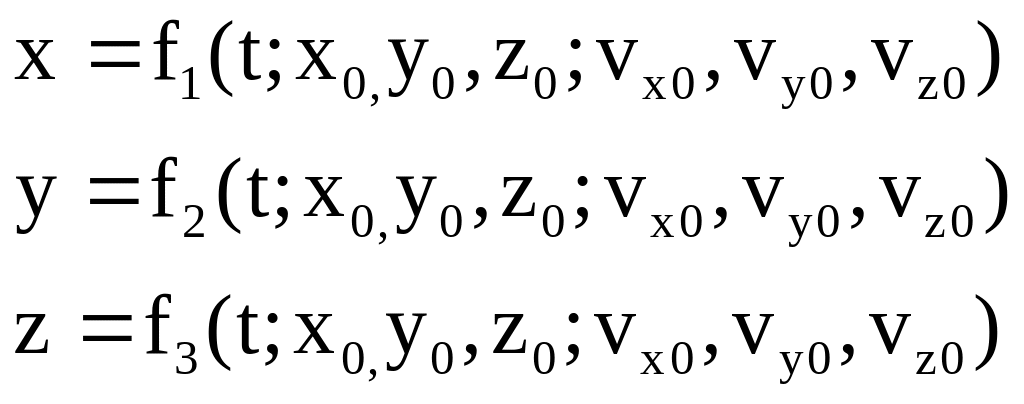. (11б)

Отметим, что уравнение (11) имеют универсальный характер и справедливые для всего бесконечного многообразия механических задач. Каждая конкретная задача характеризуется задачам определенных сил и начальных условий.

Таким образом, вторая задача динамики может быть разрешима полностью. Однако в большинстве случаев, дифференциальные уравнения движения не могут быть разрешины аналитически (т.е. доведены до интегралов) и не может быть получено точное решение задачи. Для практики это не имеет решающего значения, поскольку приближенное решение можно получить с помощью ЭВМ.

Уравнение (11б) означают, что состояние системы тел в некоторый момент времени единственно определяется их взаимодействием (т.е. силами) и начальными условиями. Другими словами, все следующие состояния обусловленные предыдущим. Это положение носит название принципа механического детерминизма.

Обратим внимание на оборотность механических процессов. В простейшем случае силы, которые действуют на тело, зависят только от положения тела . Если при этом в уравнении (11) обернуть время, т.е. сделать замену , то

При этом и уравнение (11) не изменяется, т.е. оно есть инвариантном относительно обращения времени.

Относительно скорости движения, то

При обращении времени направление скорости изменяется на противоположное. Таким образом, оборотность механических процессов означает, что когда существует некоторое движение, то возможный и обратной движение, при котором система проходит все те же положения в просторные в обратной последовательности с противоположной за направлением скоростью.

В частности в случае одномерного движения, ось координат вдоль траектории, получим только одно дифференциальное уравнение движения:

(12)

и начальные условия:

.

Решение этого уравнения в некоторых случаях можно свести к интегралам.

Рассмотрим примеры.

а) Одноизмеримое движение под действием постоянной силы .

Его общий интеграл получается по методу распределения переменных и выражается такой формулой равноускоренного движения

б) Сила – функция времени .

Простыми приемами решения приходится к первым и вторым интегралам.

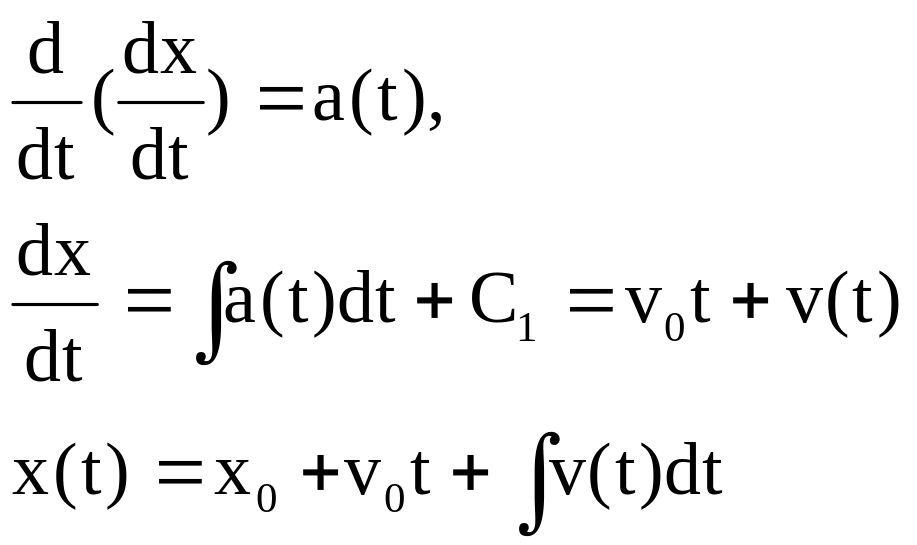
в) Сила зависит от координаты .

Делаем подстановку . Тогда

и это уравнение принимает вид

Его решение

Поскольку , то

После разделения переменных можно записать:

.

2) Сила зависит от скорости .

Разделив переменные, получим

.

Переобозначив , имеем

.

Дальше запишем исходное уравнение в виде

.

Разделив переменные,

и переобозначив , имеем

.

Исключив из уравнений для и величину , найдем как функцию .

Кроме дифференциальных уравнений движения для решения задач динамики широко используются так называемые общие теоремы динамики, которые являются первыми интегралами уравнений движения.

К ним, в частности, относятся:

1.Теорема об изменении импульса системы.

Импульс системы тел , где – импульс –го тела. Изменение импульса системы за произвольный промежуток времени равняется геометрической сумме импульсов, действующих на систему внешних сил за тот же промежуток времени

(13)

Из этой теоремы вытекает закон сохранения импульса: если геометрическая сумма всех действующих на систему внешних сил равняется нулю, то импульс системы остается неизменным. Теорема используется при изучении движения жидкостей, в теории столкновенья, в теории реактивного движения и др. Следствием этой теории есть также теорема о движении центра масс: центр масс механической системы двигается как материальная точка, масса которой равняется массе системы и на которую действуют все внешние силы, приложенные к системе.

2. Теорема об изменении кинетической энергии системы.

Изменение кинетической энергии системы при дорогому ии перемещении равняется сумме работ всех приложенных сил на этом перемещении:

(14).

В случае, когда все действующие силы потенциальные, из теоремы вытекает закон сохранения механической энергии: при движению под действием потенциальных сил сумма кинетической и потенциальной энергии системы остается неизменной величиной.