Работа №13 Вынужденные колебания. Резонанс

Цель работы: снять амплитудные резонансные кривые в средах, которые характеризуются разными коэффициентами вязкости, рассчитать для каждого случая добротность системы, коэффициент затухания, логарифмический декремент затухания; провести анализ полученных данных.

Теоретический материал.

Затухающие колебания. Уравнение колебаний при наличии трения. Частота и логарифмический декремент затухания. Время релаксации. Апериодические движения. Вынужденные колебания. Уравнение колебаний под действием вынуждающей силы. Резонанс. Амплитудные и фазовые резонансные кривые. Добротность. Получение резонансной кривой и ее связь с добротностью.

Рассмотрим сначала свободные колебания. Если телу предоставить запас энергии и дать возможность совершать колебания, то при малых углах отклонения и малой силе трения оно будет колебаться почти по гармоническому закону с собственной частотой . Здесь - масса тела, - коэффициент упругости. Но в реальных условиях предоставленный телу запас энергии уменьшается. Энергия тратится на работу против сил трения. В случае малых отклонений тела от положения равновесия силу трения можно принять пропорциональной скорости его движения и уравнение движения тела будет

, (1)

а его решение

. (2)

Здесь - смещение тела относительно положения равновесия, - коэффициент силы трения, - начальные амплитуды и фаза колебаний,

. (3)

Коэффициент затухания характеризует скорость затухания амплитуды колебаний со временем. Если взять отношение амплитуд в (2) через промежуток времени , то оно будет равняться . Таким образом, коэффициент затухания  - величина обратная промежутку времени , на протяжении которого амплитуда колебаний тела уменьшается в e раз.

Для тела, которое колеблется, более естественной является характеристика не по времени, а по числу колебаний. Поэтому вводят еще одну величину – логарифмический декремент затухания , который показывает уменьшение амплитуды за один период. Чтобы определить смысл , обозначим через N число колебаний, на протяжении которых амплитуда колебаний уменьшается в е раз. Тогда можно записать, что и . Таким бразом, логарифмический декремент затухания  ‑ величина ,обратная числу колебаний, после которых амплитуда уменьшается в е раз.

Для примера характеристик  и  сравним скорость затухания двух систем с параметрами:

и

Как видно, колебание первой системы быстрее затухают по времени, а второй - по числу колебаний.

В технике вместо логарифмического декремента вводят величину, которую называют добротностью

(4)

Добротность тем больше, чем дольше длится колебание системы, причем здесь слово “дольше” относится к естественному масштабу времени системы, который задается продолжительностью отдельного колебания. В приведенном выше примере добротность второй системы в 100 раз меньше, чем добротность первой системы.

Чтобы колебания не затухали, необходимо подводить энергию. Рассмотрим колебания тела под действием внешней силы, которая изменяется по закону . Такие колебания происходят с частотой внешней силы и носят название вынужденных. Уравнение динамики вынужденных колебаний имеет вид

.

Решением этого уравнения является функция

, (5)

где

, (6)

(7)

Скорость тела будет изменяться по закону

, (8)

Функция (5) описывает установившиеся колебания, при которых энергия, которая поступает от внешнего источника, полностью тратится на работу против сил трения. Из соотношений (5-7) не сложно получить, что энергия сильно зависит от значений частоты  и значений . Действительно, работа, которая выполняется внешней силой за период колебаний

(9).

Как видно из (9), работа будет максимальна при значении , т.е. когда фаза скорости совпадает с фазой внешней силы. Из (7) видно, что такому значению  отвечает частота

, (10)

и значением максимальной амплитуды смещения установившихся колебаний при малом по сравнению с собственной частотой колебаний коэффициенте трения будет резонансная амплитуда

. (11)

Резонанс скорости будет наблюдаться, когда внешняя частота  совпадает з .

Если частоту  плавно изменять, то согласно (6) и (7) получим зависимости и скорости , которые можно изобразить графически резонансными кривыми(рис. 4-6).

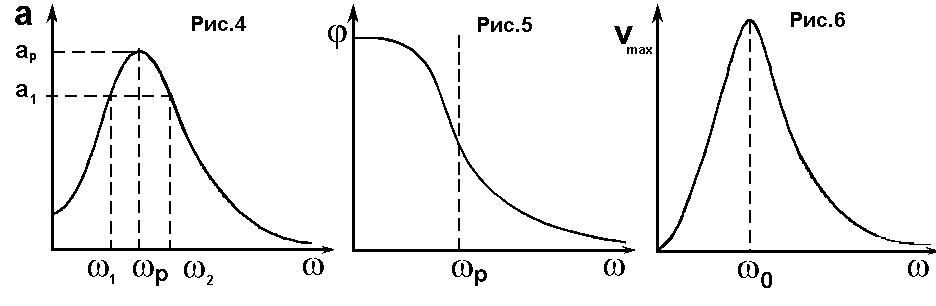
Таким образом, результат действия одного осциллятора с частотой  на второй с собственной частотой сильно зависит от соотношения частот. При частоте система колеблется с максимальной амплитудой , т.е. осциллятор с собственной частотой принимает максимум энергии от внешнего источника. Это явление называют резонансом смещения системы, которая колеблется. Как нетрудно проследить из (8), резонанс скорости движения тела наблюдается, когда частота внешней силы .

Не следует забывать, что резонансные кривые (рис. 4-6) относятся к установившимся (стационарным) колебаниям. Стационарные колебания устанавливаются не сразу, а спустя некоторое время. Чем острее резонансная кривая, тем дольше надо ждать установления стационарной амплитуды.

Острота резонансной кривой можно охарактеризовать добротностью осциллятора. Добротность осциллятора Q определяют как отношение энергии, которой он обладает при резонансе, к энергии, которая тратится на работу против сил трения на протяжении одного периода колебаний. Если взять это отношение, то после подсчетов получим выражение (4).

Добротность осциллятора связана с шириной резонансной кривой 2. Ширина резонансной кривой выделяет область тех частот внешней вынужденной силы, для которых энергия колебаний осциллятора составляет не меньше 50% от энергии колебаний при резонансе. Так как энергия осцилятора пропорциональна , то ширину резонансной кривой на рис.4 можно получить, если провести прямую, параллельную оси абсцисс через ординату a₁, равную . Точки пересечения этой прямой с резонансной кривой выделяют область частот . Величину называют полушириною резонансной кривой. Ведь и - частоты внешнего действия, при которых отношение

(12)

Если коэффициент затухания мал , то резонансная кривая достаточно симметрична в области резонанса. В этом случае, если подставить из (11) и из (6) для в (12), то получим, что и добротность

, (13)

Из соотношение (13) видно, что добротность осциллятора характеризует как частоту резонансной кривой, так и время установления колебаний (Q зависит от ). Чем острее резонансная кривая, тем больше время установления стационарных вынужденных колебаний.

Описание установки и методики измерений.

В данной работе необходимо измерить амплитуды колебаний тела при разных частотах действующего внешнего осциллятора. Построить кривую и определить ширину кривой, коэффициент затуханий , декремент затуханий  и добротность Q.

Металлический ферромагнитный тонкий стержень жестко закрепляется на массивном штативе так, чтобы точку закрепления можно было изменять. Вблизи этого стержня расположен электромагнит, который действует на него с некоторой силой, изменяющейся по периодическому закону. Электромагнит питается от звукового генератора. Это позволяет изменять частоту и амплитуду силы, которая действует на стержень, путем изменения напряжения на выходе генератора. Амплитуду колебаний стержня можно измерить с помощью микроскопа типа “Мир”, в окуляре которого размещена шкала с делениями.

Порядок выполнения работы:

1). Включите освещение стержня и проведите юстирование системы так, чтобы изображение стержня было четким и находилось в центре шкалы.

2). Включите генератор и подберите частоту действующей силы, при которой колебание стержня максимальны. Отрегулируйте напряжение на выходе генератора так, чтобы отклонение стержня от положения равновесия не выходили за пределы шкалы. Установленное напряжение не изменяйте на протяжении измерений амплитуды колебаний при разных частотах, так как оно определяет значение .

3). Найдите собственную частоту стержня . Для этого установите частоту генератора на отметке “нуль” и, постепенно увеличивая ее, определите значение амплитуды колебаний стержня на разных частотах. Постройте график и найдите ширину кривой и . Убедитесь, что мало, а кривая острая. Тогда приблизительно можно сравнить з . Если значением нельзя пренебречь, то по формуле (10), т.е.:

Измените точку закрепления стержня и определите для трех разных длин. Сравните эти частоты и сделайте вывод.

4). Выясните влияние вязкости среды на колебание стержня. Для этого при определенной длине стержня и значении F₀ поместите его по череди в жидкости с разным значением коефициента вязкости и определите . Постройте эти зависимости и найдите . При этом в качестве можно взять его значение, определенное из колебаний в воздухе.

Контрольные вопросы:

1. Запишите уравнение движения линейного осциллятора под действием гармонической внешней силы. От чего зависит время установления стационарного режима вынужденных колебаний? Чему равняется частота постоянных вынужденных колебаний при гармоническом внешнем влиянии?

2. Что называется резонансом? Укажите характерные особенности амплитудной резонансной кривой? Какая частота называется резонансной? Как связана резонансная частота ω_рез с частотой собственных колебаний ω₀? В каком случае резонансная частота ω_рез равняется собственной частоте ω₀?

3. Какое соотношение между фазой вынужденных колебаний и фазой внешней силы в следующих случаях: 1) ω << ω₀, 2) ω >> ω₀, 3) ω ≈ ω_0. Чем объяснить, что наиболее эффективная передача энергии от источника внешней силы к колебательной системе происходит при резонансе?

4. Используя уравнение движения вынужденных колебаний и фазовую резонансную кривую, рассмотрите физическую картину вынужденных колебаний в разных областях частот, полагая трение малым, т.е. коэффициент затухания δ << ω₀? Какие силы, входящие в уравнение движения, определяют величину амплитуды вынужденных колебаний в следующих случаях: 1) ω << ω₀, 2) ω >> ω₀, 3) ω ≈ ω₀? Какая сила компенсирует внешнюю силу при резонансе?

5. Что называется коэффициентом затухания (декрементом затухания) - δ и логарифмическим декрементом затухания θ? Какая из этих величин характеризует скорость затухания во времени? Какой величиной оценивают скорость затухания в зависимости от числа колебаний?

6. Что называется добротностью? Почему добротность является важнейшей характеристикой резонансных свойств системы?

7. Объясните, как с помощью амплитудной резонансной кривой определить коэффициент затухания, логарифмический декремент затухания и добротность.