
- •Предисловие
- •Подготовка к выполнению лабораторной работы
- •Порядок выполнения работы
- •Оформление рабочего листа
- •Правила округления при вычислениях
- •Поступательное движение
- •Лабораторная работа №1 Измерение физических величин и определение погрешностей измерений. Линейные измерения.
- •Лабораторная работа №2 Определение модулей упругости растягивания и изгиба
- •Лабораторная работа №3 Изучение второго закона динамики на машине Атвуда
- •В векторной форме
- •В проекции на вертикальную ось
- •Лабораторная работа № 4
- •Порядок выполнения работы
- •Лабораторная работа № 5 определение средней силы соударения двух шаров
- •Удар двух шаров.
- •Определение средней силы соударения двух кулек.
- •Определение скорости шариков при соударении.
- •Время разрядки конденсатора в rc-цепи.
- •Порядок выполнения работы.
- •Динамика вращательного движения твердого тела
- •Основные законы динамики вращательного движения тела.
- •Лабораторная работа № 6 Изучение вращательного движения твердого тела при помощи маятника Обербека
- •Лабораторная работа № 7 Определение скорости пули с помощью крутильно- баллистического маятника.
- •Вычисление погрешностей измерений .
- •Лабораторная работа №8 Определение момента инерции махового колеса и момента силы трения в опоре
- •Экспериментальное определение момента инерции кольца и момента силы трения в опоре.
- •Порядок выполнения работы.
- •Лабораторная работа №9 Определение момента инерции и проверка теоремы Штейнера методом крутильных колебаний
- •Порядок выполнения работы.
- •Лабораторная работа №10 Изучение динамики плоского движения с помощью маятнике Максвелла
- •Лабораторная работа № 11 Изучение движения гироскопа
- •Э лементарные сведения о гироскопах
- •Измерения и обработка результатов.
- •Колебательные движения
- •Изучение физического маятника и определение ускорения силы тяготения
- •Работа №13 Вынужденные колебания. Резонанс
- •Работа №14 Определение скорости распространения звука методом интерференции волн
- •Робота№15 Определение скорости распространения звука в воздухе методом сдвига фаз
- •Описание установки и методика измерений.
- •Работа №16 Определение скорости звуковой волны методом резонанса. Образование стоячей волны
- •Работа 17 Изучение колебаний струны и градуировка шкалы частот звукового генератора
- •Приложение
- •2. Фундаментальные физические константы
- •3. Некоторые постоянные числа и приближенные формулы
- •4. Греческий алфавит
- •5. Плотности веществ
- •6. Постоянные газов
Лабораторная работа № 11 Изучение движения гироскопа
Цель работы: ознакомление с особенностями движения гироскопа. Измерение угловой скорости прецессии.
Теоретический материал.
Вращательное движение твердого тела. Момент силы. Момент инерции. Момент импульса твердого тела относительно оси. Уравнение моментов. Мгновенные оси вращения. Главные оси и главные моменты инерции, их физическое содержание. Гироскопы и их применение. Прецессия гироскопа. Свободный гироскоп и гироскоп на вращающемся диске. Физический пример прецессии.
Э лементарные сведения о гироскопах
Рис.1.
Ч
Рис.2.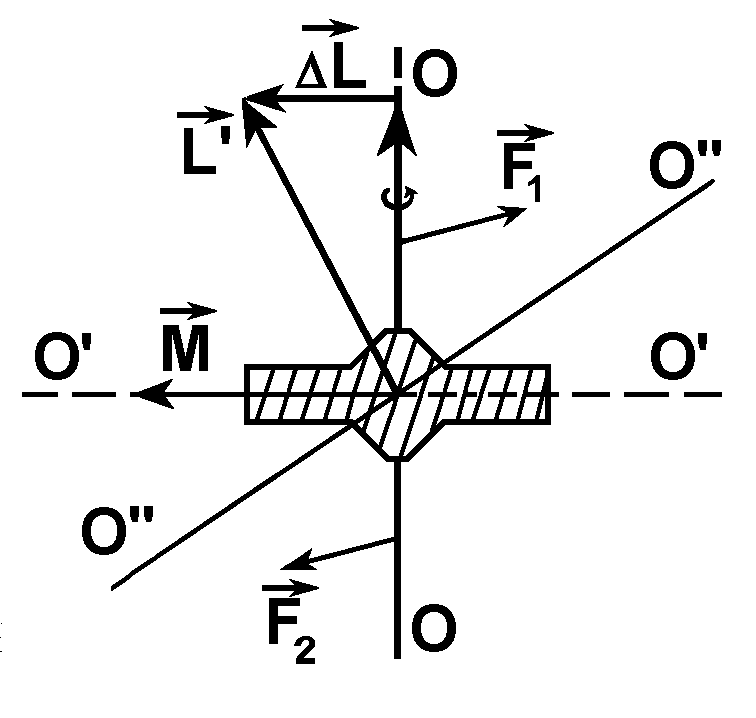
![]() и
и
![]() (рис.
2), которые казалось бы, должны были
вызвать поворот оси гироскопа ОО вокруг
прямой ОБОБ
ось гироскопа вращается вокруг прямой
ОБОБ
(оси ОО, ОБОБ
и ОБОБ
взаимно перпендикулярны). Этот эффект
объясняется законами динамики
вращательного движения. Момент пары
сил
в соответствии с определением направлен
вдоль прямой ОБОБ.
За время
момент импульса
(рис.
2), которые казалось бы, должны были
вызвать поворот оси гироскопа ОО вокруг
прямой ОБОБ
ось гироскопа вращается вокруг прямой
ОБОБ
(оси ОО, ОБОБ
и ОБОБ
взаимно перпендикулярны). Этот эффект
объясняется законами динамики
вращательного движения. Момент пары
сил
в соответствии с определением направлен
вдоль прямой ОБОБ.
За время
момент импульса
![]() ,
получит приращение
,
получит приращение
![]() , (1)
, (1)
т.е.
![]() параллельно
параллельно
![]() .
Итак, через время момент импульса примет
значение
.
Итак, через время момент импульса примет
значение
![]() .
.
Н
Рис.3.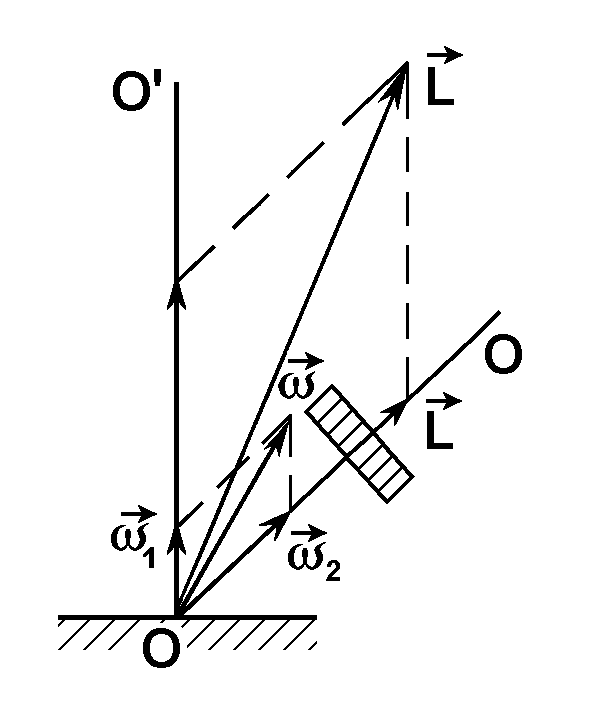
![]() задает новое положение оси вращения
гироскопа и, как легко видеть из рис. 2,
ось обернулась вокруг прямой ОБОБ
так, что угол, между векторами
и
уменьшился. Если действовать на гироскоп
продолжительное время внешними силами,
которые имеют постоянный по направлению
момент
,
ось гироскопа установится, в конечном
итоге, в направлении, которое совпадает
с вектором
.
Это явление положено в основу работы
гироскопического компаса.
задает новое положение оси вращения
гироскопа и, как легко видеть из рис. 2,
ось обернулась вокруг прямой ОБОБ
так, что угол, между векторами
и
уменьшился. Если действовать на гироскоп
продолжительное время внешними силами,
которые имеют постоянный по направлению
момент
,
ось гироскопа установится, в конечном
итоге, в направлении, которое совпадает
с вектором
.
Это явление положено в основу работы
гироскопического компаса.
До
сих пор мы рассматривали простое движение
гироскопа вокруг оси симметрии. Реальный
гироскоп, как правило, принимает участие
в более сложном движении, при котором
вектор момента импульса
может не совпадать с вектором угловой
скорости
![]() .
Рассмотрим частный случай движения
тела, у которого закреплена одна точка
(т. ОБ, рис. 3). Положим, что гироскоп
вращается с угловой скоростью
.
Рассмотрим частный случай движения
тела, у которого закреплена одна точка
(т. ОБ, рис. 3). Положим, что гироскоп
вращается с угловой скоростью
![]() вокруг оси ОО и одновременно ось ОО
вращается вокруг оси ОО
с угловой скоростью
вокруг оси ОО и одновременно ось ОО
вращается вокруг оси ОО
с угловой скоростью
![]() .
Это движение можно заменить вращением
с угловой скоростью
.
Это движение можно заменить вращением
с угловой скоростью
![]() вокруг мгновенной оси, положение которой
определяется вектором
.
Компоненты момента импульса
,
которыми владеет гироскоп при вращении
осей ОО и ОО,
определяются соотношениями:
вокруг мгновенной оси, положение которой
определяется вектором
.
Компоненты момента импульса
,
которыми владеет гироскоп при вращении
осей ОО и ОО,
определяются соотношениями:
![]() ;
;
![]() ,
,
где
![]() и
и![]() - моменты инерции относительно осей ОО
и ОО.
Тогда вектор
будет равен
- моменты инерции относительно осей ОО
и ОО.
Тогда вектор
будет равен
![]() .
.
Легко заметить, что при векторы и не совпадают по направлению.
К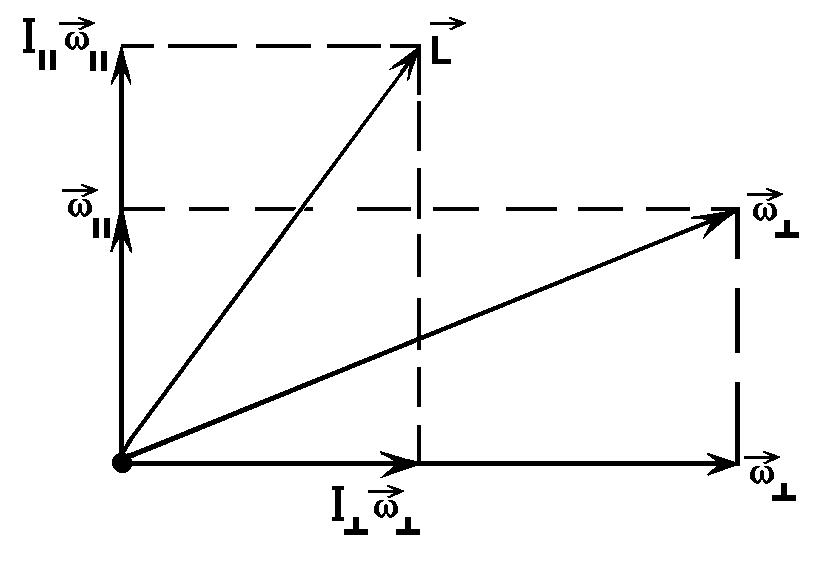 аналогичному результату можно прийти,
если рассмотреть вращение гироскопа
вокруг мгновенной оси, которая не
совпадает с осью симметрии (см. рис. 4).
В этом случае можно разложить вектор
на две составляющие: направленную вдоль
оси фигуры гироскопа
аналогичному результату можно прийти,
если рассмотреть вращение гироскопа
вокруг мгновенной оси, которая не
совпадает с осью симметрии (см. рис. 4).
В этом случае можно разложить вектор
на две составляющие: направленную вдоль
оси фигуры гироскопа
![]() и перпендикулярную к ней
и перпендикулярную к ней
![]() .
В результате получаем:
.
В результате получаем:
![]() , (2)
, (2)
где
![]() и
и
![]() -
моменты инерции относительно указанных
осей. (Очевидно, что направление
и
совпадают лишь в том случае, когда
=
).
-
моменты инерции относительно указанных
осей. (Очевидно, что направление
и
совпадают лишь в том случае, когда
=
).
В основе теории гироскопов лежит уравнение динамики вращательного движения:
![]() . (3)
. (3)
Если момент внешних сил равняется нулю, гироскоп называется свободным. Для свободного гироскопа:
=![]() (4)
(4)
Из уравнения (4) с учетом того, что моменты инерции и не меняются (отсутствуют деформации), следует сохранение во времени компонент и вектора :
![]()
Таким образом, кинетическая энергия вращательного движения гироскопа равно
![]() (5)
(5)
Совокупность уравнений (3)-(5) позволяет объяснить характер движения гироскопа.
У
Рис.5.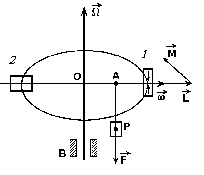 стойчивость
движения быстро вращающегося гироскопа
легко объяснить, исходя из уравнение
(3). Действительно, если гироскоп с большим
моментом инерции привести в быстрое
вращение, то он будет иметь большой
момент импульса. Увеличение момента
за время
стойчивость
движения быстро вращающегося гироскопа
легко объяснить, исходя из уравнение
(3). Действительно, если гироскоп с большим
моментом инерции привести в быстрое
вращение, то он будет иметь большой
момент импульса. Увеличение момента
за время
![]() определяется формулой (3):
определяется формулой (3):
![]() .
.
При
кратковременных влияниях даже больших
сил величина
![]() ,
и направление оси гироскопа практически
не изменяется. Гироскоп как бы
сопротивляется всяким попыткам изменить
величину и направление его момента
импульса.
,
и направление оси гироскопа практически
не изменяется. Гироскоп как бы
сопротивляется всяким попыткам изменить
величину и направление его момента
импульса.
Интересно проявляет себя гироскоп при действии на него внешних сил, момент которых остается постоянным по величине и перпендикулярным к оси обращения. В этом случае наблюдается так называемая вынужденная прецессия гироскопа. Рассмотрим гироскоп, изображенный на рис. 5. Он состоит из маховика 1 и электромотора 2, расположенных на одной оси. Гироскоп устроен так, что он может свободно вращаться вокруг оси симметрии, а также вокруг горизонтальной и вертикальной осей. Приложим к какой-нибудь точке оси гироскопа (т. А) постоянную силу . Если маховик не поворачивается, наблюдается обычное явление: под действием груза P маховик опустится. Однако движение приобретает совсем другой характер, если маховик привести с помощью электромотора в быстрое вращение. В этом случае ось фигуры несбалансированного гироскопа начнет вращаться вокруг вертикальной оси (вынужденная прецессия). Последняя легко объясняется приближенной теорией, в которой предполагается, что угловые скорости возможных движений много меньше угловой скорости вращения гироскопа вокруг оси симметрии. Иначе говоря, в формуле (2) следует учитывать лишь первый член:
![]() (6)
(6)
В таком приближении векторы и параллельны (рис. 4). Поскольку момент силы перпендикулярен оси вращения, а, значит, и к , он не изменяет величину момента импульса, а только изменяет его направление. Итак, если внешняя сила постоянна, то вектор , а с ним и ось гироскопа, должны осуществлять равномерное вращение вокруг вертикальной оси.
Направление
и величину угловой скорости прецессии
легко найти из следующих соображений.
Введем единичный вектор
![]() ,
направленный вдоль оси гироскопа. Длину
отрезка ОА обозначим буквой
.
Тогда момент силы
будет равняется:
,
направленный вдоль оси гироскопа. Длину
отрезка ОА обозначим буквой
.
Тогда момент силы
будет равняется:
![]() ,
так как
,
так как
![]() (7)
(7)
Соответственно избранному направлению вращения маховика векторы и будут направлены вправо, причем
![]() ,
, ![]() (8)
(8)
поскольку
момент импульса
и его производная
![]() взаимно перпендикулярны и не изменяются
по модулю, их можно связать соотношением:
взаимно перпендикулярны и не изменяются
по модулю, их можно связать соотношением:
![]() (9)
(9)
С учетом (3) получаем:
![]()
Принимая во внимание (8), имеем:
![]() откуда
откуда
![]() и.
и.
![]() (10)
(10)
Т
Рис.6.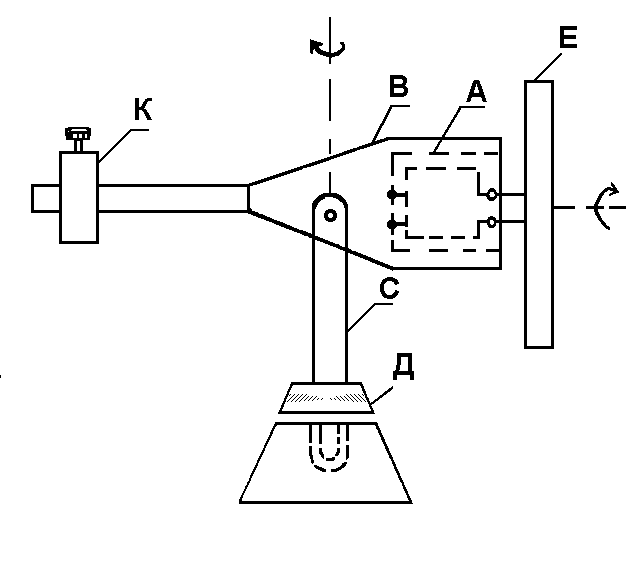
![]() и
антипараллельны,
причем
имеет размерность частоты (проверить
самостоятельно). Эта частота называется
частотой прецессии. Гироскоп будет
осуществлять вращательное движение
вокруг вертикальной оси. Приведенные
соображения справедливы при условии
и
антипараллельны,
причем
имеет размерность частоты (проверить
самостоятельно). Эта частота называется
частотой прецессии. Гироскоп будет
осуществлять вращательное движение
вокруг вертикальной оси. Приведенные
соображения справедливы при условии
![]() .
.
Целью данной работы является ознакомление с особенностями движения гироскопа.
