Лабораторная работа №9 Определение момента инерции и проверка теоремы Штейнера методом крутильных колебаний

Цель работы: методом крутильных колебаний определить момент инерции тел, проверить теорему Штейнера.

Теоретический материал.

В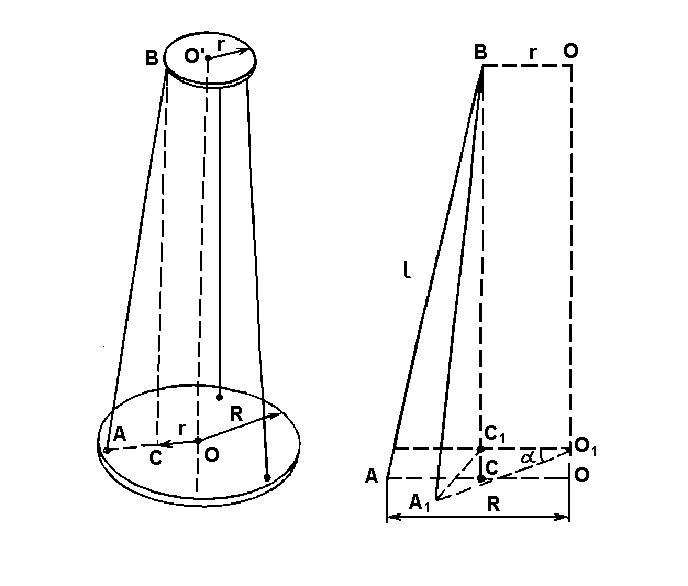 ращательное движение твердого тела. Момент силы, момент инерции. Теорема Штейнера. Момент импульса твердого тела относительно оси. Уравнение движения твердого тела. Уравнение моментов. Системы материальных точек и момент сил, которые действуют на систему материальных точек. Потенциальная и кинетическая энергии. Кинетическая энергия вращающегося твердого тела. Закон сохранения энергии. Консервативные и дисипативні системы. О законах сохранения и неконсервативные системы. Гармонические колебания. Амплитуда, период, частота.

а) б)

рис. 1

Момент инерции тела сложной формы можно измерить методом трифілярного подвеса. Трифілярний подвес представляет собой круглую плоскую платформу, подвешенную на трех, симметрично расположенных металлических нитях (см. рис. 1). Радиус платформы . Верхние концы нитей прикреплены к диску меньшего радиуса . Трифілярний подвес крепится на специальном кронштейне, вмонтированному в стенку.

Платформа может делать крутильные колебания возле вертикальной оси, которая проходит через центры верхнего и нижнего дисков. Колебания возбуждаются поворотом верхнего диска с помощью шнура, связанного с ним и переброшенного через блок.

При крутильных колебаниях платформы центр масс ее перемещается вдоль оси обращения. Если работа сил, которые приводят к потерям энергии имела в сравнимые с энергией запасенной в системе, то можно считать, что механическая энергия сохраняется, а колебание являются незатухающими (это первое предположение, на котором базируются дальнейшие расчеты). На рис.1 представленные две позиции платформы.

Позиция а. Платформа проходит через положение равновесия. Механическая энергия есть чисто кинетической:

,

где: - момент инерции платформы (свободной или нагруженной), - угловая скорость в рассмотренный момент времени.

Позиция б. Платформа возвратила на угол , при этом центр масс поднялся на высоту , часть кинетической энергии перешла в потенциальную , где - масса платформы (нагруженной и свободной).

Полная механическая энергия системы определяется соотношением:

(1)

Обратимся теперь к методике определения момента инерции тела. Крайне редко экспериментатор имеет возможность провести прямые измерения необходимой величины. Обычно результат получают путем косвенных измерений. Таким образом, задачи сводится к установлению связи момента инерции с величинами, непосредственно измеренными на опыте. Очевидно, что в нашем случае это масса, время, геометрические характеристики системы: радиусы платформы - , и длины нитей - .

Установим связь между высотой и углом поворота платформы. Из рис.1 видно, что:

или (2)

Используя теорему Пифагора находим (см. рис.1а):

(3)

Теорема косинусов разрешает найти :

(4)

Подставляя выражение (3) и (4) в (2) после элементарных преобразований имеем:

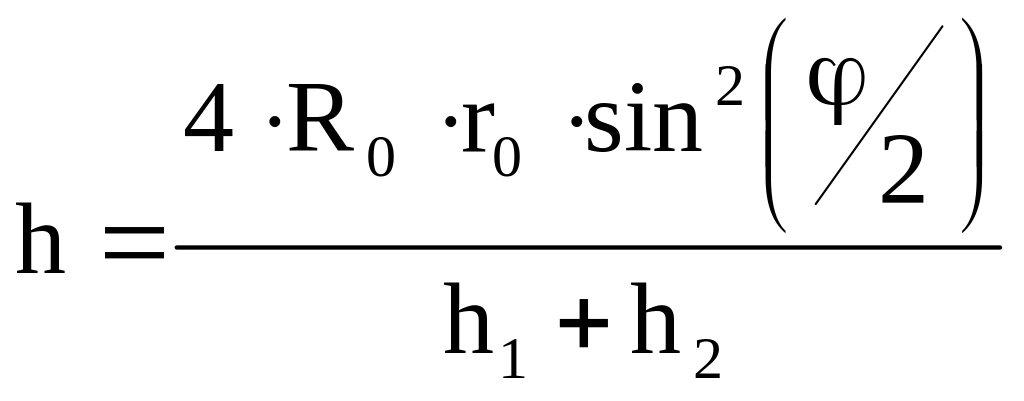(5)

Принимая во внимание неровности: имеем:

.

Таким образом, формула (5) принимает вид:

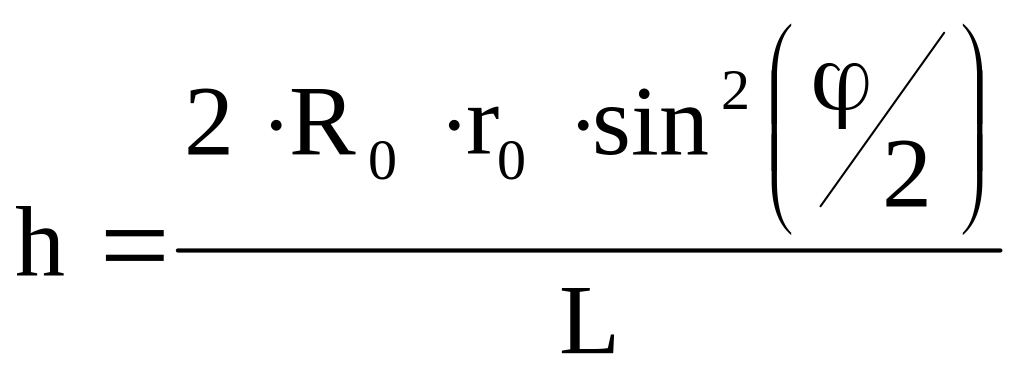(6)

Для простоты расчетов будем считать колебание малыми, т.е. (второе предположение). Несложно убедиться, что при равенство и выполняется с погрешностью в Поэтому при выполнении работы рекомендуют возбуждать колебание с амплитудой не превышающих нескольких угловых градусов. С учетом выше сказанного (6) принимает вид:

(7)

Полная механическая энергия с учетом (1) определяется соотношением:

(8)

Соответственно первому допущению , итак, производная за временем выражение (8) равняется 0, т.е.:

.

Возьмем во внимание известные кинематические соотношения:

после простых преобразований получаем:

(9)

Уравнение (9) є линейным, однородным дифференциальным уравнением второго порядка, решением которого является функция:

(10)

где: - амплитуда колебаний, - начальная фаза,  - циклическая частота колебаний. Путем подстановки (10) в (9) легко убедиться, что функция (10) тождественно удовлетворяет уравнению (9) при условии равенства:

(11)

Циклическая частота колебаний (связанная с периодом соотношением:

(12)

Учитывая (12) с (11) получаем:

(13)

Формула (13) устанавливает связь между моментом инерции платформы, периодом ее колебания, массой платформы и геометрических параметров системы. Поэтому формулу (13) следует рассматривать как рабочую.