Вычисление погрешностей измерений .

Относительная ошибка при измерении скорости пули определяется выражением:

Погрешности и малые, в сравнении с погрешностями измерений других величин и ими можно пренебречь. Тогда

;

; ;

.

Откуда ;

.

Контрольные вопросы:

1. Дайте определение момента импульса материальной точки, момента импульса твердого тела относительно оси. Объясните, почему в данной задаче можно применить закон сохранения момента импульса? Запишите этот закон относительно рассмотренной системы тел. Можно ли в данной работе использовать закон сохранения импульса?

2. На основании каких законов определяют: угловую скорость маятника, момент инерции маятника? Получите эти формулы. Следует ли проводить измерения, если пуля отскочила от мишени, не застряла в ней?

3. Выведите формулу для расчета скорости полета пули.

4. Остается ли постоянной механическая энергия системы шар-маятник в результате попадания шара в мишень? За счет работы каких сил происходит уменьшение кинетической энергии при повороте маятника. Как определить величину этой работы? К каким состояниям системы пуля-маятник применим закон сохранения механической энергии? Какие предположения при этом вводятся?

5. С какой целью в работе определяет период колебаний маятника с шаром и без него? Почему угол поворота маятника должен быть малый – не больше 5-6º? Как изменяются со временем при колебаниях маятника угловая скорость, угловое ускорение, момент импульса, момент сил упругости? Начертите графики этих зависимостей.

6. Почему необходимым условием для применения закона сохранения момента импульса есть неровность T>>τ, где Т – период колебаний маятника; τ - время торможения шара?

7. Почему при отклонении светового зайчика угол принимается равным 2α , а не α?

Литература:

Физический практикум под редакцией В.И. Ивероновой. Механика и молекулярная физика, -М., 1967.

А.Н.Матвеев. Механика и теория относительности, -М., 1976, §49, 50.

Д.В. Сивухин. Общий курс физики. т. I, Механика, -М., 1974, гл. V, §30, 32, 33, 35, 37

С.П. Стрелков. Механика, -М., 1965, гл. V, §87, гл. VII, §53, гл. XIV, §124.

С.Э. Хайкин. Физические основы механики, -М., 1975., гл. IV, §28-31, гл. XIII, §81, 89, 94, 95.

Лабораторная работа №8 Определение момента инерции махового колеса и момента силы трения в опоре

Цель работы: на основании основного закона динамики вращательного движения твердого тела и закона сохранения энергии экспериментально определить момент инерции тела правильной геометрической формы; сопоставить полученный результат с теоретическим значением.

Теоретический материал.

Вращательное движение твердого тела. Момент силы, момент инерции, Теорема Штейнера. Момент импульса твердого тела относительно оси. Уравнение движения твердого тела. Уравнение моментов. Системы материальных точек и момент сил, которые действуют на систему материальных точек.

Потенциальная и кинетическая энергии. Кинетическая энергия вращающегося твердого тела. Закон сохранения энергии. Консервативные и диссипативные системы. О законах сохранения и неконсервативных системах. Угловая скорость и ускорения. Векторы угловой скорости и ускорение. Тангенциальное ускорение.

Момент инерции является основной физической величиной, которая характеризует инертные свойства твердого тела при вращательном движении. Если распределение масс в системе известно, то вычисление момента инерции относительно выбранной оси вращения сводиться к суммированию

(1)

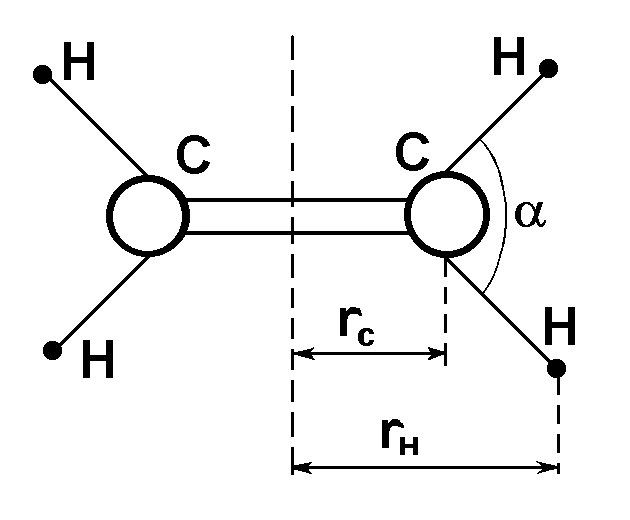
Вычислим, например, момент инерции молекулы этилена C₂H₄ относительно оси симметрии, которая проходит в плоскости черчения вертикально: для этой молекулы , и угол . Тогда , как следует из рисунка. Подставляя эти значения в (1), находим:

(гсм²).

Момент инерции молекул определяет структуру вращательного спектра молекул, по которому можно судить о межъядерных расстояниях. Для тел с непрерывным распределением плотности момент инерции может быть вычислен интегрированием

(2)

Рассчитаем момент инерции кольца, которое имеет плотность , внутренний и внешний радиусы и высоту относительно оси симметрии. Для этого мысленно выделим кольцевой элемент бесконечно малой толщины с внутренним радиусом (рис. 2). Тогда элементарный момент инерции выделенного элемента будет

.

Момент инерции всего кольца можно определить интегрированием

. (2)

Определив массу кольца и измерив штангенциркулем внешний и внутренний диаметр кольца, легко рассчитать его момент инерции. Однако в общем случае, для тел неправильной геометрической формы, момент инерции сложным образом зависит от распределения массы и вычисление интеграла (2) оказывается затруднительным. Тогда для определения момента инерции тел применяют разные экспериментальные методы.

В данной работе предлагается провести расчет момента инерции металлического кольца и определить его экспериментально, сопоставив результаты.