2. Определение средней силы соударения двух кулек.

Поскольку отведенный шарик после соударения остается в покое , то .

Тогда формулу (1) можно записать в виде

.

Где – время соударения. Откуда

(5).

Если массы шариков известны, то среднюю силу удара можно определить, зная скорость шарика в момент удара, и время соударения .

3. Определение скорости шариков при соударении.

Шарик, отведенный от положения равновесия на угол (рис. 1), имеет запас потенциальной энергии . Эта энергия сжатия переходит в кинетическую

Таким образом, , откуда

(6).

Величину h можно определить, зная угол и длину нити l. Из АВС вытекает:

, откуда .

Подставив h в уравнение (6), найдем

(7)

4. Определение времени соударения двух шариков.

Идея метода заключается в том, что шарики при ударе замыкают электрическую цепь, которая состоит из заряженного конденсатора, сопротивления и гальванометра, последовательно соединенных между собой. Для полной разрядки конденсатора через гальванометр требуется некоторое время. Если время соударения меньше, чем время полной разрядки, то при соударении конденсатор разрядится не полностью.

Зная начальный заряд конденсатора и заряд , который прошел через гальванометр за время соударения , несложно определить время соударения по формулой

(8)

Здесь C и R– емкость конденсатора и сопротивление цепи. Заряд конденсатора и заряд , прошедший за время удара , находятся с помощью баллистического гальванометра. Поскольку показывания гальванометра пропорциональны количеству электричества, которое прошло через него, то формула (8) принимает вид

(9),

где – показание гальванометра при полной разрядке конденсатора, ‑ показание гальванометра при разрядке конденсатора за время соударения шаров.

5. Время разрядки конденсатора в rc-цепи.

Рассмотрим электрическую цепь, которая состоит из заряженного конденсатора и сопротивления (рис.2). При замыкании цепи кондесатор начнет разряжаться и разность потенциалов на его обкладках будет падать. Согласно закону Ома

(10)

где – сила тока в цепи. Знак “-“ означает, что заряд конденсатора уменьшается.

Разность потенциалов на обкладках конденсатора равняется . Эти значения I и подставим в (10).

Получим

или

За время удара конденсатор изменяет заряд от до q. Интегрируя последнее дифференционное уравнение, получим . Остаточный заряд q равен начальному минус количество электричества , которое прошло через гальванометр, т.е. .

Тогда .

6. Порядок выполнения работы.

1. Подключите в электрическую цепь баллистический гальванометр и конденсатор к аккумулятору.

2. Приведите шарики в столкновение и переключите тумблер в положение “зарядка”. Через 1-2 минуты переключите тумблер в положение ”разрядка” и измерьте показания гальванометра при полной разрядке конденсатора. Опыт повторить 5 раз, данные занесите в таблицу.

3. Зафиксируйте левый электромагнит в положение, соответствующее данному углу отклонение нити. Проведите зарядку конденсатора (см. п.2), потом зафиксируйте левый шарик в гнезде электромагнита. Электромагнит включается левой кнопкой на панели установки. Переведите тумблер в положение “разрядка”. Отпустите кнопку электромагнита, при этом шарик приходит в движение. Одновременно нажмите правую кнопку, которая включает правый улавливающий электромагнит. Следите, чтобы после удара правый шарик был зафиксирован этим электромагнитом. В противном случае будет иметь место многоразовое соударение шариков и такие опыты должны выбраковываться. Измерьте показания гальванометра при разрядке конденсатора за время удара. Опыт повторите 5 раз.

4. Измените угол и повторите опыты (для 3-5 значений ).

5. Рассчитайте скорость по формуле (7), время соударения по формуле (9) и силу удара F по формуле (5). Необходимые сведения (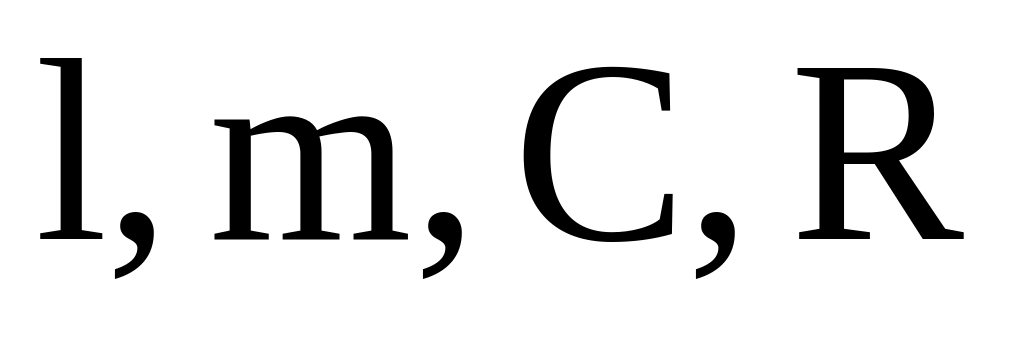 ) возьмите из таблицы. Постройте зависимость 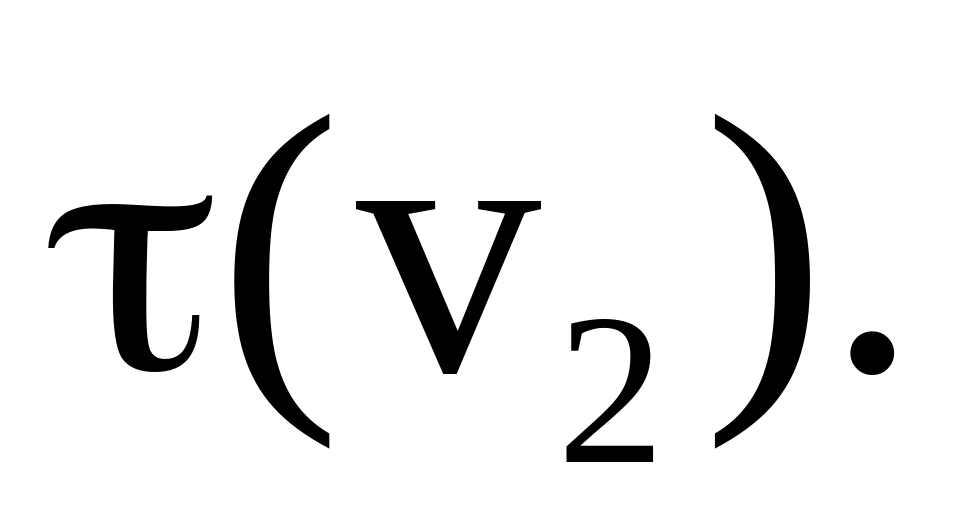Из теории удара вытекает  .

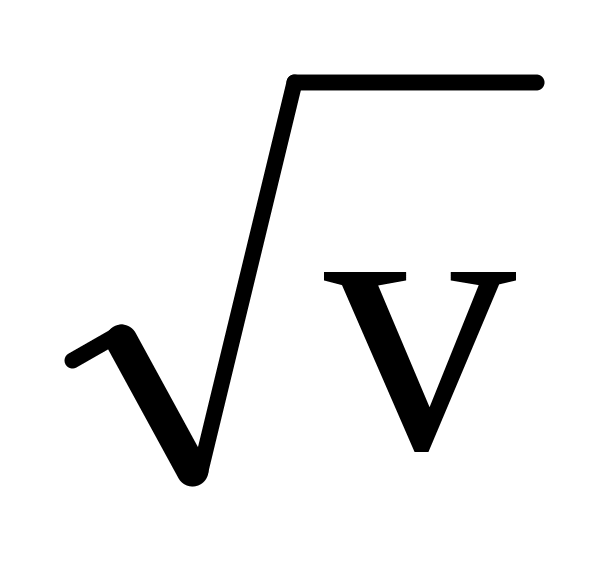Контрольные вопросы:

1. Какая система тел называется замкнутой?

2. Сформулируйте закон сохранения импульса.

3. В каких случаях для незамкнутой системы тел можно применить закон сохранения импульса?

4. Какие силы называются консервативными? Приведите примеры консервативных сил.

5. Дайте определение кинетической и потенциальной энергии.

6. Почему в поле консервативных сил можно ввести понятие потенциальной энергии?

7. Сформулируйте закон сохранения механической энергии.

8. В каком случае удар считается абсолютно упругим? Абсолютно неупругим? Какие законы механики при этом выполняется?

9. Как объяснить тот факт, что при абсолютно упругом ударе двух шаров их скорости после удара различны, а при абсолютно неупругом ударе шары двигаются после удара как одно целое?

10. Выведите формулу для расчета скорости первого шара к моменту времени, которое предшествует столкновению.

11. Как изменяются в данной задаче скорости шаров в результате столкновения?

12. В процессе столкновения шары деформируются. В какой момент времени деформация достигает своего максимального значения? Как изменились к этому моменту времени импульс и кинетическая энергия шаров в случае абсолютно упругого и абсолютно неупругого удара?

13. Каким методом в данной работе измеряется время столкновения шаров?

14. Как изменяется в процессе столкновения сила взаимодействия двух шаров в случае абсолютно упругого и неупругого удара?

Литература:

1. Физический практикум под редакцией В.И. Ивероновой, Механика и молекулярная физика, -Наука, М., 1967.

2. А.Н. Матвеев. Механика и теория относительности, -M.: Высшая школа, 1976, § 25, 27, 42, 43, 44.

3. С.Э.Хайкин, Физические основы механики, -М., гл. III, § 26, гл. IV § 28-33.

4. Д.В. Сивухин, Механика, т. I, -M.: Наука, 1974, гл. II, § 12.

5. С.П. Стрелков. Механика, -М., 1965, гл. IV.