2. Эконометрика: основные понятия и определения

Эконометрика – это наука, изучающая методами математической статистики количественные закономерности и связи в экономике, выражаемые в виде математических моделей.

Целевое назначение эконометрики – эмпирический вывод экономических закономерностей.

Основные задачи эконометрики состоят в построении моделей, выражающей выводимые закономерности, оценка их параметров и проверка гипотез о закономерностях изменения и связях экономических показателей.

Процессы эконометрического анализа могут характеризоваться двумя типами обрабатываемых данных: пространственными данными и временными рядами.

Пространственные данные – это относящиеся к одному и тому же моменту времени данные о каком-либо экономическом показателе, характеризующем однотипные объекты. Например, данные об объеме производства на разных промышленных предприятиях за один и тот же период времени или о количестве работников разных промышленных предприятий в один и тот же момент времени.

Временные ряды – это данные о каких-либо показателях, характеризующих одни и те же объекты в различные моменты времени. К такому типу данных относятся ежемесячные статистические данные за ряд лет по стране в целом или по отдельным регионам. Например, по объему промышленного производства или о количестве безработных. Особенность временных данных состоит в том, что они упорядочены во времени.

Наиболее распространены три основных класса эконометрических моделей: регрессионные модели с одним уравнением, системы одновременных уравнений и модели временных рядов.

Регрессионная модель – это уравнение, в котором объясняемая переменная представляется в виде функции от объясняющих переменных (например, модель спроса на некоторый товар в зависимости от его цены и дохода покупателей). По виду функции различают линейные и нелинейные регрессионные модели. Наиболее детально изучены и потому наиболее часто встречается в эконометрическом анализе методы оценки и анализа линейных регрессионных моделей.

Системы одновременных уравнений представляют собой системы уравнений, состоящие из регрессионных уравнений и тождеств, в каждом из которых помимо объясняющих – независимых – переменных содержатся объясняемые переменные из других уравнений системы. Пример: система, включающая уравнение спроса, уравнение предложения и тождество – уравнение равенства спроса и предложения, характеризующее рыночное равновесие.

К простейшим моделям временных рядов относятся модели тренда и модели сезонности. Тренд представляет собой устойчивое изменение уровня показателя в течение длительного времени. Сезонность характеризует устойчивые внутригодовые колебания уровня показателя. К более сложным моделям временных рядов относятся, например, модель адаптивного прогноза и авторегрессионая модель. Основная особенность моделей этого класса состоит в том, что они объясняют поведение временного ряда исходя из его предыдущих значений.

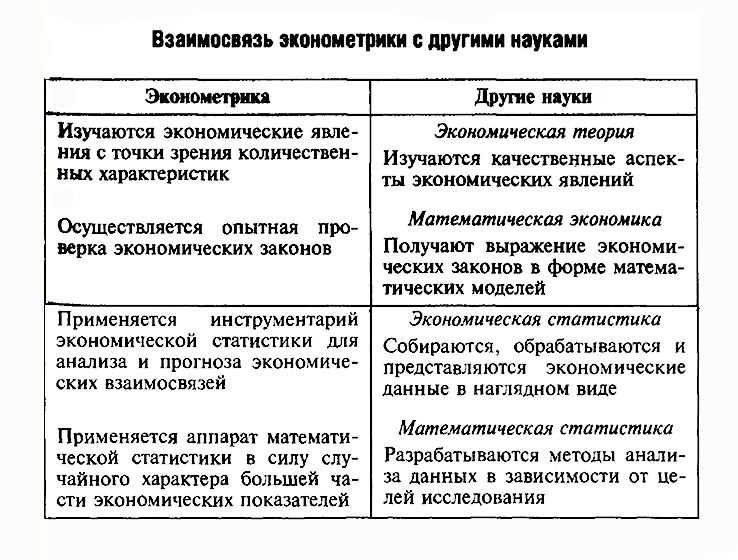
3. Предмет и задачи эконометрики

Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Один из ответов на вопрос, что такое эконометрика, может звучать так: это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или наблюдения для того, чтобы получить количественные зависимости для экономических соотношений, Данные, как правило, не являются экспериментальными, так как в экономике мы не можем проводить эксперименты.

Слово (эконометрика) представляет собой комбинацию двух слов: экономика и метрика. Таким образом, сам термин подчеркивает специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованы экономической теорией.

Можно дать такое определение эконометрики. Эконометрика- это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.

Задачей исследователя в области эконометрики является формулирование экономических моделей, основываясь на экономической теории или на эмпирических данных, оценить неизвестные величины (параметры) в этих моделях, сделать прогнозы (и оценить его точность) и дать рекомендации по экономической политике.

Во всей этой деятельности существенным является использование моделей. Модели должны быть (настолько простыми, насколько возможно, но не проще), сказал Эйнштейн. В большинстве случаев экономические законы выражаются в относительно простой математической форме.

Типы моделей

Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности и даже в исследовании политических процессов.

Математические модели полезны для более полного понимания сущности происходящих процессов, их анализа. Модель, построенная и верифицированная на основе (уже имеющихся) наблюденных значений объясняющих переменных, может быть использована для прогноза значений зависимой переменной в будущем или для других наборов значений объясняющих переменных.

Можно выделить три основных класса моделей, которые применяются для анализа и/ или прогноза.

Модели временных рядов

К этому классу относятся модели:

Тренда: у(t)=T(t)+εt,

Где Т(t )-временной тренд заданного параметрического вида (например, линейный Т(t )=а+бт, εт-случайная (стохастическая) компонента;

Сезонности: y(t)=S(t)+εt, где S(t)-периодическая (сезонная) компонента, εt-случайная (стохастическая) компонента;

Т ренда и сезонности: y(t) = T(t) + S(t) + εt (аддитивная) или

Y(t) = T(t)S(t) + εt (мультипликативная), где T(t)- временной тренд заданного параметрического вида, S(t)-периодическая (сезонная) компонента, εt- случайная (стохастическая) компонента.

К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего и др. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, на

пример, для изучения и прогнозирования объема продаж авиабилетов, спроса на мороженое, краткосрочного прогноза процентных ставок и т. п.

Регрессионные модели с одним уравнением

В таких моделях зависимая переменная У представляется в виде функции

Где х₁,х2, ,хк –независимые переменные, а B,….B_k параметры. В зависимости от вида функции f(x₁B) модели делятся на линейные и нелинейные. Например можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т. п.

Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов. Проблемам теории оценивания, верификации, отбора значимых параметров и другим посвящен огромный объем литературы. Эта тема является стержневой в эконометрике и основной в данном курсе.

Система одновременных уравнений

Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может включать в себя также объясняемые переменные из других уравнений системы. Таким образом , мы имеем набор объясняемых переменных, связанных через уравнения системы. Системы одновременных уравнений требуют относительно более сложный математический аппарат.