Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный университет путей сообщения»

Кафедра «Логистические транспортные системы и технологии»

«Логистика»

(в примерах и задачах)

Часть 2

Под ред. Н.Е. Лысенко

Рекомендовано редакционно-издательским советом

университета в качестве методических указаний

для студентов специальностей

080200 «Аналитическое обеспечение управленческих решений»,

190701 «Организация перевозок и управления на транспорте

(железнодорожный транспорт)»

Москва – - 2013

УДК 658.7

А-32

Синицына А.С., Лахметкина Н.Ю., Кузнецова И.А. Логистика (в примерах и задачах): Методические указания/ Под ред. Н.Е. Лысенко.ч.2.-М: МИИТ, 2013-55с.

Методические указания содержат задания, методику и примеры расчетов. Методические указания подготовлены по циклу практических и самостоятельных работ дисциплин «Логистика», «Основы логистики» и «Транспортная логистика».

© МИИТ, 2013

Оглавление

стр.

Введение ………………………………………………………………..……... 4

1. Прикрепление поставщиков к потребителям .………………………..… 5

2. Анализ деятельности строительной компании (фирмы)……………..… 8

3. Управление качеством строительной продукции……………………… 26

4. Принципиальная модель экономических потоков

строительной фирмы ……………………………………………………...…. 35

Приложение 1 ……………………………………………………………..…. 42

Приложение 2 ………………………………………………………………… 44

Приложение 3 ……………………………………………………….……..… 50

Приложение 4 ……………………………………………………….……..… 53

Список использованной литературы ……..………………………………… 54

Введение

В методических указаниях рассматриваются методика и примеры решения практических задач, относящихся к сфере логистики строительства.

Данная разработка является второй частью указаний, посвященных данной проблеме. В них включены методики и примеры решения задач наиболее часто встречающихся в практической деятельности специалистов в области строительства. В их числе: прикрепление поставщиков к потребителям, анализ деятельности строительной компании (фирмы), управление качеством продукции, построение принципиальной модели экономических потоков строительной фирмы.

К каждой задаче в конце указаний даются приложения, содержащие условные исходные данные (стоимостные и временные показатели). Номера вариантов исходных данных рекомендуемых для использования в расчетах задаются преподавателем, ведущим практические занятия.

Перечень приводимых работ далеко не исчерпывает их возможные варианты. В связи с этим, авторы будут весьма благодарны всем пользователям методических указаний за их пожелания.

1. Прикрепление поставщиков к потребителям

Задача. Однородный груз сосредоточен у 3 поставщиков соответственно в объемах 120, 148 и 148 т. Данный груз необходимо доставить 4 потребителям в объемах 129, 122, 104 и 61 т. Известны стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. В таблице 1.1 К1-К4 – потребители, П1-П3 – поставщики. Требуется составить такой план перевозок, при котором запасы всех потребителей полностью удовлетворены и суммарные затраты на перевозку всех грузов минимальны. Исходные данные приведены в Приложении 1.

Таблица 1.1

	К1	К2	К3	К4	Предложение
П1	45	24	21	30	120
П2	24	78	28	18	148
П3	60	20	55	13	148
Спрос	129	122	104	61	416

Методика решения. Исходные данные транспортной задачи обычно записываются в виде таблицы (табл. 1.2).

Таблица 1.2

			…
			…
…	…	…	….	….
			…

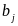
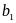
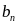
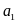
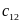
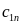
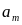
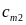
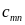
Переменными (неизвестными) транспортной задачи являются i=1,2,…m; j=1,2,…n – объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные можно записать в виде матрицы перевозок

(1.1).

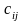
Так как произведение определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны . По условию задачи требуется обеспечить минимум суммарных затрат. Следовательно, целевая функция имеет вид

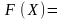
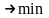(1.2)

Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:

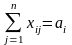, i=1,2,…,m (1.3)

Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:

, j=1, 2, … , n (1.4)

Учитывая условие положительности объемов перевозок,

, i=1,2,,…,m, j=1,2,…,n (1.5)

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.

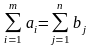. (1.6)

Формулировка транспортной задачи такова: найти переменные задачи , i=1,2,…m; j=1,2,…n, удовлетворяющие системе ограничений (1.3), (1.4), условиям положительности (1.5) и обеспечивающие минимум целевой функции (1.2). Исходные данные для расчетов принимаются по приложению 1. Решение задачи возможно путем использования средств Excel – «поиск решения» или при помощи математических методов – примеры приведены в табл. 1.3, 1.4 (например, методом северо-западного угла – табл. 1.3).

Таблица 1.3

	К1	К2	К3	К4	Предложение
П1	120	-	-	-	120
П2	9	122	17	-	148
П3	-	-	87	61	148
Спрос	129	122	104	61	416

Суммарные затраты на перевозку всех грузов при данном распределении составят: С=45*120+24*9+122*78+28*17+55*87+61*13=21186

Таблица 1.4

	К1	К2	К3	К4	Предложение
П1	-	16	104	-	120
П2	129	19	-	-	148
П3	-	87	-	61	148
Спрос	129	122	104	61	416

Суммарные затраты на перевозку всех грузов при данном распределении составят: С=129*24+24*16+19*78+87*20+10*21+61*13=9679

Так как по условию задачи (формула (1.2)) требуется обеспечить минимум суммарных затрат на перевозку всех грузов, оптимальным распределением является вариант представленный в табл. 1.4.