3 Синтез параметрів розрахункових статичної характеристик звт методом найменших модулів

При рішенні задачі методом найменших модулів значення параметрів q1,q2,…qn розрахункової статичної характеристики ЗВТ намагаються підібрати так, щоб графік цієї характеристики був заключений між двома кривими, які віддалені від графіка заданої статичної характеристики ЗВТ у= fз(х) на однакову величину, рівну максимальній похибці наближення Δmax.

У цьому випадку у = fр(х; q1, q 2,… qn) має властивості кривої найменших модулів (КНМ), тобто такої кривої, максимальне відхилення якої від у = fз(х) на інтервалі Хn ≤ Х ≤Хv є мінімальним.

Параметри q1, q 2,… qn задовольняють критеріям мінімакса:

Мах mod (q1, q 2,… qn) = max | fр (х; q1, q 2,… qn) – fз (х) | = min

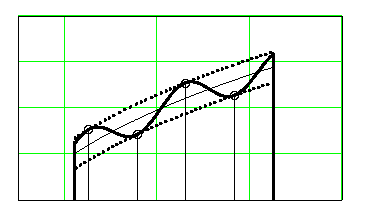
Розрахунок кривої найменших модулів (КНМ) і максимальної зведеної похибки наближення (МЗП) аналогічний розрахунку прямої найменших модулів (ПНМ) і максимальної зведеної похибки від нелінійності статичної харакетристики ЗВТ.

Послідовність рішення цих задач тотожня.

4 Синтез параметрів розрахункових статичних характеристик методом найменших квадратів

При рішенні задачі методом найменших квадратів вибір параметрів q1,q2,…qn розрахункової статичної характеристики ЗВТ відповідає умовам мінімума функції, яка виражає математичне очікування квадрата похибки наближення.

Крива у = fр(х; q1, q 2,… qn) з параметрами q1, q 2,… qn, що задовольняють цим умовам, називається кривою найменших квадратів (КНК).

Ступінь близькості КНК до бажаної статичної характеристики ЗВТ оцінюється за величиною середньоквадратичної зведеної похибки наближення (СЗП):

δn = √Dn min / │ fзv - fзn │,

де Dn min – мінімальне значення функції;

fзn, fзv – граничні ординати бажаної характеристики ЗВТ.

Тому, у загальному випадку, розрахунок КНК та СЗП зводиться до пошуку умовного екстремума (мінімума) неявно заданої функції змінних q1, q 2,… qn.

Відомо, що ця задача тотожня пошуку звичайного екстремума функції Лагранжа.

Тема корекція статичної характеристики звт

План

1 Застосування коригуючих ланок і спеціальних обчислювачів

2 Кусочно-лінійна апроксимація статичної характеристики ЗВТ

3 Сплайн-апроксимація статичної характеристики ЗВТ

1 Застосування коригуючих ланок і спеціальних обчислювачів

Однією з основних задач, яку доводиться вирішувати при проектуванні нового ЗВТ, є задача забезпечення заданих метрологічних характеристик (особливо, похибки ЗВТ).

Похибка наближення може перевищувати допустиму похибку. В цьому випадку, для досягнення заданої точності вимірювань рекомендується:

1. використовувати включення у схему ЗВТ додаткової корегуючої ланки, яка

змінює загальну статичну характеристику приладу;

2. використовувати спеціальний обчислювач результату вимірювань.

У першому випадку функцію перетворення, параметри та місце підключення корегуючої ланки добирають так, щоб загальна статична характеристика коригоючого пристрою співпадала з бажаною характеристикою ЗВТ, або була дуже близькою до неї.

У другому випадку прилад може мати спеціалізований обчислювач, в якому реалізують алгоритм, що дозволяє за значенням вихідного сигналу аналогової частини приладу обчислити результат вимірювань.