
- •Тема 1 системний підхід до проектування вимірювальних систем
- •1 Значення проектування засобів вимірювальної техніки
- •2 Етапи створення математичної моделі звт
- •3 Структурна схема звт
- •Тема 2 задачі аналізу статичної характеристики звт
- •1 Поняття про статичний режим вимірювань
- •2 Види статичних характеристик звт
- •Рішення
- •Тема 3 аналіз і розрахунок похибки від нелінійності статичної характеристики засобів вимірювальної техніки
- •1 Нелінійність статичних характеристик і її джерела
- •2 Розрахунок максимальної зведеної похибки від нелінійності статичної характеристики засобів вимірювальної техніки
- •3 Розрахунок середньоквадратичної зведеної похибки від нелінійності статичної характеристики звт
- •Відповідне значення дорівнює:
- •4 Властивості зведеної похибки від нелінійності статичної характеристики звт
- •Тема 4 методи синтезу розрахункової статичної характеристики
- •1 Проектування звт як аналіз, синтез і оптимізація
- •2 Синтез параметрів розрахункових статичних характеристик звт методом інтерполяції
- •3 Синтез параметрів розрахункових статичної характеристик звт методом найменших модулів
- •Тема корекція статичної характеристики звт
- •1 Застосування коригуючих ланок і спеціальних обчислювачів
- •2 Кусочно-лінійна апроксимація статичної характеристики звт
- •3 Сплайн-апроксимація статичної характеристики звт
- •Тема методи розрахунку градуювальної статичної характеристики звт
- •1 Розрахунок градуювальної статичної характеристики звт
- •2 Розрахунок градуювальної характеристики звт методом середніх
- •3 Розрахунок градуювальної характеристики звт методом найменших квадратів
- •4 Розрахунок градуювальної характеристики методом Асковиця
- •5 Розрахунок градуювальної характеристики звт методом найменших модулів
- •1 Динамічні метрологічні характеристики
- •2 Розрахунок передатної функції за структурною схемою звт
3 Розрахунок середньоквадратичної зведеної похибки від нелінійності статичної характеристики звт
Прямою найменших квадратів (ПНК) називається пряма уа = А+Вх, середньоквадратичне відхилення якої від кривої у=f(х) на інтервалі
Хn ≤ Х ≤ Хν є мінімальним.
Параметри А і В такої прямої визначаються з умови мінімума математичного очікування квадрата похибки наближення:
![]() ,
,
де
![]() - ФГРВ вимірюваної
фізичної величини Х;
- ФГРВ вимірюваної
фізичної величини Х;
![]() – середнє значення
квадрата відхилення кривої f(х) від
прямої уа
– середнє значення
квадрата відхилення кривої f(х) від
прямої уа
(тобто математичне очікування квадрата похибки наближення р(х;А;В)).
За відсутністю відомостей про характер розподілення значень вимірювальної величини х закон її розподілення приймають равномірним, тобто вважають,що:
![]() ,
якщо
,
якщо
![]() ,
,
![]() ,
якщо
,
якщо
![]() .
.
Параметри А і В ПНК розраховуються за формулами:
А=
 В
=
В
=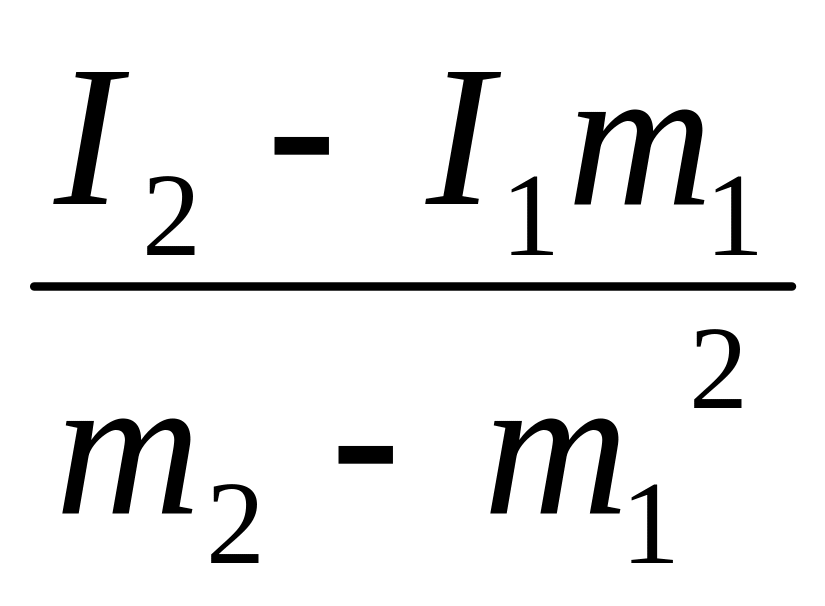
де
![]() –
визначені інтеграли, які залежать від
форми ФГРВ рх(х)
і форми статичної характеристики ЗВТ
f(х).
–
визначені інтеграли, які залежать від
форми ФГРВ рх(х)
і форми статичної характеристики ЗВТ
f(х).
Тобто, задача розрахунку ПНК зводиться до розрахунків чотирьох визначених інтегралів:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Мінімальне значення функції D(А,В) дорівнює:
![]() ,
,
де
![]() .
.
Рівняння ПНК обирають за тими же правилами, що і рівняння ПНМ.
Якщо уа =А + Вх, то розрахунок параметрів А і В ПНК виконують за наведеними вище формулами.
Якщо уа = Вх і Хn =0, то коефіцієнт наклону В розраховують за формулою:
![]() .
.
Відповідне значення дорівнює:
![]() .
.
Ступінь близькості ПНК до графіку статичної характеристики ЗВТ оцінюється величиною середньоквадратичної зведеної похибки від нелінійності яка розраховується за формулою:
![]() ,
,
4 Властивості зведеної похибки від нелінійності статичної характеристики звт
Якщо F(х) = в∙ f(х), (в≠0), то РF (Хn; Хν ) = Рf (Хn; Хν),
тобто множення статичної характеристики ЗВТ f(х) на постійний коефіцієнт в≠0 не впливає на значення зведеної похибки від нелінійності цієї характеристики.
Якщо F(х) = а + f(х), то РF (Хn; Хν) = Рf (Хn; Хν),
тобто зміщення графіка статичної характеристики ЗВТ f(х) уздовж осі ординат не впливає на значення зведеної похибки від нелінійності цієї характеристики.
Якщо F(х) = а + в· f (х), то РF (Хn; Хν) = Рf (Хn; Хν),
тобто лінійне перетворення статичної характеристики ЗВТ f(х), приводить до нової характеристики F(х), яка має теж саме значення зведеної похибки від нелінійності (витікає з 1 і 2).
Якщо F(х) = f(в·х), (в≠0), то РF (Хn; Хν) = Рf( в· Хn; в· Хν ).
тобто змінення масштабу вхідного сигналу не змінює значення зведеної похибки від нелінійності цієї характеристики.
Якщо F(х) = f(х-а), то РF (Хn; Хν) = Рf (Хn-а; Хν-а)
тобто зміщення графіка статичної характеристики ЗВТ f(х) уздовж осі абсцис не змінює значення зведеної похибки від нелінійності цієї характеристики.
Якщо F(х) = f(а + в∙х), то РF (Хn; Хν) = Рf (а + в∙Хn; а + вХν),
тобто лінійне перетворення аргумента функції fх не змінює значення зведеної похибки від нелінійності статичної характеристики ЗВТ
(витікає з 4 і 5).
7) Рf (Хn; Хν) = Рψ (уn; уv),
тобто зведені похибки від нелінійності прямої і зворотної статичних характеристик ЗВТ дорівнюють.
Об’єднавши всі властивості, можна сказати, що два ЗВТ мають однакове значення зведеної похибки від нелінійності, якщо статичні характеристики цих ЗВТ мають однакову форму.
