Векторний добуток векторів

Трійка векторів , , називається правою, якщо з кінця вектора поворот від вектора до вектора видно проти годинникової стрілки. У протилежному випадку трійка векторів називається лівою.

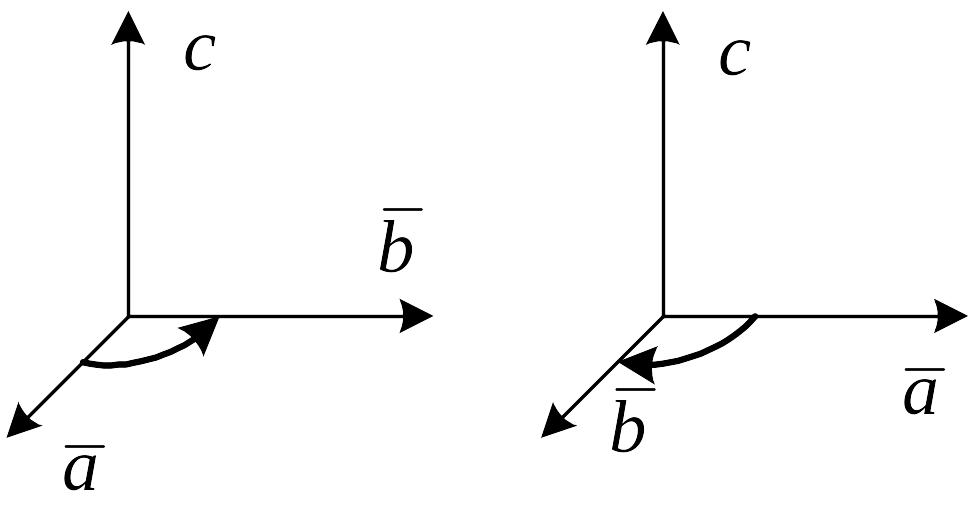
а) б)

Рис.15

Афінна чи декартова система координат (рис.15 а) б)) називається правою (лівою), якщо три базисних вектора утворюють праву (ліву) трійку. Надалі будемо користуватися правими системами координат.

Векторним добутком векторів і називається такий третій вектор , для якого виконуються наступні умови:

1. вектор перпендикулярний до кожного з векторів і (а отже і до площини векторів і );

2. вектори , , утворюють праву трійку;

3. , де - кут між векторами і .

Векторний добуток звичайно позначають: або .

Геометричні властивості.

1º. Необхідною і достатньою умовою колінеарності двох векторів є рівність нулю їх векторного добутку.

Для доведення досить відмітити, що кут між колінеарними векторами дорівнює або нулю, або 180°.

2º. Якщо вектори і зведено до спільного початку, то , де - площа паралелограма, побудованого на векторах і (рис.16).

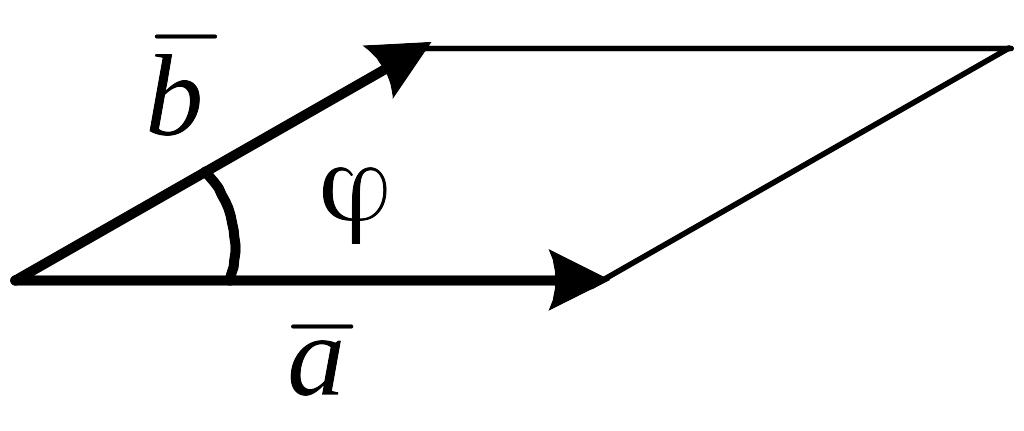
Рис.16

Звідси ,

де – одиничний вектор, який задовольняє умовам: , , вектори , , утворюють праву трійку.

Алгебраїчні властивості.

Для будь-яких векторів , , і будь-якого числа мають місце такі співвідношення:

3º. = – антикомутативність;

4º. , – асоціативність;

5º. , – дистрибутивність відносно додавання векторів.

Доведемо властивість 3°. Для цього досить відмітити, що = ; вектори, які записано в лівій і правій частинах рівності яка доводиться, є колінеарними, бо вони обидва перпендикулярні до площини векторів і ; при цьому вектори , , утворюють праву трійку, а вектори , , – ліву; отже трійка , , є також правою. Властивість 3° цим доведено.

Задача10. Обчислити площу паралелограма, побудованого на векторах і , де , , .

Розв’язання.

За означенням векторного добутку . Знайдемо

Отже,

Задача 11. Для кожної з можливих пар базисних векторів , , обчислити векторний добуток їх компонентів.

Розв’язання.

Врахуємо, що базисні вектори взаємно перпендикулярні, мають одиничну довжину і трійка , , є правою; тоді одержимо:

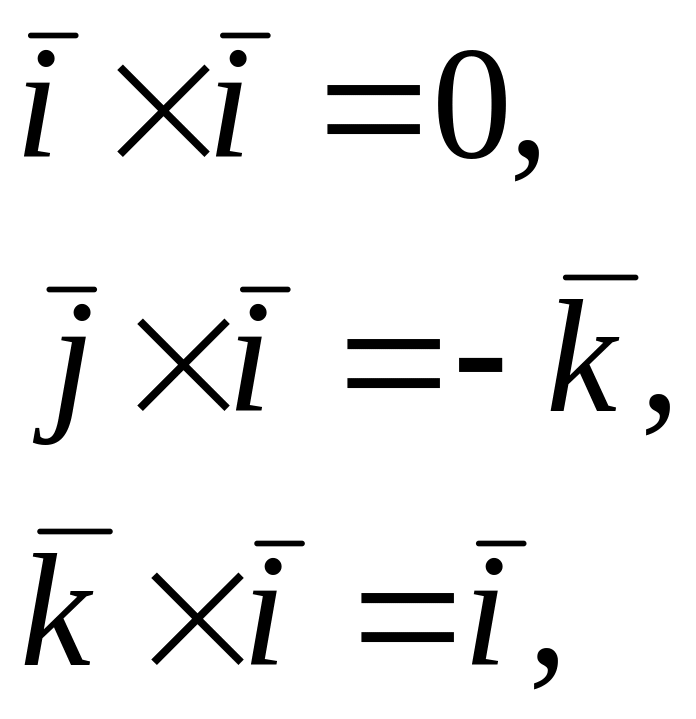
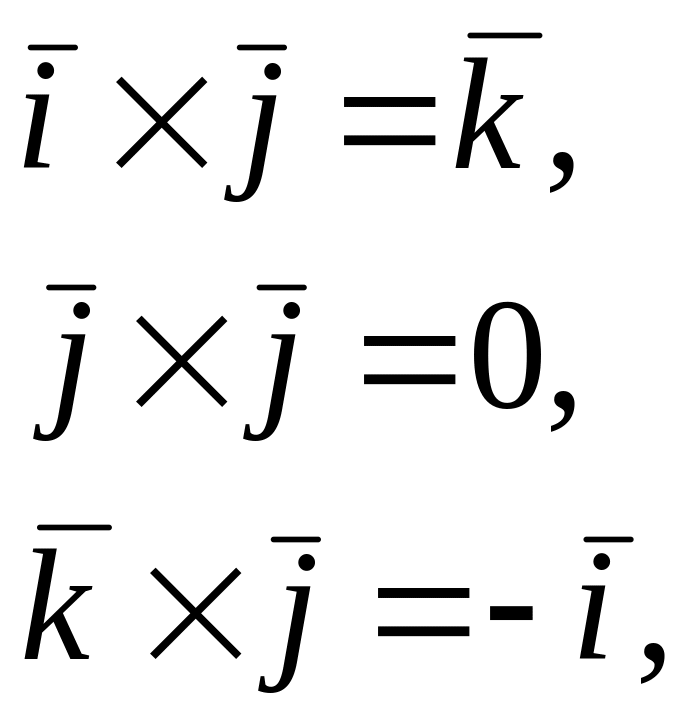
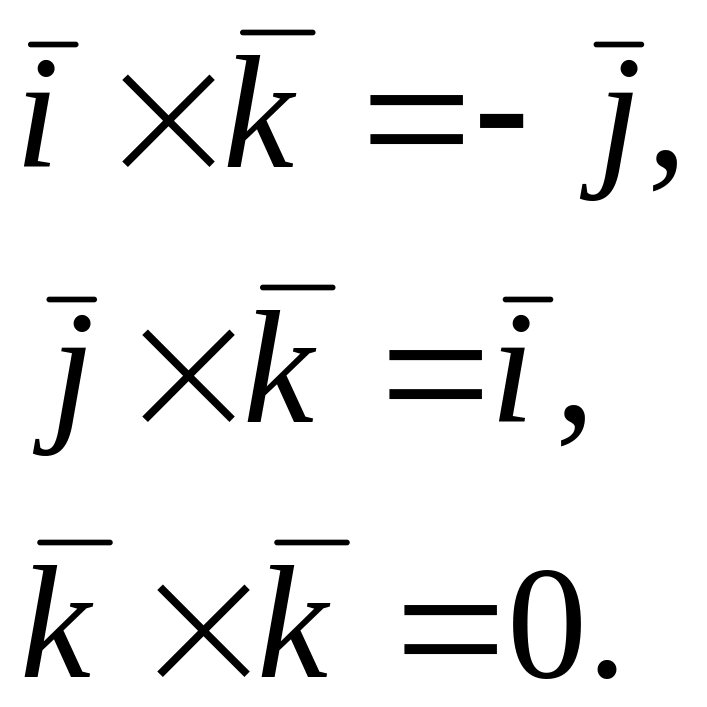
Запис векторного добутку через координати векторів.

Визначником другого порядку називається число, яке обчислюється за наступним правилом:

Визначником третього порядку називається число, яке можна обчислити за наступним правилом:

Теорема 5. Якщо два вектора і визначені своїми декартовими прямокутними координатами , , в базисі , , , то векторний добуток цих векторів має вигляд:

(5)

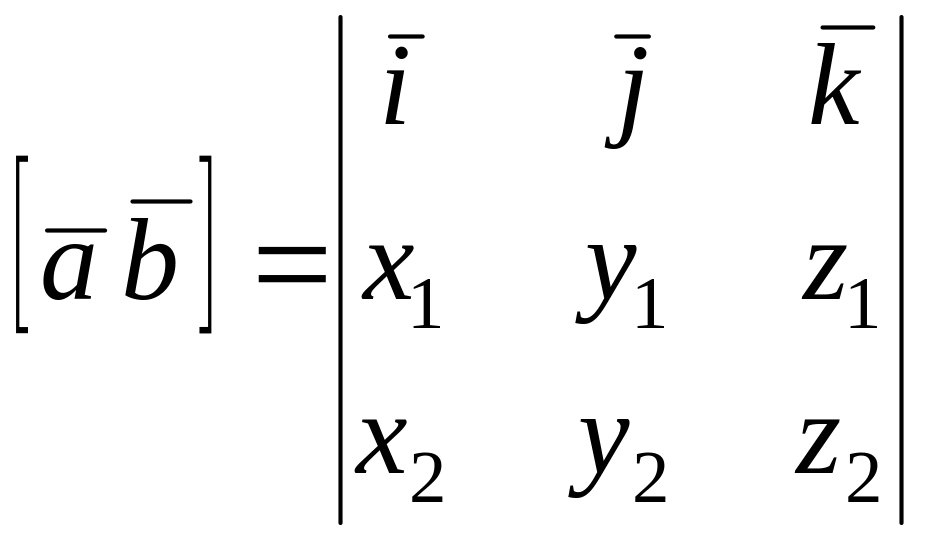або . (6)

Доведення:

Зауважимо перш за все, що з останнього запису векторного добутку легко отримати попередній: для цього досить обчислити визначник, розклавши його за елементами першого рядка.

Виразимо вектори і через орти , , :

; .

Перемножимо одержані вирази векторно, для чого скористаємось алгебраїчними властивостями векторного добутку і задачею 17.

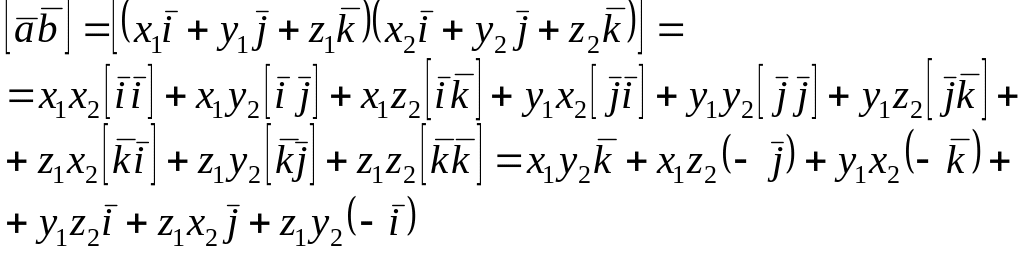
отже,

Одержана рівність еквівалентна (5). Теорему доведено.

Задача 12. Обчислити векторний добуток векторів і .

Розв’язання:

Задача 13. Знайти площу паралелограма, побудованого на векторах і .

Розв’язання.

З означення векторного добутку випливає, що площу паралелограма, побудованого на векторах і , можна обчислити за формулою: причому вектори і розглядались в просторі. Нам потрібно одержати формулу для обчислення площі паралелограма, побудованого на векторах, що лежать на площині. Для цього приймемо, що площина векторів і співпадає з координатною площиною в тривимірному просторі, а вісь Оz перпендикулярна до цієї площини. Тоді вектори і можна записати як тривимірні, з рівними нулю третіми координатами:

, .

Знайдемо векторний добуток

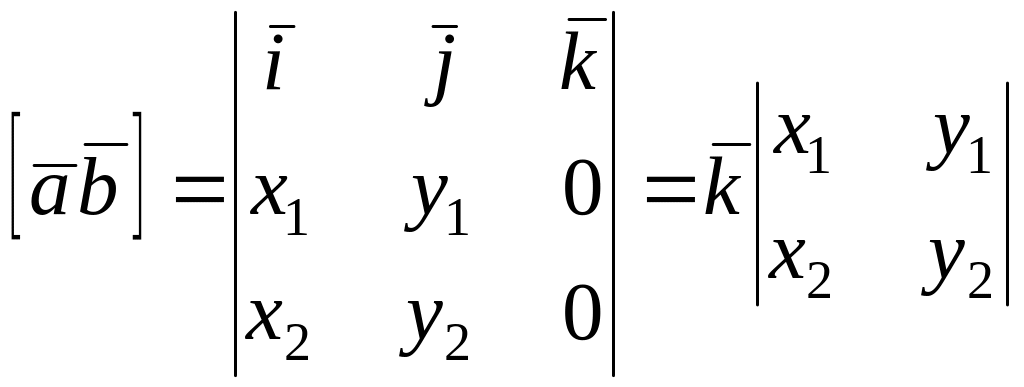
і його модуль:

,

отже,

.

Зауваження. Площа трикутника побудованого на векторах і обчислюється за формулою:

.

Задача 14. Обчислити площу трикутника, вершинами якого є точки А(4;2), В(9;4); С(7;6).

Розв’язання. Знайдемо координати векторів , . Тоді

(кв.од).