Тема 2. Система координат. Ділення відрізка в даному відношенні.

У

Рис.8

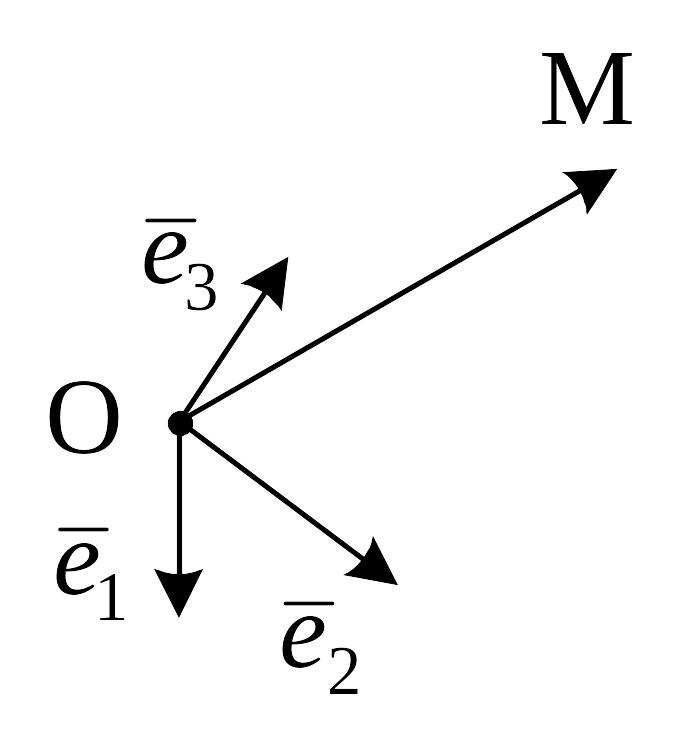
просторі зафіксуємо точку О і виберемо базис , , . Тоді кожній точці М простору можна однозначно поставити вектор , а значить і впорядковану трійку чисел – координат цього вектора (рис.8).

Афінною системою координат називається сукупність точки О і базису , . Координати радіуса-вектора точки М називаються афінними координатами точки М у даній системі координат.

Афінні координати точки М позначають, наприклад, так: М(x; y; z).

Задача 1. Дві точки в деякій афінній системі координат (О, , ) задано координатами А(x₁, y₁, z₁), В(x₂, y₂, z₂) (рис.9). Знайти координати вектора .

Розв’язання.

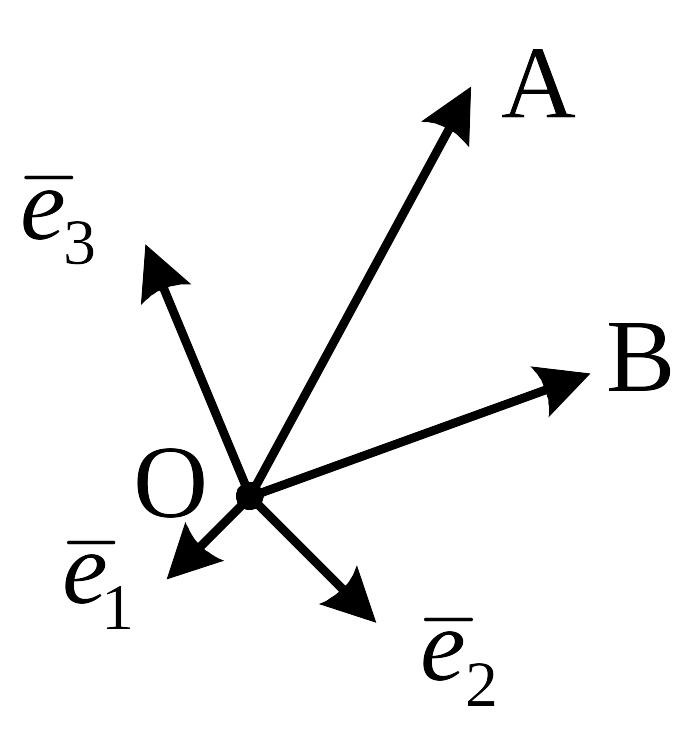
Рис.9

За правилом трикутника , звідки .

З означення афінних координат точки маємо, що (x₂, y₂, z₂), (x₁, y₁, z₁). Тоді, виходячи з теореми 3 про дії над координатами, одержуємо: (x₂–х₁, y₂–y₁, z₂–z₁).

Висновок. Щоб знайти координати вектора, треба від координат його кінця відняти відповідні координати початку.

Задача 2. Розкласти вектор = + + за базисом, визначеним векторами = + –2 , = – і =2 +3 .

Розв’язання.

Розкласти вектор за базисом , , – це значить подати його у вигляді ,

де , , - невідомі числа

Маємо:

= + + = ( + –2 )+ ( – )+ (2 +3 ).

Використовуючи властивості лінійних операцій над векторами, одержуємо:

+ + =( + ) +( – +2 ) +(–2 +3 ) .

Внаслідок того, що розкладання вектора за базисом може бути єдиним, прирівнюємо коефіцієнти при відповідних векторах:

Розв’язуючи одержану систему лінійних рівнянь, маємо:

, , .

Отже, шуканим розкладанням є:

.

Ділення відрізка в даному відношенні.

Нехай відносно базису , , дві фіксовані точки А і В мають координати: А(X_А, Y_А, Z_А), В(X_В, Y_В, Z_В). Знайдемо координати x, y, z точки М, яка належить прямій АВ і ділить відрізок АВ в деякому відношенні 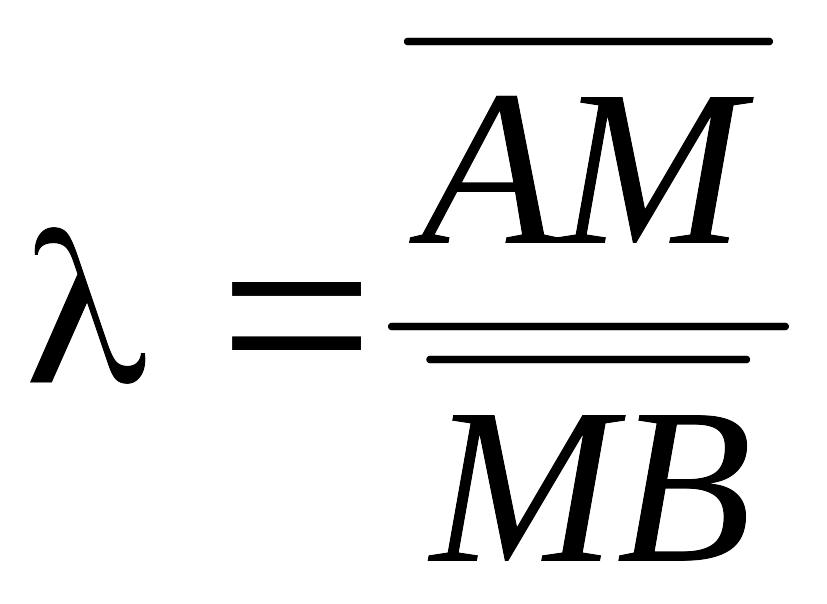(рис.10). Зауважимо, що коли точка М знаходиться між точками А і В, то ↑↑ і ; при цьому кажуть, що точка М ділить відрізок АВ внутрішнім способом. Якщо точка М' лежить на прямій АВ зовні відрізка АВ, то ↑↓ і ; при цьому кажуть, що точка М' ділить відрізок АВ зовнішнім способом.

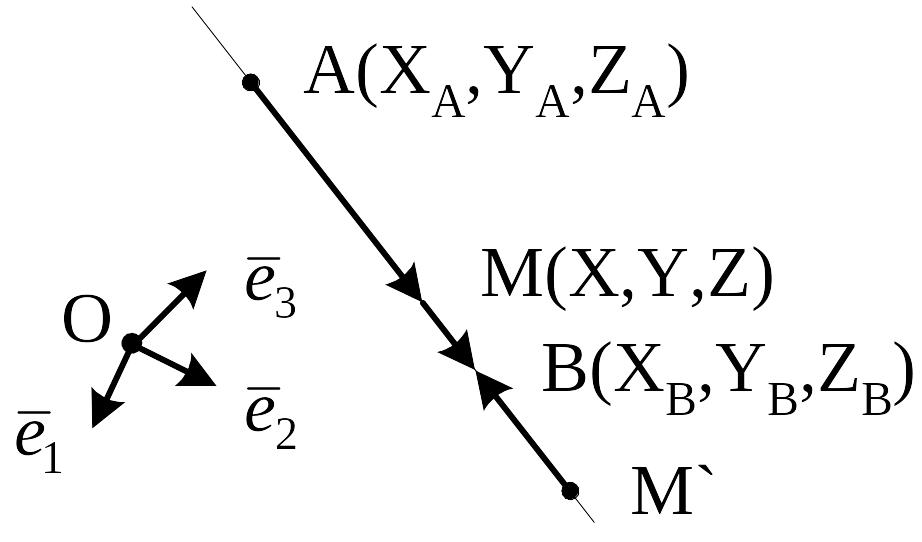
Рис.10

Наше завдання полягає в тому, щоб, знаючи координати точок А, В і величину , знайти координати точки М.

Враховуючи залежність

,

знаходимо координати векторів

(X–X_А; Y–Y_А; Z–Z_А), (X_В–X; Y_В–Y ; Z_В–Z) і, користуючись теоремою єдиного розкладання вектора за базисом, маємо:

Звідси (1)

Формули (1) і є формули ділення відрізка АВ в даному відношенні, де

Наслідок. Якщо точка М є серединою відрізка АВ, то і одержані формули мають вигляд:

; ; . (2)

(2) це є формули ділення відрізка АВ навпіл.

Координати середини відрізка дорівнюють півсумі відповідних координат його кінців.

Зауваження. Якщо відрізок розташований в якій-небудь координатній площині, наприклад, О_xy, то для всіх його точок z=0 і для визначення координат точки М досить скористатися першими двома формулами з (1) чи (2).