Опорні конспекти з теми „Векторна алгебра” з історії векторів.
Термін “вектор” походить від латинського слова vector, що означає – “той, що несе”.
Уперше, в 1587 році, фламандський учений Сімон Стевін, розглядаючи додавання сил, прийшов до висновку, що для знаходження результату необхідно скористатися “паралелограмом” сил, при цьому для позначення сил він скористався стрілками.
Довгий час вектор розглядався тільки як напрямлений відрізок, який визначається своїм початком і кінцем. З розробкою теорії геометричних перетворень вектор почали розглядати не тільки як напрямлений відрізок, але і як паралельне перенесення.
Початки векторного числення були вперше викладені Фрідріхом Вільгельмом Бесселем — німецьким астрономом, математиком і геодезистом, який був членом Берлінської АН. Ось його означення суми кількох напрямлених відрізків: “Щоб скласти більше, ніж два відрізка, необхідно слідувати правилу: розміщуємо їх так, щоб кінець першого співпадав з початком другого, а кінець другого співпадав з першою точкою третього і так далі, потім з тією точкою, де останній відрізок закінчився, і називається цей останній відрізок сумою всіх даних відрізків”.
Французький
учений Карно вводить позначення вектора
за допомогою риски зверху: 
,
.
Німецький математик Август Фердинанд
Мебіус вперше подав геометричну кількість
AB
у вигляді різниці координат точок B
і A.
Однак, вважається, що основоположниками
векторної алгебри є англійський
математик У. Гамільтон (1805 – 1865) і
німецький математик Г. Грассман (1809 –
1877). Гамільтон першим став застосовувати
термін “вектор”
і оперувати з ним у тривимірному просторі.
Він вперше ввів терміни “скаляр”,
“скалярний
добуток”.
Грассман уперше виклав учення про 
вимірний
векторний простір.
Вектори
він називав палочками і позначав їх
жирними літерами латинського алфавіту.
Скалярний добуток, який називають ще
внутрішнім, він позначив 
,
а векторний, який називають зовнішнім,
–
.
Елементи векторної алгебри Тема 1. Означення вектора.
Вектором називається напрямлений відрізок (або впорядкована пара точок).
П
означення:
,
(рис.1)
Нульовий
вектор – це вектор, початок якого
співпадає з його кінцем. Наприклад,
.
Відстань
між початком і кінцем вектора називається
довжиною
(модулем
або абсолютною
величиною)
вектора:
,
.
Якщо довжина вектора дорівнює одиниці,
то він називається одиничним або ортом
(orientation,
лат. - орієнтація). Позначення орта
вектора
:
.
Вектори,
розташовані на одній або на паралельних
прямих називаються колінеарними
(позначення:
||
).
Н
априклад
(рис.2):
||
;
||
;
||
;
↑↑ – однаково напрямлені (співнапрямлені) вектори
↑↓ ; ↑↓ – протилежно напрямлені вектори.
Вважається, що напрям нульового вектора невизначений і цей напрям є колінеарним будь-якому вектору.
Вектори, які розташовані на прямих, паралельних одній площині, називаються компланарними.
Рівними називаються вектори, які колінеарні, однаково напрямлені і мають рівні модулі:
З цього означення випливає, що вектори не змінюються при паралельному перенесенні. Отже, ми розглядаємо так звані вільні вектори.
Добутком
вектора
на
дійсне число
називається вектор
,
який задовольняє наступним умовам:
Наприклад
(рис.3),
;
;
.
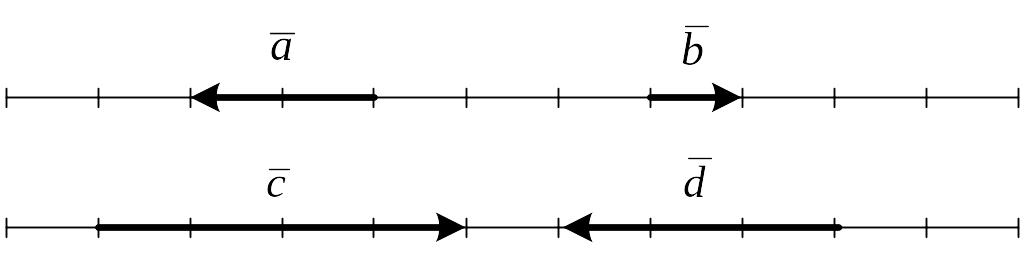
Рис.3
Сумою + двох векторів і називається вектор, який сполучає початок вектора з кінцем вектора за умови, що вектор відкладено від кінця вектора .
Рис.4
Це означення дозволяє побудувати суму будь-яких двох векторів і називається правилом трикутника (рис.4). Причому, очевидно, що сума двох векторів не залежить від вибору початкової точки А. Таким чином, для будь-яких трьох точок А, В і С має місце рівність:
.
Другий спосіб побудови суми двох векторів – так зване правило паралелограма (рис.5):
Якщо
вектори
і
відкласти від спільного початку О, то
сумою
+
є вектор
,
який виходить з тієї ж точки О і співпадає
з діагоналлю паралелограма, яка виходить
з точки О.
Очевидно, що це правило є наслідком правила трикутника. Ним можна користуватися, якщо вектори-доданки не колінеарні.