2. Застосування методу Гаусса для обчислення оберненої матриці.

Метод Гаусса є універсальним у разі розв’язуванні систем лінійних рівнянь. Цей метод можна застосувати для обчислення оберненої матриці, що набагато простіше за спосіб, розглянутий у п.1.4.

Аби знайти обернену матрицю, потрібно виконати такі дії:

1. До даної матриці А справа дописати одиничну матрицю Е;

2. Елементарними перетвореннями над рядками матриці (А|E) матрицю А звести до одиничної матриці.

У результаті на місці даної матриці А буде сформовано одиничну матрицю, а на місці дописаної справа одиничної матриці Е знаходитиметься обернена матриця А^-1, тобто замість матриці (A|E) дістанемо матрицю (E|A^-1).

П р и к л а д 1.19. знайдемо матрицю, обернену до матриці

До даної матриці А справа допишемо одиничну матрицю Е. За допомогою елементарних перетворень над рядками матриці (A|E) матриця А зводиться до одиничної матриці:

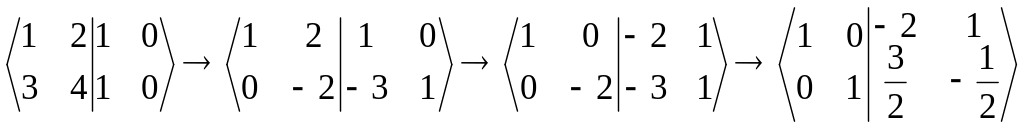
Отже, обернена матриця

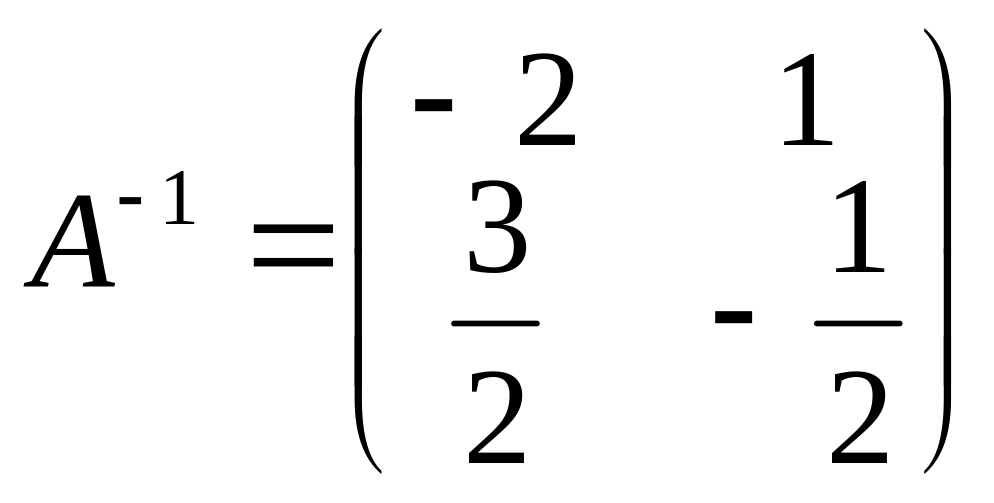
Правильність виконання обчислень легко безпосередньо перевірити за означенням АА^-1 = А^-1А = Е

0. Економічні задачі, що зводяться до систем лінійних рівнянь

Приклад.

Для випуску виробів трьох видів (α,β,γ) підприємство використовує сировину 3-х типів (S_1, S_2, S₃). Норми витрат кожного з типів сировини на один виріб і обсяг витрат сировини за один день задано таблицею:

Вид сировини	Норми витрат на один виріб, ум. од.			Витрати сировини за 1 день, ум. од.
	α	β	γ
S1	9	3	4	2700
S2	7	1	6	2700
S3	14	5	6	4200

Знайти щоденний обсяг випуску кожного виду виробів

Розв’язування.

Припустимо, підприємство щодня виробляє х₁ одиниць виробів виду α, х₂ одиниць – β і х₃ одиниць виробів виду γ. Тоді відповідно з витратами сировини кожного виду, маємо систему

;

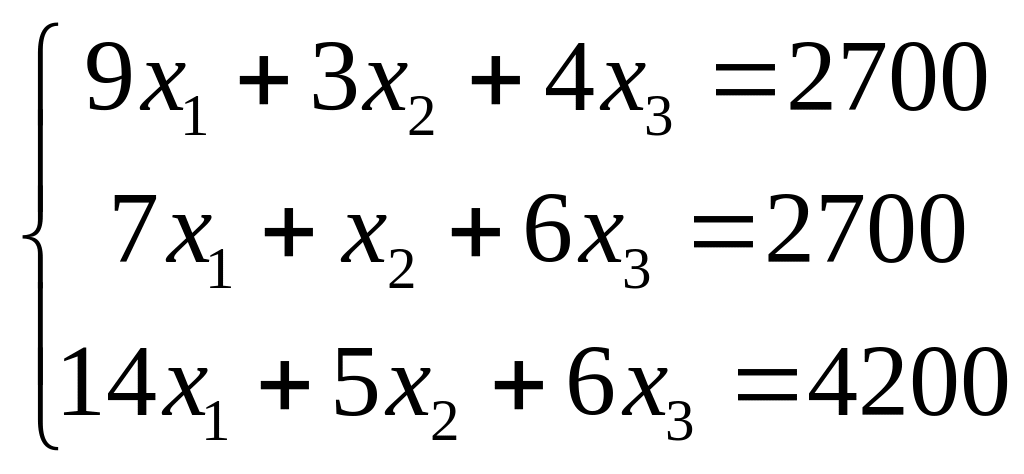Розв’язавши цю систему, знайдемо . Це означає, що підприємство щоденно виробляє 100 виробів виду α, 200 виробів виду β, 300 виробів виду γ.

Приклад.

Два заводи виробляють апарати для двох підприємств. Підприємствам необхідно отримати 120 і 80 апаратів відповідно. Перший завод випустив 150 апаратів, а другий 50. Витрати на перевезення апаратів кожного із заводів кожного підприємства такі:

Завод	Витрати на перевезення, грош. од.
	1	2
1	10	20
2	5	25

Мінімальні витрати на перевезення становлять 2850 грош. од. Знайти оптимальний план перевезення апаратів.

Розв’язування.

Позначимо – кількість апаратів, що надходять з і-го заводу до j-го підприємства. Тоді ми можемо скласти таку систему:

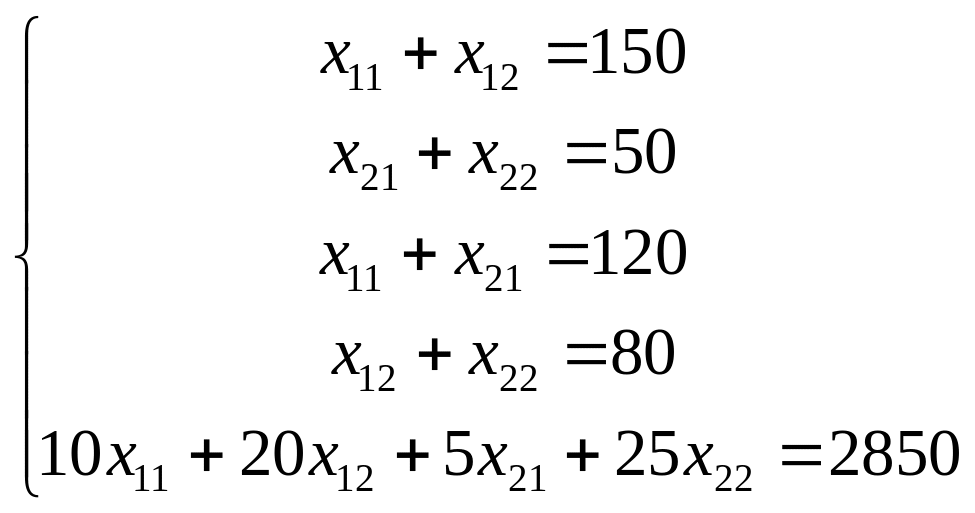
Розв’язавши систему, наприклад методом Гаусса, знайдемо .

Модель Леонтьєва міжгалузевого балансу.

Валову продукцію кожної галузі n- галузевої економіки позначимо (і = 1,2,…, n). Частина цієї продукції може використовуватись для міжгалузевих потреб, позначимо її (j = 1,2,…,n(обсяг продукції і-тої галузі, використаної в j-й галузі), а інша частина – для задоволення скінченного ринкового попиту у_і (товарна продукція і-ї галузі. Цей розподіл валового продукту можна описати таблицею міжгалузевих зв’язків:

Галузь матеріального виробництва	Обсяг валової продукції	Міжгалузеві потоки в галузі	Кінцевий продукт
		1,2…n
1	x1	Х11 Х12 …x1n	у1
2	x2	Х21 Х22 …x2n	у2
…	..	… … …. …	…
n	Xn	Х1n Х2n … xnn	yn

та системою балансових рівнянь:

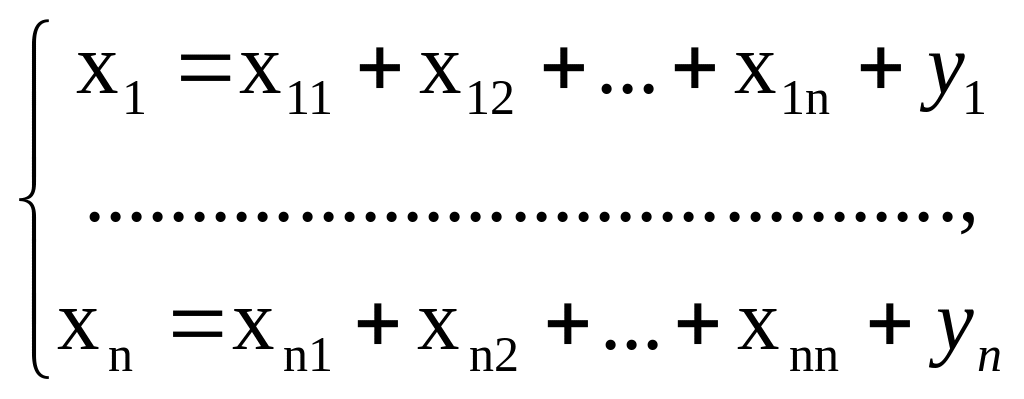
кожне з яких відображає міжгалузеві зв’язки галузевої економіки.

Нормативні коефіцієнти, що дорівнюють кількості продукції ї галузі, використаної на виробництво одиниці продукції ї галузі, позначимо . Вони утворюють матрицю прямих витрат А:

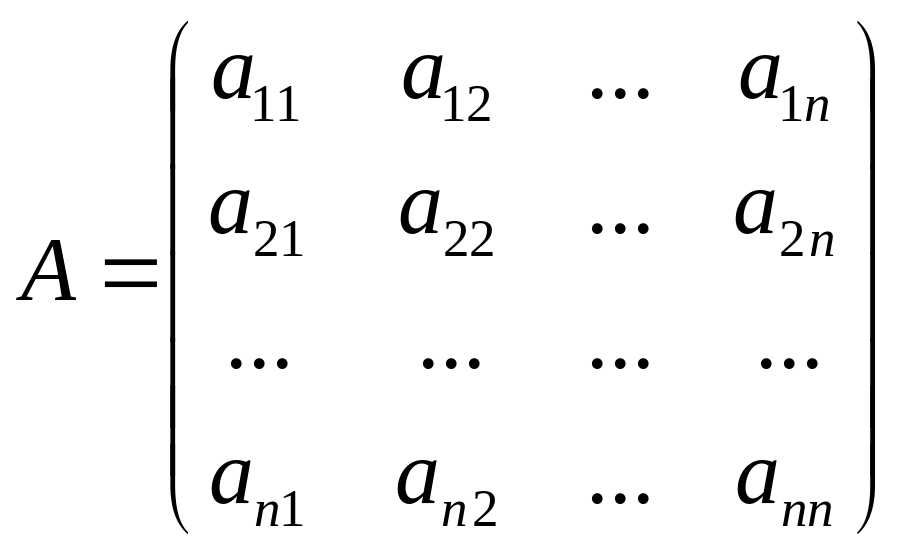
Цю матрицю також називають технологічною матрицею галузевої економіки. Для незмінної технології виробництва матриця прямих витрат стала і завжди відома на запланованій період.

Враховуючи те, що , балансові рівняння набувають вигляду:

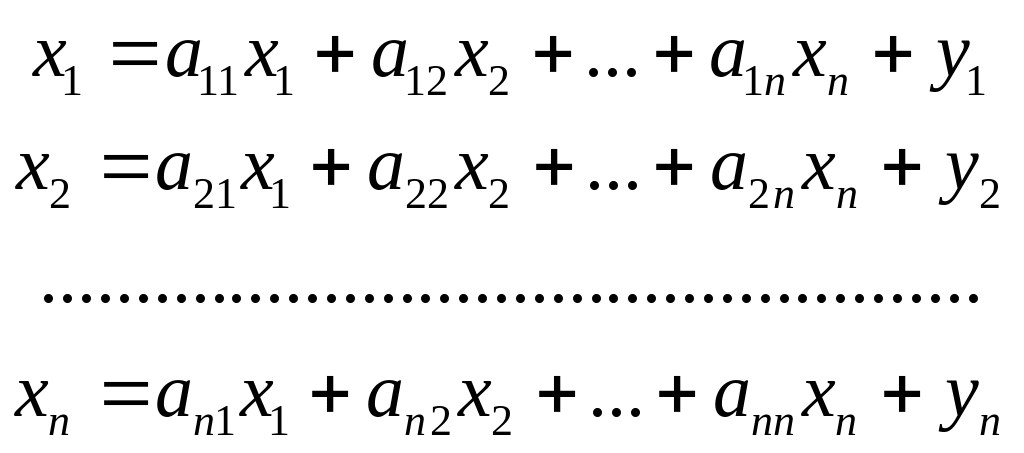
У матричному вигляді одержимо балансове співвідношення моделі Леонтьєва

Де - вектор валового продукту, 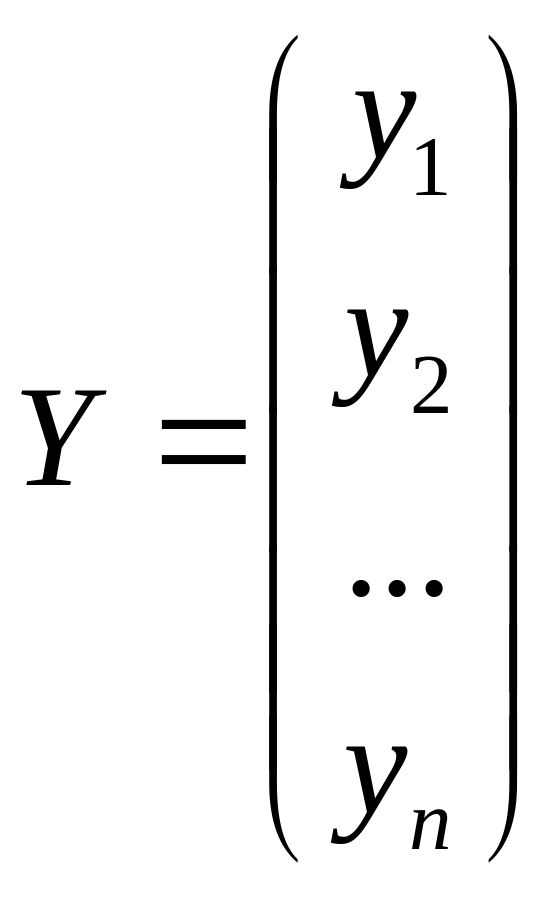- вектор товарної продукції

Матрицю називають матрицею повних витрат (сукупного споживання). Матрицю називають матрицею повних внутрішніх витрат, а матрицю - матрицею побічних витрат. Кожний елемент матриці В означає сукупній продукт ї галузі, необхідний для забезпечення випуску одиниці товарної продукції ї галузі.

Матрицю називають продуктивною, якщо для довільно скінченного вектору існує невід’ємний розв’язок системи . У цьому випадку і модель Леонтьєва називають ефективною, економіку – рентабельною. Одним із критеріїв продуктивності матриці А є:

Матриця А з невід’ємними елементами продуктивна, якщо максимум сум елементів її стовпців не перевищує одиниці, причому хоча б для одного стовпця сума елементів строго менша одиниці.

Рівняння міжгалузевого балансу можна використовувати у двох задачах. У першій, коли відомий вектор валового випуску Х, потрібно знайти вектор попиту Y. У другій рівняння міжгалузевого балансу використовується з метою планування: на деякий період(наприклад рік) потрібно знайти валовий випуск продукції кожної галузі для задоволення міжгалузевих потреб та запланованого вектору попиту Y.

Приклад 5.

Таблиця 2 містить дані балансу трьох галузей промисловості за деякий період умов. грош. од. Треба знайти обсяг валового випуску продукції, якщо кінцевий продукт по галузях збільшити відповідно до 200, 70, 100 од.

Табл.2

Галузь виробництва	Споживання			Вектор попиту	Валовий випуск
	1	2	3
1 2 3	5 10 17	40 10 5	30 25 3	125 55 75	200 100 100

Розв’язування.

Користуючись формулою для коефіцієнтів прямих витрат знайдемо матрицю прямих витрат

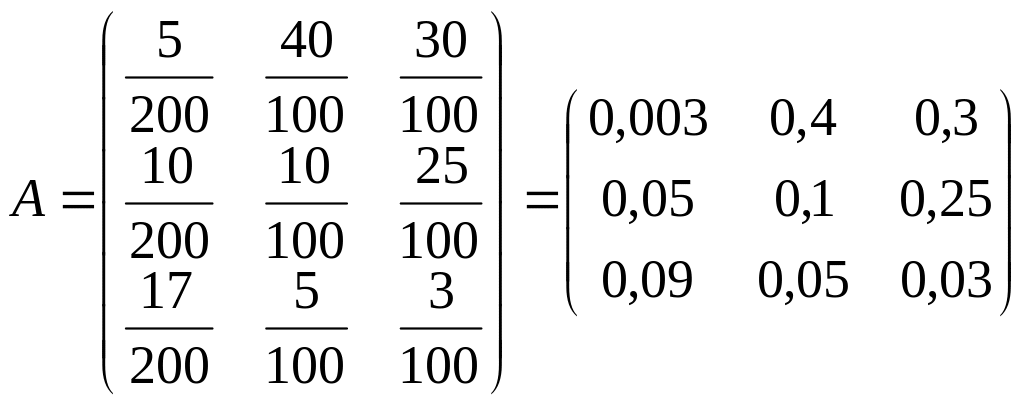
Далі записуємо матрицю Е-А: 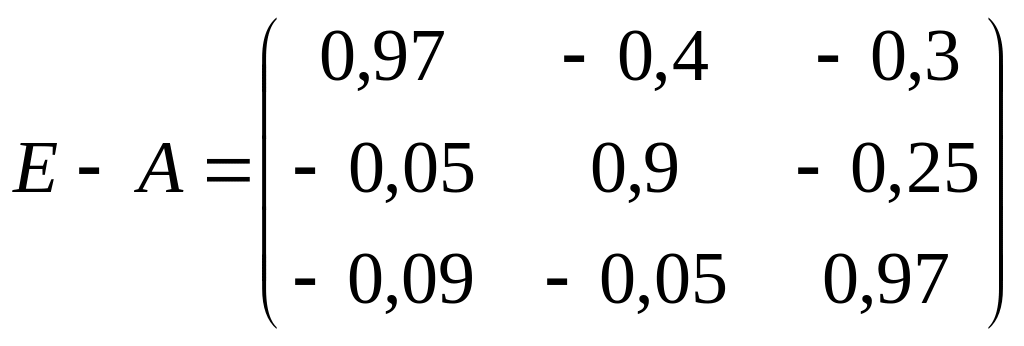і знаходимо обернену до неї матрицю повних витрат . Визначник матриці Е-А , отже

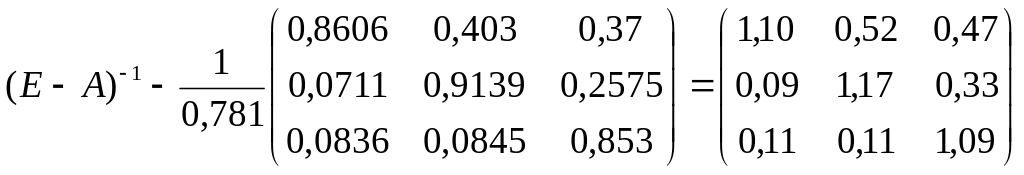
Валовий випуск необхідний для забезпечення нового товарного продукту одержимо із співвідношення

.

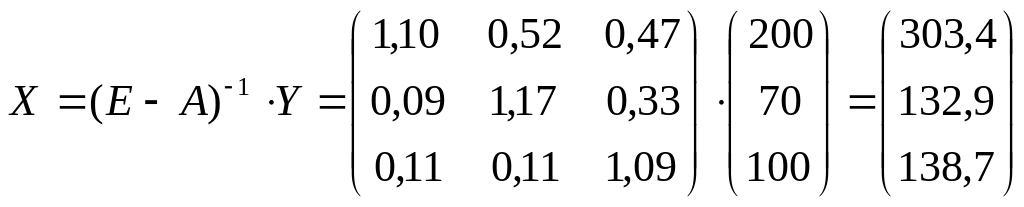Отже валовий випуск у першій галузі треба збільшити на 103,4 умов. од., у другій – на 32,9 умов. од. і у третій на 38,7 умов. од.

Лінійна модель обміну(модель міжнародної торгівлі)

Припустимо, що на встановлення торгівельних зв’язків з бюджетів n країн виділено кошти у кількостях . Нехай частка , яку та країна витрачає на закупівлю товарів у тої країни. Вважатимемо, що всі виділені кошти кожної країни витрачаються або на внутрішньому ринку, або на імпорт товарів. Остання умова забезпечує рівність , . Матрицю з елементів називають структурною матрицею торгівлі:

.

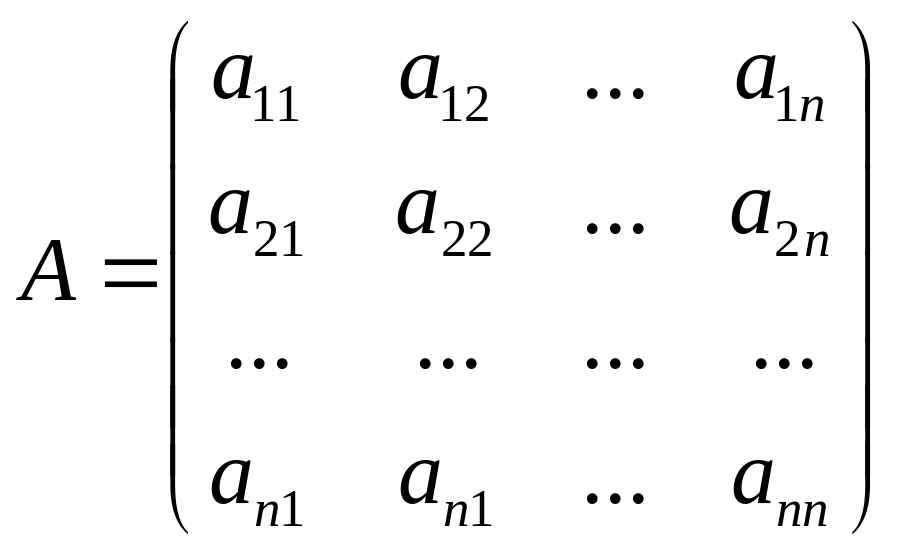Для тої країни виторг дорівнює

Бездефіцитність торгівлі для кожної країни забезпечується умовою , . З економічної точки зору нерівність неможлива (всі країни не можуть одночасно отримувати прибуток), тому умова збалансованої торгівлі набуває вигляду , .

Нехай , тоді умову збалансованої торгівлі можна записати у матричній формі:

, або .

Остання рівність дозволяє визначити Х.

Приклад.

Структурна матриця торгівлі трьох країн має вигляд:

Знайти співвідношення коштів цих країн для збалансованої бездефіцитної торгівлі. Якими повинні буті величини коштів за цієї умови, якщо сума їх задана .

Розв’язування.

Розв’яжемо рівняння . Маємо:

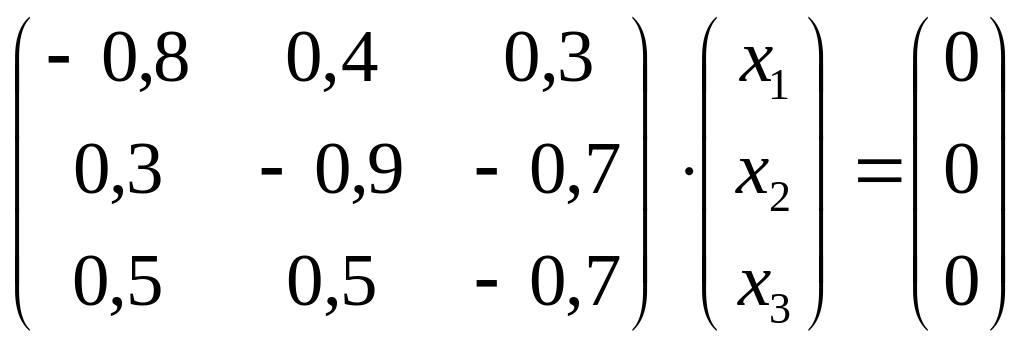, або

Використовуємо метод Гаусса для знаходження розв’язку одержаної однорідної системи рівнянь. Одержимо: , , . Це означає, що збалансованість торгівлі данник країн може бути досягнута тільки у випадку коли бюджети знаходяться у відношенні . Підставимо знайдені значення у задану суму бюджетів, щоб визначити величину . Звідси остаточно одержимо шукані величини коштів країн за умови бездефіцитної торгівлі: , , .