Тема 3 Системи лінійних рівнянь

3.1 Основні поняття

Означення: Системою m лінійних рівнянь із n невідомими або лінійною системою, називають систему рівнянь

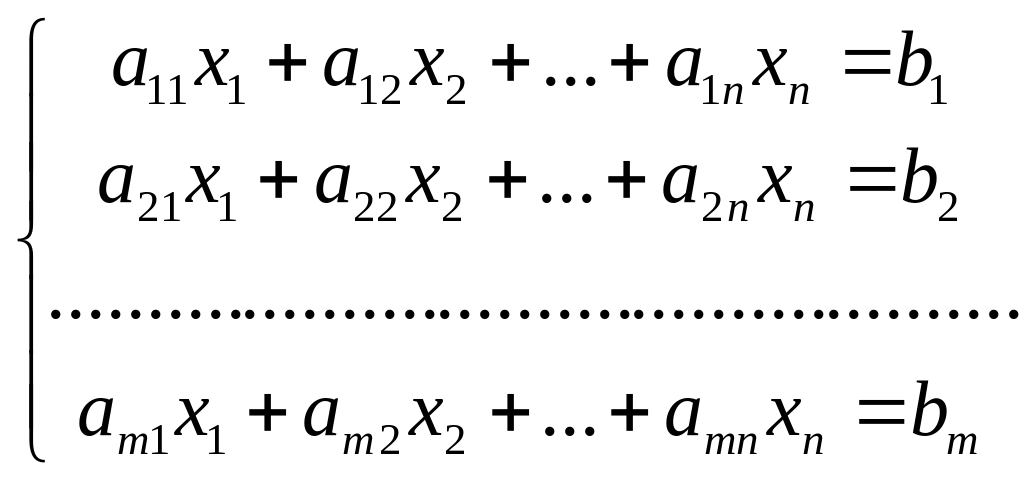(1)

Числа називають коефіцієнтами, а числа – вільними членами системи (1).

Лінійну систему називають однорідною, якщо всі вільні члени дорівнюють нулю. Якщо ж серед вільних членів є нульові, то лінійну систему називають неоднорідною.

• Означення : Розв’язком системи лінійних рівнянь (1) називають упорядковану сукупність чисел 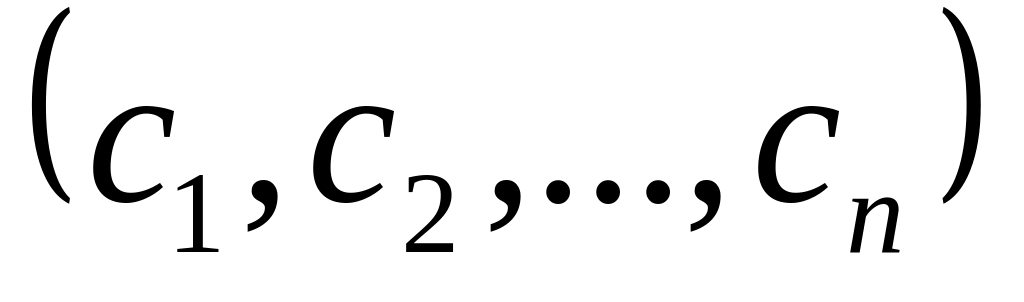, підставлення яких замість відповідних невідомих перетворює кожне з рівнянь системи (1) на тотожність.

• Означення: Систему (1) називають сумісною, якщо вона має принаймні один розв’язок. Якщо система (1) не має розв’язків, то її називають несумісною. Якщо систему, яка має тільки один розв’язок, називають визначеною. Якщо сумісна система має нескінченну кількість розв’язків, її називають невизначеною.

• Означення: Дві системи вважаються еквівалентними, якщо множини їхніх розв’язків однакові.

Зокрема, дві несумісні системи еквівалентні.

Подамо систему (1) у матричному вигляді.

Матрицю 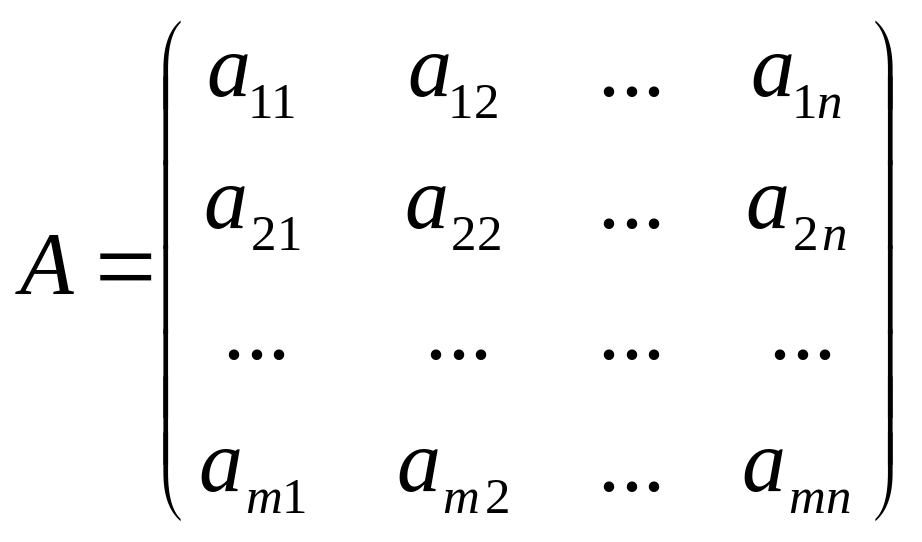називають основною матрицею, а

матрицю 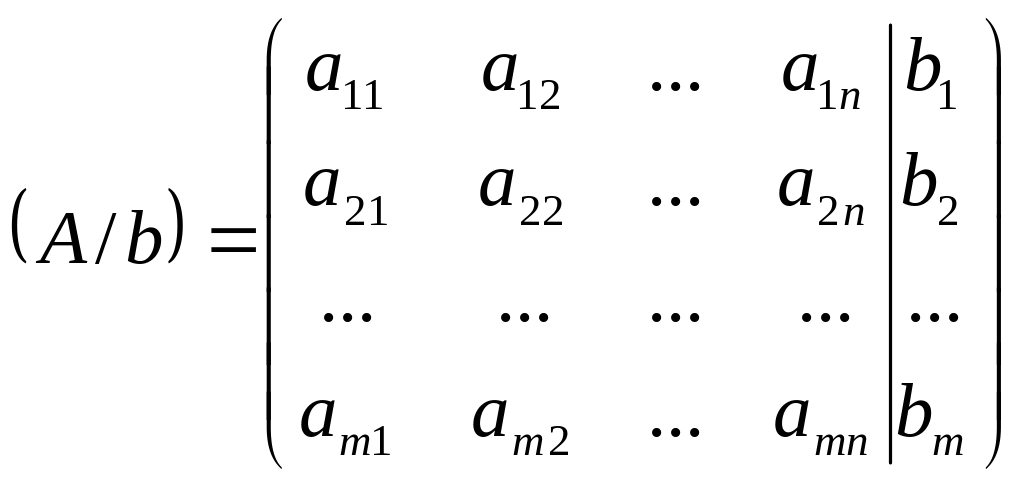- розширеною матрицею системи.

Позначимо через X та B матриці-стовпці 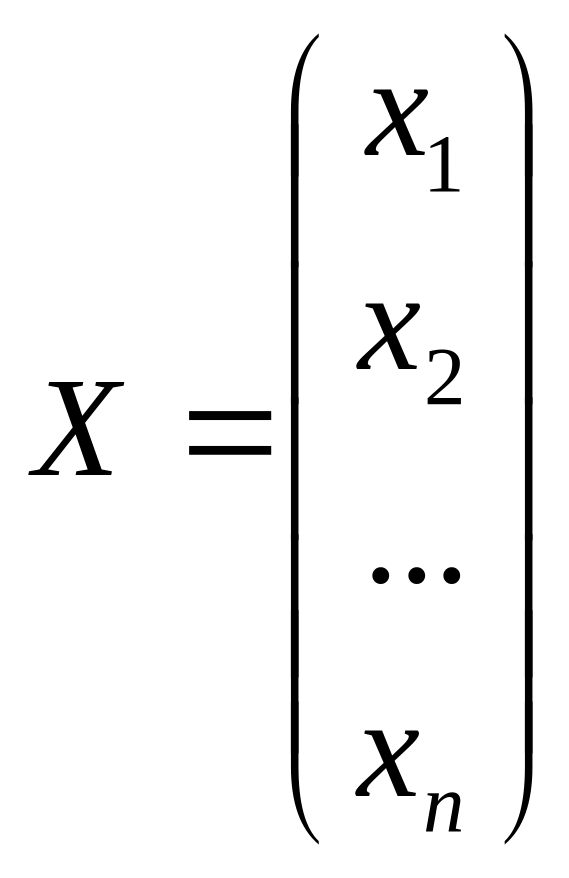, , складені з невідомих і вільних членів. Тоді система (1) набере вигляду

. (2)

Такий запис називають матричним.

3.2 Критерій сумісності слар

Розв’язуючи ту чи іншу систему рівнянь, як правило, насамперед зясовують, чи сумісна вона, й потім уже знаходять усі її розв’язки.

Нехай задано систему лінійних рівнянь (1), у якій число невідомих не менше за кількість рівнянь . Питання про сумісність такої системи розв’язує наступна теорема.

ТЕОРЕМА (Кронекера - Капеллі)

Система лінійних рівнянь сумісна тоді й лише тоді, коли ранг основної матриці системи дорівнює рангу розширеної матриці цієї системи.

За цією теоремою, якщо ранги основної та розширеної матриць не рівні, то система несумісна й немає сенсу її розв’язувати. Якщо ранги матриць рівні, то система сумісна.

Для сумісних систем лінійних рівнянь можливі такі випадки.

1. Якщо ранг матриці сумісної системи дорівнює числу невідомих, тобто 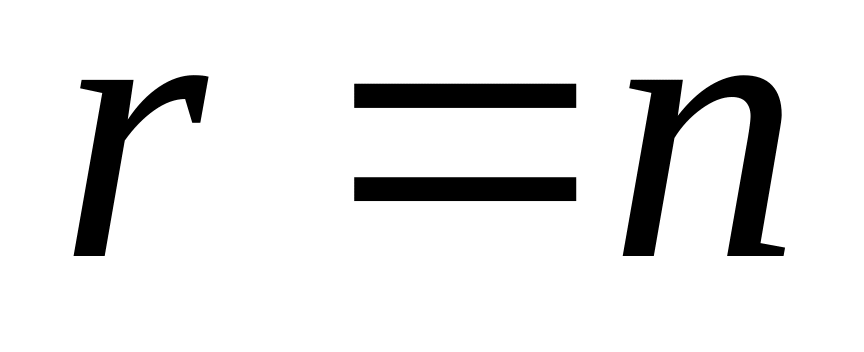, то система (1) має єдиний розв’язок.

Справді, в цьому разі система (1) має квадратну не вироджену матрицю порядку і, за теоремою Крамера, існує єдиний розв’язок цієї системи, тобто система визначена.

2. Якщо ранг матриці сумісної системи менший від числа невідомих, тобто 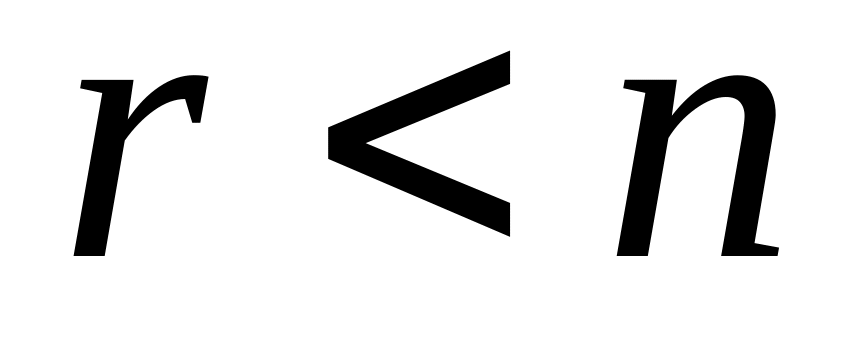, то система невизначена й має нескінченну кількість розв’язків.

Нехай ; тоді невідомих називаються основними, або базисними, якщо визначник матриці з коефіцієнтів при цих невідомих (тобто базисний мінор) відмінний від нуля. Решта невідомих називаються неосновними, або вільними. Можна показати, що базисні невідомі лінійно виражаються через вільні невідомі. Оскільки вільні невідомі можуть набути довільних значень, то в цьому разі система буде невизначеною.

Розв’язком системи (1), в якому всі неосновних невідомих дорівнюють нулю, називають базисним.

Приклад. Розв’яжемо систему рівнянь

Запишемо основну й розширену матриці системи:

, .

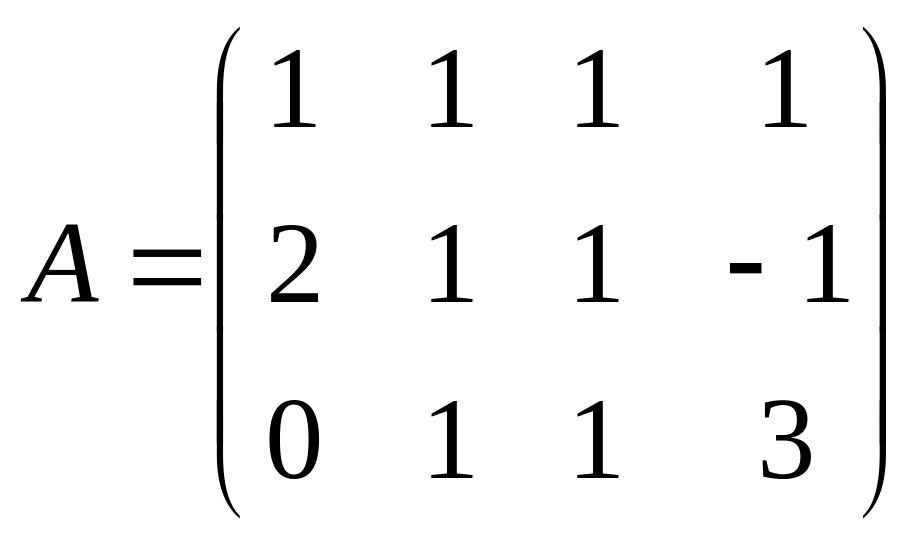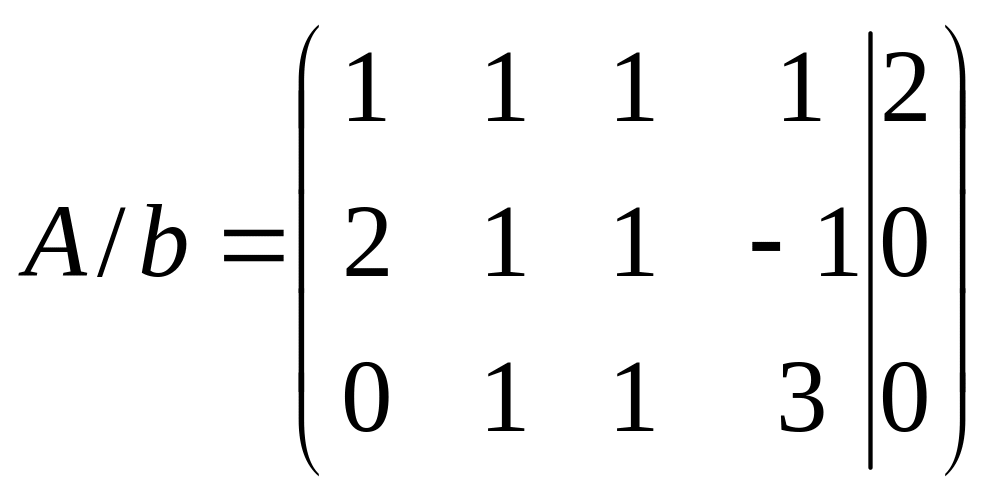Їхні ранги відповідно. Отже, система несумісна.

Приклад. Розв’яжемо систему рівнянь

Ця система сумісна, оскільки , причому ранг матриці менший від числа невідомих. Отже, система має безліч розв’язків. Мінор , тому обмежимось лише двома рівняннями, а візьмемо за вільні невідомі. Перенесемо вільні невідомі в праві частини перших двох рівнянь:

Розв’язуючи цю систему, дістанемо

Отже, дана система має розв’язки

,

де – довільні числа.