2 Розрахунково-графічна робота «Моделювання обрису поверхні обертання»
Мета роботи – опанування методу побудови обрису поверхні обертання за заданими твірною лінією та віссю обертання, розвиток просторової уяви шляхом відтворення конкретної поверхні за заданими проекціями геометричної частини її визначника.
Умова роботи:
Побудувати проекції обрису поверхні обертання.
Порядок виконання.
1. На форматі А3 накреслити завдання, використовуючи його у «книжковому» положенні. Наприклад :
2. Визначаємо на твірній m точку, що знаходиться на мінімальній відстані від осі I. Для заданої твірної це буде точка 1 (11,12).
3
.
Будуємо проекції паралелі (горла), яку
утворює внаслідок обертання навколо
осі і
точка 1.
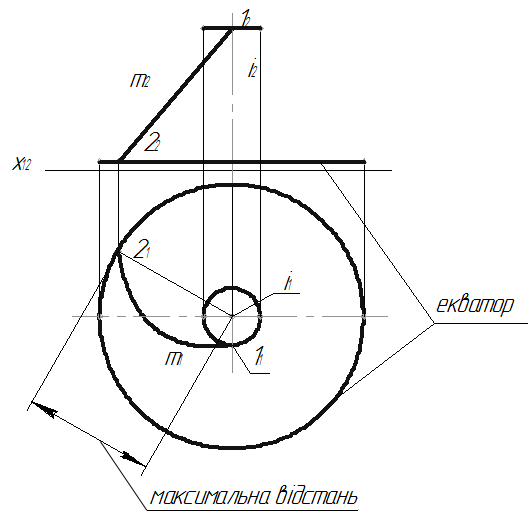4.
Визначаємо на твірній
m
точку,
що знаходиться на максимальній відстані
від осі I.
Для заданої твірної це буде точка 2
(21,22). Така точка внаслідок обертання
утворить паралель, що матиме назву
екватора.
5. Визначаємо на твірній декілька точок та будуємо відповідні проміжні паралелі, які утворюють визначені точки. До таких точок перш за все відноситься точка 3 (31,32).
6. З’єднаємо плавною кривою лінією крайні точки побудованих паралелей, отримуючи таким чином обрис поверхні обертання на фронтальній площині, або головний меридіан. На горизонтальній площині проекцій обрисовими лініями такої поверхні є проекції у вигляді кіл горла та екватора.
3 Розрахунково-графічна робота «переріз поверхні площиною окремого положення»
Мета роботи – засвоїти теорію та алгоритми розв’язання третьої позиційної задачі – визначення проекцій ліній перерізу поверхонь площинами, шляхом розв’язання двох задач.
Умова роботи:
Побудувати проекції лінії перерізу поверхонь заданими площинами окремого положення.
Визначити натуральні величини фігур перерізів.
Порядок виконання:
Задача №1 (Побудова перерізу поверхні обертання)
1
.
Накреслити умову на форматі А3. Наприклад,
задана поверхня обертання
та
горизонтально-проекціювальна площина
α
(α1):
2. Позначити характерні точки перерізу: т.1 і т. 5 належать екватору, т.4 і 4' – головному меридіану, т. 2 і 2' – меридіану, т.3 і 3' – найменший за розмірами паралелі.
3. Побудувати фронтальні проекції позначених точок за умови, що:
точки 1 і 5 належать екватору, тому їх фронтальні проекції визначають за допомогою проведення ліній зв’язку;
точки 4 і 4' належать головному меридіану, тому їх фронтальні проекції також визначають за допомогою проведення лише ліній зв’язку;
точки 3 і 3' належать найменший паралелі, тому для визначення їх фронтальних проекцій будують допоміжну паралель радіусу r, відповідним проекціям яких і належать шукані проекції точок 3 і 3';
т очки 2 і 2' належать меридіану, для визначення їх фронтальних проекцій будують допоміжні паралелі радіусу R, відповідним проекціям яких належать шукані проекції точок 3 і 3';
4. Шуканий переріз має форму замкненої кривої лінії, проекції якої отримують шляхом сполучення однойменних проекцій побудованих точок перерізу.
5. Натуральну величину перерізу можна визначити за допомогою додаткової площини проекцій П4:
Порядок виконання:
Задача №2 (Побудова перерізу лінійчатої поверхні):
Накреслити умову на форматі А3. Наприклад, задана лінійчата поверхня (еліптичний конус) та фронтально-проекціювальна площина α (α2).
2. Позначити фронтальні проекції опорних точок перерізу:
т.1 і т.2 – точки, що належать напрямному колу, т.3 – належить обрисовій твірній;
т.4 - точка, що належить обрисовій твірній SA для горизонтальної проекції поверхні.
3 . Побудувати горизонтальні проекції точок 1, 2, 4 за допомогою проведення ліній зв’язку.
4. Для визначення горизонтальної проекції опорної точки перерізу т.3 необхідно спочатку побудувати горизонтальну проекцію твірної SB, а потім визначити проекцію т.3 за допомогою відповідної лінії зв’язку.
5. Шуканий переріз за формою є незамкнена крива 2-го порядку. Тому для її побудови використана ще одна точка – т.5, яка належить проміжній твірній SC. Шляхом сполучення однойменних проекцій точок отримуємо відповідні проекції шуканої кривої перерізу.
6. Натуральну величину перерізу можна визначити шляхом обертання перерізу до зайняття ним горизонтального положення.
