1.2.3 Дифракція плоских хвиль на дифракційній решітці

У найпростішому вигляді дифракційна решітка являє собою ряд прозорих щілин однакової ширини a, поділених однаковими непрозорими смугами шириною b (Рис. 3).

Рис. 3

На решітку нормально падає пучок паралельних монохроматичних променів. Промені, що дифрагували, далі збираються лінзою L і інтерферують. Таким чином, ми маємо накладення двох процесів - дифракції від кожної окремої щілини і інтерференції променів від усіх щілин. Напрямки мінімумів, визначені для однієї з щілин, збігаються з напрямками мінімумів, утворених кожною щілиною окремо. Також додаються мінімуми, що виникають при інтерференції хвиль, що виходять з різних щілин.

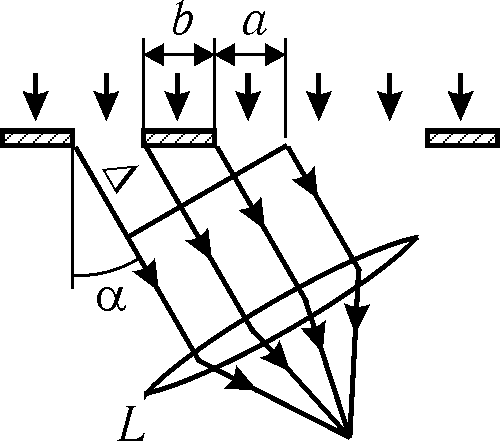
Якщо ж вибраний напрямок такий, що різниця ходу двох відповідних¹ променів від двох сусідніх щілин (рис.3) дорівнює цілому числу довжин хвиль, то і для всіх інших щілин різниця ходу буде також рівнятися цілому числу довжин хвиль. Їх накладання приведе до утворення дифракційного максимуму. Умова максимуму інтерференції для цих хвиль буде = k (k – ціле число, порядок спектру). З міркувань геометрії

.

(4)

Тоді позначив a + b = ℓ, (період дифракційної решітки) одержимо умову максимуму для дифракційної решітки:

.

(5)

Амплітудні значення електричних векторів, що виходять від усіх щілин, у максимумі додаються , а в зв’язку з тим, що інтенсивність світла пропорційна ,

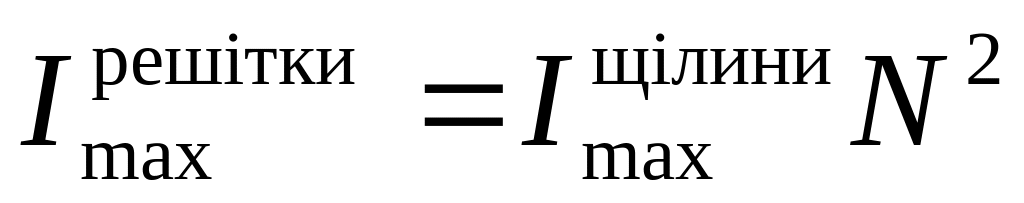.	(6)
1 Відповідні промені це такі промені, які випромінюються із симетричних точок сусідних щілин.

Рис.4

Світлосила решітки пропорційна квадрату числа щілин і значно вище світлосили окремої щілини. Це дозволяє широко використовувати дифракційні решітки для розкладання складного світла на спектр. На рис.4 схематично показані спектри, отримані при використанні дифракційної решітки.

Нульовий максимум не кольоровий, білий, а далі в обидві сторони йдуть спектри 1-го, 2-го … порядків. У кожному із спектрів дифракційні максимуми для фіолетових променів спостерігаються при менших значеннях кутів, ніж для червоних (тому що _ф < _к, див. формулу (5)).

2 ЕКСПЕРИМЕНТАЛЬНА ЧАСТИНА

2.1 Ціль роботи

Визначення періоду дифракційної решітки за допомогою лазера з відомою довжиною хвилі.

2.2 Прилади і приналежності

Дифракційна решітка з невідомим періодом, рубіновий лазер з довжиною хвилі λ = 700 нм, лінійки.

2.3 Експериментальна установка

Рис.5

На рис.5 показана схема установки. Джерелом світла, що дає паралельний пучок променів, є лазер L. Лазерний промінь падає на дифракційну решітку R, після чого дифрагує – розділяється на декілька променів – дифракційних максимумів декількох порядків. Дифраговані промені потрапляють на екран, відхилившись на кут від початкового напрямку. Відстань від дифракційної решітки до екрана у вимірюється лінійкою Л2, відстань дифрагованого променя від центра екрану х вимірюють лінійкою Л2. Скориставшись формулою (5) можна розрахувати період решітки для кожного дифрагованого променя:

.

(7)

k – порядок спектру – це просто номер променя, якщо починати відлік від центрального максимуму (для нього k=0). З рис. 5 можна бачити, що , тоді:

.

(8)