3. Дії над векторами в координатній формі

Для того, щоб операції над векторами звести до операцій над числами, розглянемо вектори в системі координат. Очевидно (див.рис.16).

, в просторі .

Довжина вектора або в просторі . Якщо початок вектора міститься в т. , а кінець – в т. , то з рис.12 видно

, , а в просторі ще ,

тобто , а довжина

, що відповідає формулі відстані між т. та т. . Напрям довільного вектора визначається напрямними кутами , які утворює вектор з осями координат , , , .

Формули для напрямних косинусів будуть:

, , .

У прямокутній системі координат для векторів та буде:

, ,

, та - колінеарні, то .

Добутки векторів

§1. Скалярний добуток векторів

Нехай, в просторі дано два вектори та , що утворюють між собою кут .

Означення 1. Скалярним добутком двох векторів та називається число, що дорівнює добуткові довжин цих векторів на косинус кута між ними, яке позначається або :

. (1)

Якщо точка під дією постійної сили здійснює прямолінійне переміщення , вектор якого утворює кут з напрямом сили , то робота , виконана при цьому силою буде рівна , тобто скалярному добутку вектора сили на вектор переміщення.

Оскільки добуток ,

а , то

, (2)

тобто скалярний добуток двох векторів дорівнює добутку модуля одного з них на проекцію другого на вісь, що визначається першим вектором.

Властивості скалярного добутку:

1. ;

2. ;

3. ;

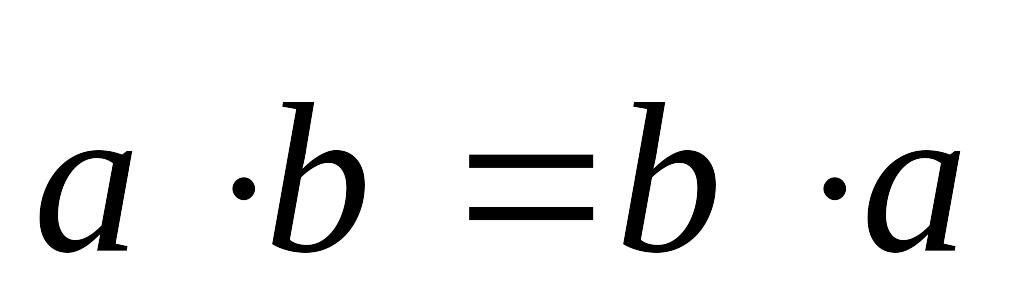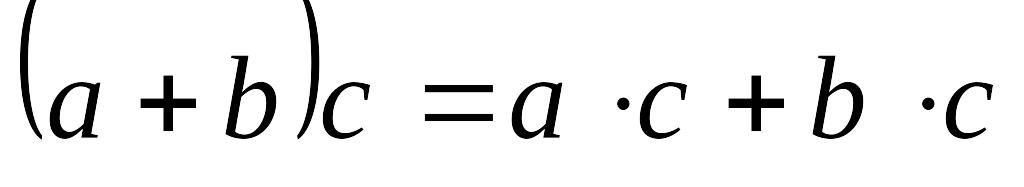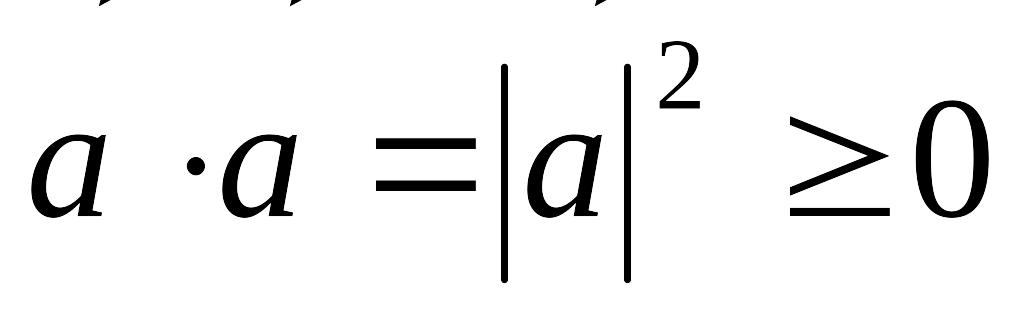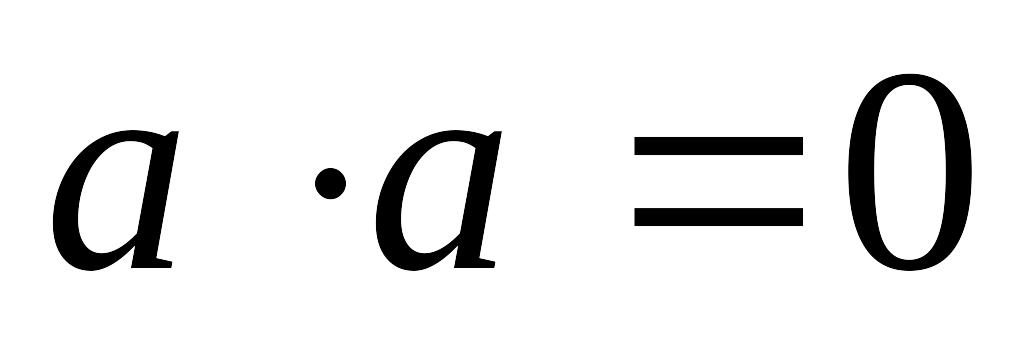4. , якщо , то .

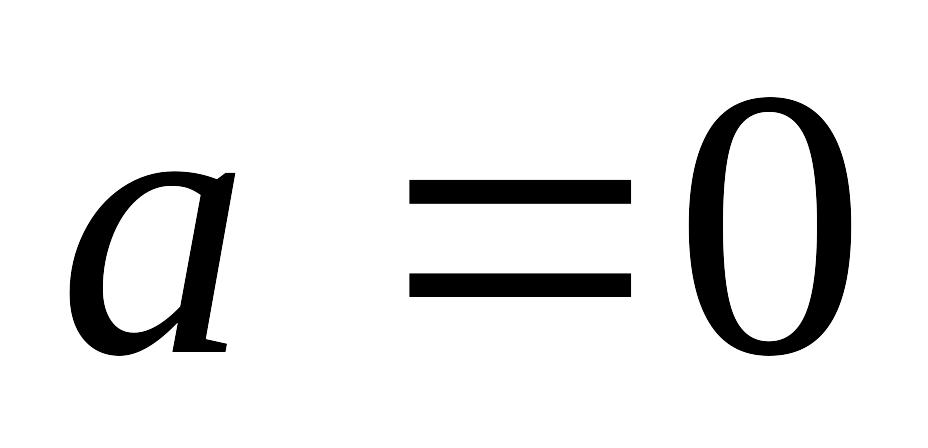Доведення цих властивостей пропонуються для самостійної роботи.

Теорема 1. Вектори та взаємно перпендикулярні тоді й тільки тоді, коли їх скалярний добуток дорівнює нулю.

Доведення. Необхідність. Нехай вектори та перпендикулярні . Тоді .

Достатність. Нехай, . Якщо , то , тобто . Якщо ж один з векторів рівний , то внаслідок невизначеності напряму нульового вектора можна вважати, що .

Нехай вектори та задані своїми координатами , , тобто , . Тому в силу властивостей скалярного добутку і теореми 1, отримують:

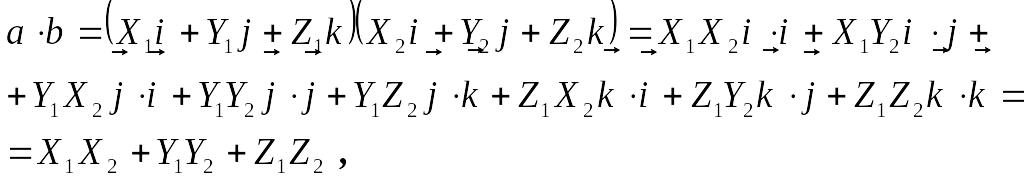
тобто . (3)

Скалярний добуток векторів дорівнює сумі добутків їх одноіменних координат. Із формули (3) і теореми 1 випливає, якщо , то .

З формули (1) легко отримати 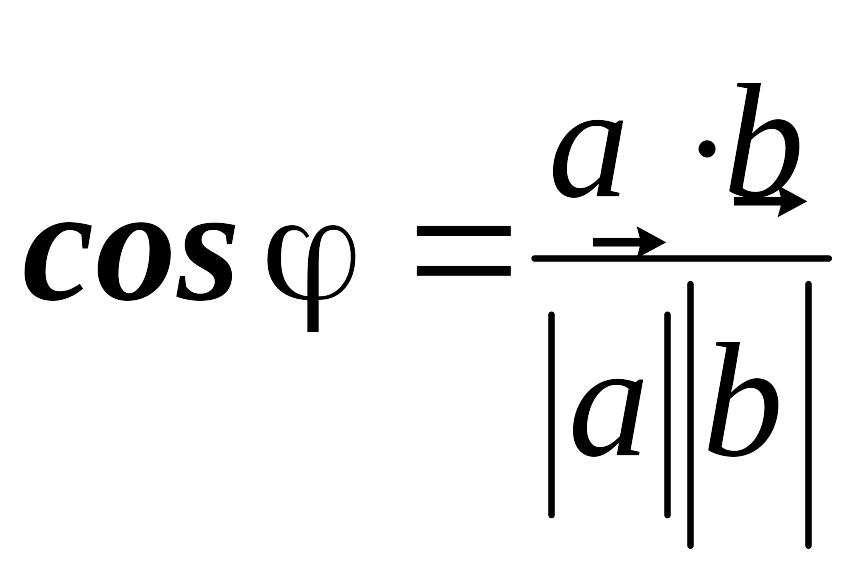, або в координатній формі

.

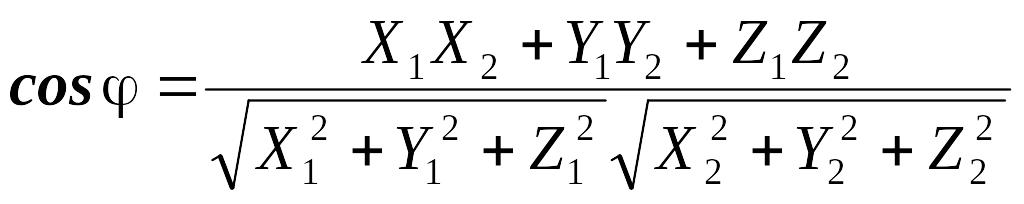§ 2. Векторний добуток векторів

Три вектори в просторі утворюють упорядковану трійку векторів, якщо вказано, який з них перший, який – другий, який – третій. Записують вектори в порядку проходження.

Трійка не компланарних векторів називається правою (лівою), якщо вектори орієнтовані так само, як і вектори правої (лівої) систем координат (див. лк.3), тобто з кінця вектора видно поворот від першого вектора до другого вектора проти годинникової стрілки (за годинниковою стрілкою), при умові, що початки векторів віднесені до спільної точки.

Означення 1. Векторним добутком вектора на вектор називається вектор, що позначається або , який:

1. перпендикулярний до кожного з векторів та ;

2. разом з векторами та утворює праву трійку векторів 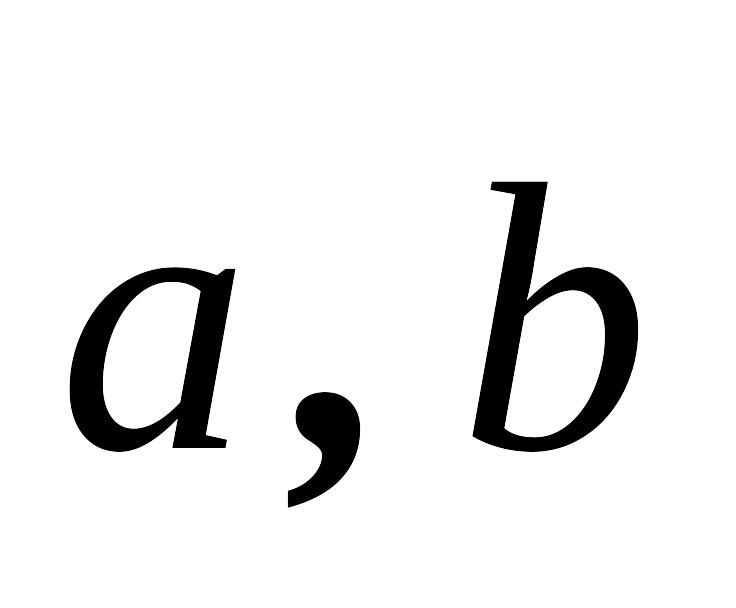, (рис.1);

3. має довжину, що дорівнює добутку довжини векторів та на синус кута між ними, тобто .

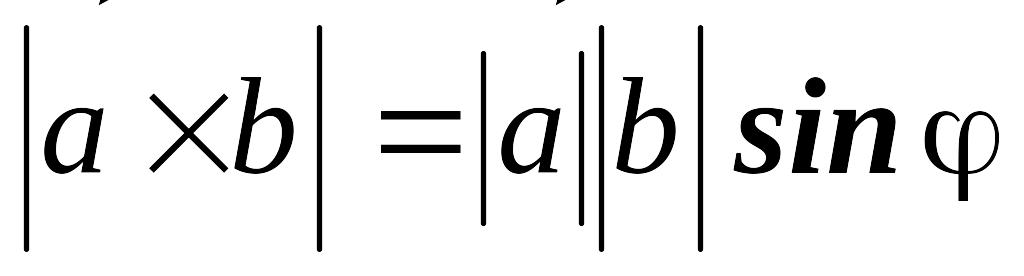З означення векторного добутку випливає його геометричний зміст: модуль векторного добутку векторів та дорівнює площі паралелограма, побудованого на цих векторах

.

Властивості векторного добутку:

1. 

2. 

3. 

4. .

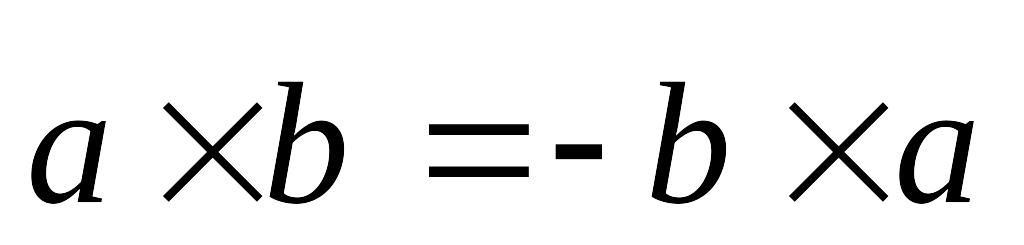
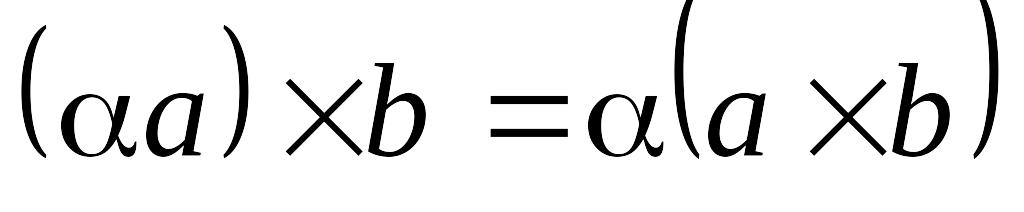
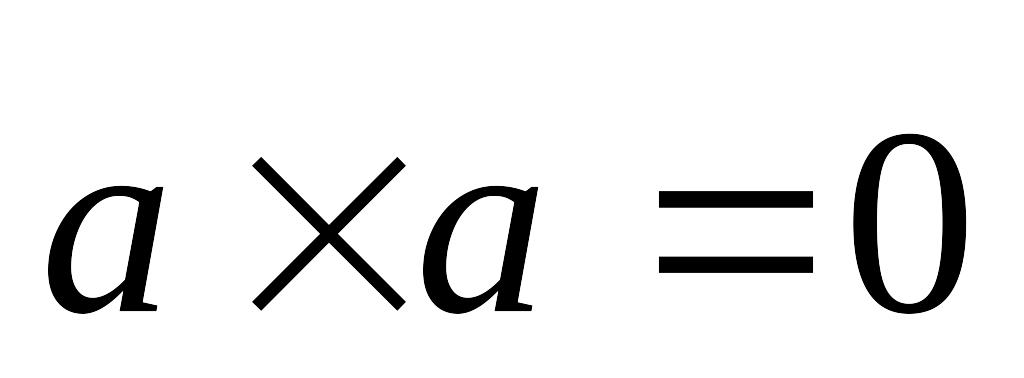
Теорема 2. Вектори та колінеарні тоді і тільки тоді, коли їх векторний добуток дорівнює нулеві.

Доведення. Якщо вектори та колінеарні , то . Якщо , і , то , тобто .

З властивостей векторного добутку і лінійних операцій над векторами випливає, що вектори можна перемножувати векторно за правилами алгебри скалярних величин, але, пам’ятаючи про порядок векторних множників.

Нехай вектори та задані координатами , , тобто , .

Перемножуючи їх векторно, одержують:

З означення векторного добутку для векторів одержують:

, , , .

Звідки , або, використовуючи означення визначника третього порядку, можна записати:

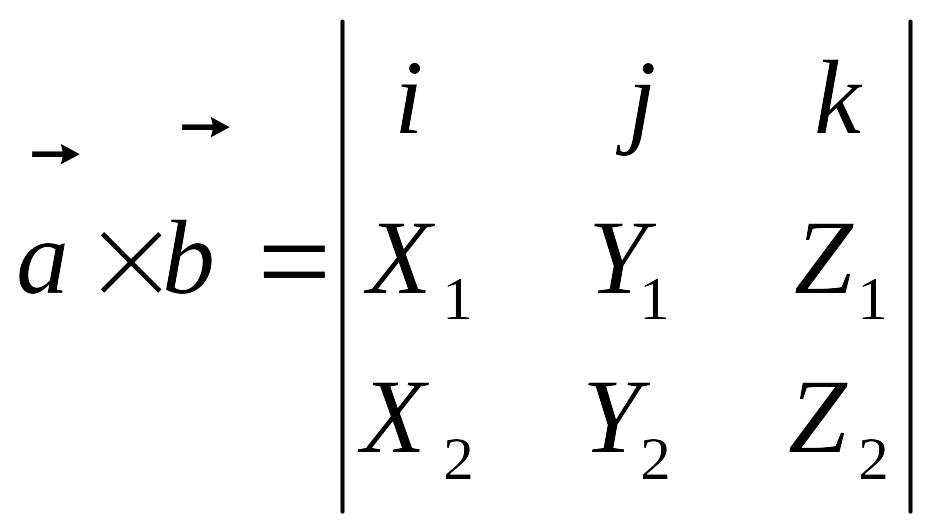. (4)

Якщо та колінеарні, то , тобто

, то , тобто, якщо вектори колінеарні, то їх координати пропорційні.