§6. Обернена матриця

Квадратна матриця називається невиродженою, якщо її визначник відмінний від нуля: , в протилежному випадку – виродженою.

Нехай задано квадратну матрицю . Матриця називається оберненою до матриці , якщо . Обернену матрицю позначають . Отже . Всяка невироджена матриця має обернену і для її побудови використовують слідуючий алгоритм:

,

тобто потрібно знайти , алгебраїчні доповнення кожного елемента матриці , знайдені алгебраїчні доповнення елементів рядка записати у відповідний стовпець (або знайти матрицю алгебраїчних доповнень елементів матриці , а потім її транспонувати) і так складену матрицю з алгебраїчних доповнень помножити на .

§ 7. Ранг матриці та його знаходження

1. Елементарними перетвореннями рядків матриці називаються такі операції:

а) Множення всіх елементів деякого рядка матриці на число .

б) Перестановка рядків матриці.

в) Додавання до всіх елементів деякого рядка матриці відповідних елементів іншого рядка, помножених на одне й те ж число.

г) Відкидання нульових рядків матриці.

Матриці, отримані одна з другої за допомогою скінченої кількості елементарних перетворень називаються еквівалентними і позначаються ~ .

Зауважимо, що ці ж самі елементарні перетворення можна виконувати і над стовпцями.

Прямокутна матриця називається ступінчатою, якщо перший, відмінний від нуля елемент її кожного рядка, починаючи з другого, розміщений правіше першого ненульового елементу попереднього рядка.

Квадратна ступінчаста матриця називається трикутною.

2. Рангом матриці називають найбільше число її лінійно незалежних рядків. Для знаходження рангу матриці зводять її до ступінчатого виду (відкидаючи нульові рядки), тоді її ранг рівний числу ненульових рядків відповідної ступінчатої матриці. Позначають ранг матриці або .

Системи лінійних алгебраїчних рівнянь

§ 1. Основні поняття

Системою рівнянь з невідомими або лінійною системою, називається сукупність рівнянь виду

(1)

де - задані числа. Числа називаються коефіцієнтами, числа - вільними членами. Якщо всі , то система однорідна, в протилежному випадку – неоднорідна.

Розв’язком системи називається впорядкована множина таких чисел , підстановка яких замість обертає в тотожність кожне рівняння системи.

Якщо система має розв’язок, то вона називається сумісною, в протилежному випадку – несумісною. Якщо ж сумісна система має єдиний розв’язок, то вона називається означеною, якщо ж більше одного розв’язку – то неозначеною.

Дві системи лінійних рівнянь називаються еквівалентними, якщо розв’язок однієї з них є розв’язком другої і навпаки. Дві несумісні системи вважаються еквівалентними.

Введемо матриці елементів, що входять в систему:

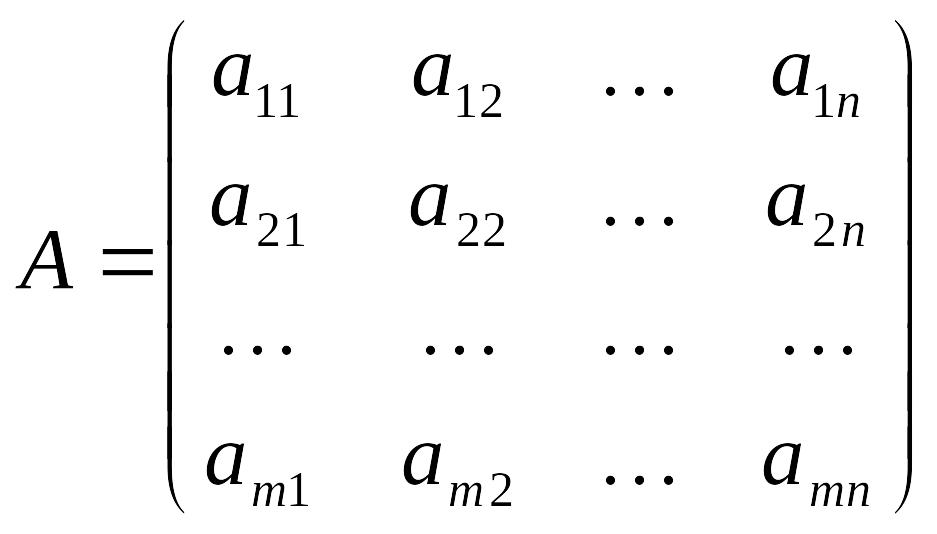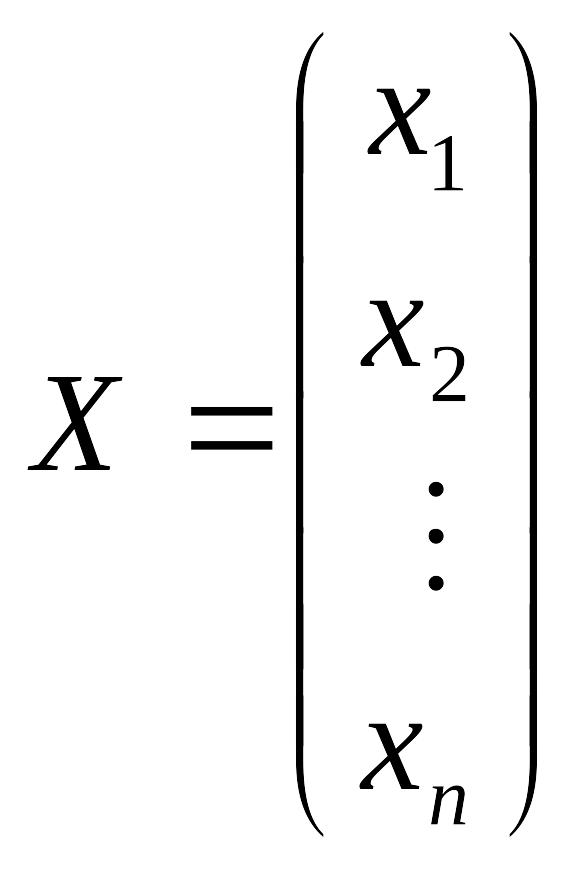; ; . (2)

Матриця , елементами якої є коефіцієнти при невідомих, називається головною матрицею системи; матриця - стовпець невідомих; - матриця-стовпець вільних членів системи. Очевидно, система запишеться в матричній формі:

.