
- •Аэрогидрогазодинамика. Учебное пособие для практических занятий
- •Isbn 5-696-00000-0 © Издательство юУрГу, 2014
- •Предисловие
- •Часть 1. Теоретические предпосылки и условия задач Тема 1. Аэродинамические силы и коэффициенты
- •Характерные размеры ла
- •Тема 2. Уравнения: неразрывности, импульса, Бернулли
- •Тема 3. Изэнтропические течения
- •Связь параметров торможения с числом м движущегося газа
- •Связь критических параметров с параметрами торможения
- •Тема 4. Скачки уплотнения
- •4.1. Прямые скачки уплотнения
- •4.2. Косые скачки
- •Тема 5. Сверхзвуковое обтекание тел вращения
- •5.1. Обтекание конуса сверхзвуковым потоком
- •5.2. Обтекание тел вращения с криволинейной образующей ( )
- •Давление в донной части
- •Аэродинамические коэффициенты для тел вращения
- •Тема 6. Гидростатика Основное уравнение гидростатики
- •Относительный покой
- •Силы давления жидкости на криволинейные поверхности
- •Тема 7. Критерии подобия
- •Тема 8. Путевые потери напора Течение вязкой жидкости по трубам
- •Уравнение Бернулли с учетом потерь давления на трение
- •Тема 9. Местные сопротивления. Истечения через отверстия и насадки
- •Истечение через диафрагму
- •Истечения через отверстия и насадки при постоянном напоре
- •Тема 10. Нестационарные течения
- •10.1 Неустановившиеся течения
- •10.2. Гидравлический удар в трубах
- •Часть 2. Решения задач Тема1. Аэродинамические силы и коэффициенты
- •Тема 2. Уравнения неразрывности, импульса, Бернулли
- •Тема 3. Изэнтропические течения
- •Тема 4.Скачки уплотнения
- •Тема 5.Обтекание тел
- •Тема 6. Гидростатика
- •Тема 7. Критерии подобия
- •Тема 8. Путевые и местные потери напора
- •Тема 9. Истечения через отверстия и насадки при постоянном напоре
- •Тема 10. Нестационарные течения
- •10.1 Неустановившиеся течения
- •10.2. Гидравлический удар в трубах
- •Приложения приложение №1. Параметры воздуха.
- •Приложение №2. Физические свойства газов.
- •Плотность некоторых газов при 00 и 760 мм.Рт.Ст.
- •Зависимость показателя адиабаты для воздуха от температуры
- •Приложение №3. Международная система единиц (си)
- •Библиографический список

Рис. 6.2. Объем тела давления
β
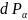
h
где – объем тела давления в направлении α. Это объем, заключенный внутри цилиндрической поверхности, образованной лучами, проведенными через каждую точку контура S в направлении α, и ограниченный, с одной стороны поверхностью S, а с другой стороны свободной поверхностью жидкости. (Цилиндрическая поверхность- это поверхность с параллельными образующими.)
(или
)
dS
Sα
dP



Из (6.11) вертикальная составляющая
 , (6.12)
, (6.12)
а для горизонтальной составляющей имеем
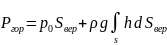 ,
(6.13)
,
(6.13)
где
 – статический момент площадки
– статический момент площадки
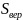 , а
, а
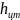 – центр тяжести
. Окончательно
– центр тяжести
. Окончательно
 (6.14)
(6.14)
(6.15)
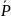 определится, как
определится, как
 а угол β ее наклона к вертикали
(рис. 6.3) – соотношением
а угол β ее наклона к вертикали
(рис. 6.3) – соотношением

Линия действия силы давления жидкости
Рассмотрим последовательно вопросы определения центра давления (положения линий действия) сил:

Линия действия силы
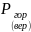 от
равномерно распределенного давления
p0 на
криволинейную поверхность S
проходит через центры тяжести площадок
от
равномерно распределенного давления
p0 на
криволинейную поверхность S
проходит через центры тяжести площадок
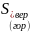 .
.
Линия действия
 проходит через центр тяжести тела
давления.
проходит через центр тяжести тела
давления.
Точка, через которую проходит
равнодействующая (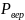 )
определяется из условия равенства
момента равнодействующей сумме моментов
ее составляющих (
)
определяется из условия равенства
момента равнодействующей сумме моментов
ее составляющих ( .
.
Аналогично определяется положение
линии действия для
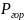 при условии, если известен центр давления
для
при условии, если известен центр давления
для
 .
Его определение в более общем случае
будет рассмотрено ниже.
.
Его определение в более общем случае
будет рассмотрено ниже.
Зная линии действия векторов и их
величины, легко находят линии действия
силы
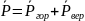 по схеме рис. 6.3.
по схеме рис. 6.3.
0


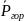
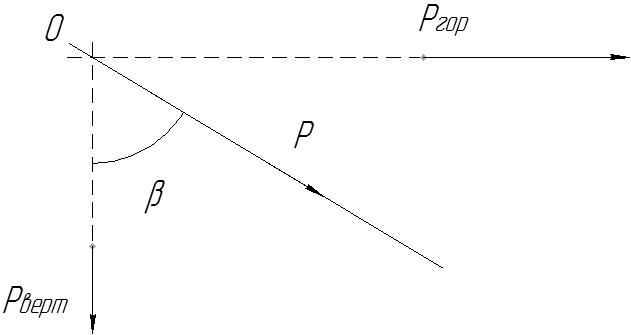 очка
0 , через которую проходит линия действия
P, находится на
пересечении линий действия
очка
0 , через которую проходит линия действия
P, находится на
пересечении линий действия
 .
Угол β находится из соотношения
(6.15).
.
Угол β находится из соотношения
(6.15).

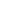

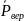
Рис. 6.3. Схема действия
векторов
Центр давления на плоской площадке
α
0



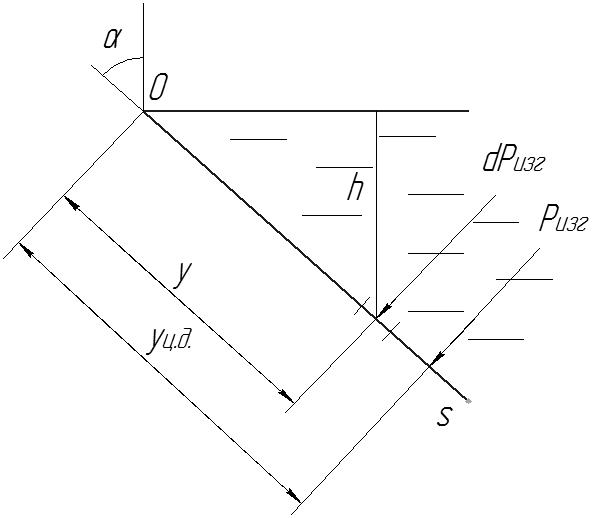 оордината
центра давления уц.д.
(рис. 6.4) определяется из соотношения
оордината
центра давления уц.д.
(рис. 6.4) определяется из соотношения
h



 (6.16)
(6.16)
y
yцд
(6.17)


S

Получаем
(6.18)

где I0
– собственный момент инерции площадки
S
,
 – статический момент инерции площадки
S
,
– статический момент инерции площадки
S
,
 – центр тяжести площадки S.
– центр тяжести площадки S.
Задачи
№ 6.1 (71)
Определить силу Р полного давления на плоскую торцевую стенку горизонтальной цилиндрической цистерны диаметром D=2,2 м, если уровень бензина удельного веса γ=720 кГ/м3 в цистерне находится на расстоянии Н=2,4 м от дна.
Цистерна герметически закрыта, и избыточное давление паров бензина на свободную поверхность составляет hб=367 мм рт. ст.
Ответ: Р=22,5 т; hЦД=1,337 м.
№ 6.2 (86)
Определить силы, растягивающие
горизонтальную цистерну, заполненную
жидкостью удельного веса![]() кг/м3
по сечениям АА и BB, диаметр
цистерны D=5м, длина
l=10м.
кг/м3
по сечениям АА и BB, диаметр
цистерны D=5м, длина
l=10м.

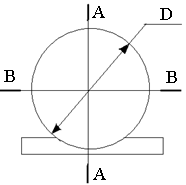
Рис. 6.5. Обозначение сечений в цистерне с жидкостью
Ответ:![]() т;
т;
![]() т.
т.
№ 6.3 (87)
Определить силу Р, действующую на болты шара D = 2м, заполненного водой.
D
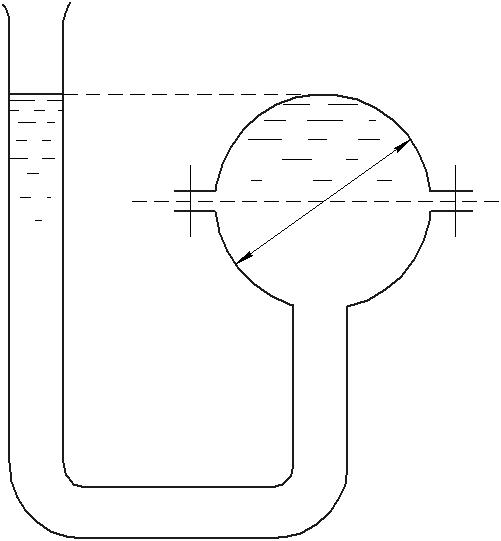
Рис. 6.6. Шар, наполненный водой
Ответ: =10,5 кН.
Задача № 6.4 (139)
Железнодорожная цистерна, заполненная
нефтепродуктом, удельного веса
![]() Движется со скоростью V=36км/час
по горизонтальному закруглению радиуса
R=300 м. Определить угол
наклона поверхности нефти.
Движется со скоростью V=36км/час
по горизонтальному закруглению радиуса
R=300 м. Определить угол
наклона поверхности нефти.
Ответ: tg = 0,034.
Задача № 6.5 (141)
Железнодорожная цистерна движется по
горизонтальному пути со скоростью
![]() .
Размеры цистерны:
.
Размеры цистерны:
![]() .
В некоторый момент времени поезд начинает
тормозить и на пути, равном
.
В некоторый момент времени поезд начинает
тормозить и на пути, равном
![]() ,
останавливается. Считая это движение
равномерно замедленным, определить
полное давление
,
останавливается. Считая это движение
равномерно замедленным, определить
полное давление
![]() жидкости на днище цилиндра, считая ее
удельный вес
жидкости на днище цилиндра, считая ее
удельный вес


Рис.1- Железнодорожная цистерна
Ответ:
![]()
Тема 7. Критерии подобия
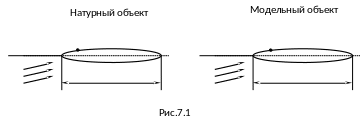
Первое определение подобия. Процессы
называются подобными на натурном объекте
(индекс «н») и модели (индекс «м»), если
в сходственных точках (А, 0,
![]() ,
,
![]() )
в сходственные моменты времени отношения
одноименных параметров
)
в сходственные моменты времени отношения
одноименных параметров
![]() на натурном объекте и модели (рис. 7.1)
одинаковы:
на натурном объекте и модели (рис. 7.1)
одинаковы:

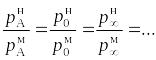 . (7.1)
. (7.1)
Аналогично для
![]() …
…
Второе определение подобия. Процессы называются подобными на натурном объекте и модели, если в сходственных точках в сходственные моменты времени на натурном объекте и модели одноименные безразмерные (индекс – *) параметры одинаковы:
![]() ,
,
![]() ,
…, (7.2)
,
…, (7.2)
где
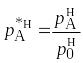 ,
,
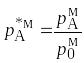 и так далее.
и так далее.
Основные критерии гидродинамического подобия могут быть получены из уравнения Навье – Стокса
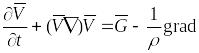
![]() .
.
в соответствии со вторым определением подобия.
Введем безразмерные параметры и обозначим
их (*). Тогда
![]() аналогично
аналогично
![]() ,
,
![]() и другие. Где индексом «0» обозначены
характерные (постоянные) параметры.
и другие. Где индексом «0» обозначены
характерные (постоянные) параметры.
Через безразмерные параметры запишется в виде
 .
.
После деления каждого слагаемого на
инерционный размерный комплекс
![]() получим
получим
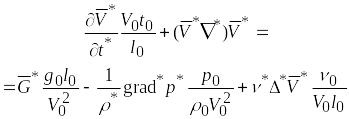 .
.
Безразмерные комплексы из характерных параметров являются критериями подобия:
1.
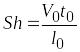 – число Струхаля, критерий подобия по
времени протекания процессов;
– число Струхаля, критерий подобия по
времени протекания процессов;
2.
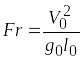 - число Фруда, критерий подобия по
действию массовых сил (поля тяжести);
- число Фруда, критерий подобия по
действию массовых сил (поля тяжести);
3.
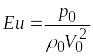 – число Эйлера, критерий подобия по
действию сил давления;
– число Эйлера, критерий подобия по
действию сил давления;
4.
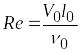 – число Рейнольдса, критерий подобия
по действию сил вязкости.
– число Рейнольдса, критерий подобия
по действию сил вязкости.
В соответствии с критериями подобия необходимо, чтобы, например, при подобии по действию сил трения (вязкости) выполнялись условия равенства чисел Re на натуре и модели:
![]() или
или
![]() ,
,
где
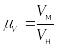 ,
,
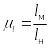 ,
– масштабы моделирования соответственно
по скорости, линейный и по вязкости.
,
– масштабы моделирования соответственно
по скорости, линейный и по вязкости.
Задачи
№ 7.1 (636)
Насос всасывает соляровое масло,
вязкостью υм=0,12 Cт
в количестве Qн=100
л/сек по трубе диаметром dн=200
мм. Из опытов с водой на этой модели
определяется минимальная (критическая)
глубина расположения конца всасывающей
трубы под свободной поверхностью
масла в резервуаре, при которой появляется
воронка и начинает засасывать воздух.
Определить диаметр dмконца
всасывающей трубы на этой модели,
количество всасываемой воды
![]() м
и критическую глубину Hкн
расположения конца всасывающей трубы
в натуре, если во время опытов на
модели было замечено, что воронка
прорывалась во всасывающую трубу
при критической глубине Hкм=
55 мм. Моделирование должно одновременно
производиться по Фруду и Рейнольдсу.
м
и критическую глубину Hкн
расположения конца всасывающей трубы
в натуре, если во время опытов на
модели было замечено, что воронка
прорывалась во всасывающую трубу
при критической глубине Hкм=
55 мм. Моделирование должно одновременно
производиться по Фруду и Рейнольдсу.
Ответ: dм=38,2 мм; м=1,6 л/сек; Hкн= 288мм.
№ 7.2 (639)
Модель самолета, изготовленная в 1/10 натуральной величины, испытывается на авторотацию в потоке воздуха и воды. Найти, во сколько раз увеличатся скорость и угловая скорость модели по сравнению со скоростью натуры, если соблюдается подобие сил вязкости. Также определить, на сколько сократиться при этом продолжительность времени происходящих в модели процессов.
Ответ: в воздухе VМ= 10VН, ωМ = 100ωН , tМ= 0,01tH; в воде υМ= 0,64υН, ωМ = 6,4ωН, tМ= 0,157tH .
Тема 8. Путевые потери напора Течение вязкой жидкости по трубам
До числа
 (критического) – течение устойчивое
ламинарное, после
режим меняется на турбулентный.
(критического) – течение устойчивое
ламинарное, после
режим меняется на турбулентный.
Напряжения трения на стенке трубопровода при ламинарном течении
(8.1)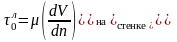 ,
,
при турбулентном
(8.2) .
.
При ламинарном установившемся
осесимметричном течении несжимаемой
жидкости вдоль оси
 (оси симметрии) трубопровода, пренебрегая
изменением давления поперек трубы, из
уравнения Навье – Стокса получим
(оси симметрии) трубопровода, пренебрегая
изменением давления поперек трубы, из
уравнения Навье – Стокса получим
(8.3) ,
,
где
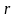 – произвольный радиус, на котором имеет
место скорость
– произвольный радиус, на котором имеет
место скорость
 (рис. 8.1). При
=0
скорость
(рис. 8.1). При
=0
скорость
 .
.
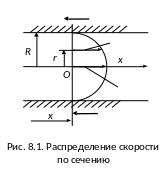
Интегрирование уравнения (8.3) для распределения скорости по сечению дает:
(8.4)
– параболический закон, а для потерь давления на участке длиной
(8.5)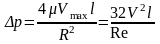
или
(8.6)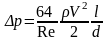 ,
,
где
 .
Расход жидкости через сечение
.
Расход жидкости через сечение
 трубы
трубы
(8.7)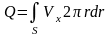 .
.
(8.8)
 ,
,
(8.9)
– коэффициент путевых потерь при ламинарном течении. Запись
(8.10)
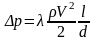
является общей для ламинарного и турбулентного течений. Число
(8.11)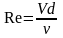 ,
,
где
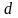 – диаметр трубопровода.
– диаметр трубопровода.
При турбулентном течении
(8.12) ,
,
где
 – отсчитывается от стенки трубы;
– отсчитывается от стенки трубы;
 – показатель, определяемый зависимостью
– показатель, определяемый зависимостью
 ,
(
,
( при
)
[4].
при
)
[4].
Связь между
 и
и
 определяется соотношением
определяется соотношением
(8.13)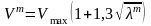 .
.
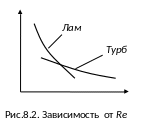 Коэффициент
потерь при турбулентном течении (при
Коэффициент
потерь при турбулентном течении (при
 )
)
(8.14)
–
формула Альтшуля, где
 – эквивалентная шероховатость
трубопровода, берется из справочников
по гидравлике. Подробности см. в [4, 1, 3].
– эквивалентная шероховатость
трубопровода, берется из справочников
по гидравлике. Подробности см. в [4, 1, 3].
Уравнение Бернулли с учетом потерь давления на трение
Для вязкой жидкости уравнение Бернулли имеет вид
(8.15) ,
,
где
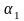 ,
,
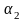 – коэффициенты кинетической энергии
(Кориолиса), учитывающие распределение
скорости по сечению (
)
трубы, определяются зависимостью
– коэффициенты кинетической энергии
(Кориолиса), учитывающие распределение
скорости по сечению (
)
трубы, определяются зависимостью
(8.16)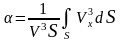 .
.
(8.17)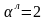 ,
для турбулентного
,
для турбулентного
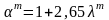 ,
,
(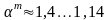 );
);
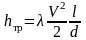 – потери напора на трение на участке
– потери напора на трение на участке
 ;
;
 – суммарные потери на местных
сопротивлениях,
– суммарные потери на местных
сопротивлениях,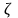 – коэффициент местных потерь.
– коэффициент местных потерь.
(8.18)
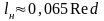 .
.
Коэффициент потерь напора на начальном участке
(8.19)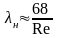 .
.
Задачи
№ 8.1 (307)
По прямой трубе длиной L= 1 км, диаметром d= 100 мм протекает жидкость со скоростью V= 0,4 м/с, имеющая кинематическую вязкость = 0,4 см2/с. Определить потерю напора на трение.
Ответ: hТР = 5,2 м.
№8.2 (323)
Определить потерю напора в трубе диаметром d = 270 мм и длинной L = =1000 м при Δэкв = 0,15 мм, если весовой расход нефти 200 т/ч, удельный вес γ = 0,88 т/м3, ν = 0,276 см2/с.
Ответ: hТР = 9 м.
№ 8.3 (344)
Труба имеет внезапное расширение от d1=100мм =0,1м до диаметра d2=300мм =0,3м. Определить потерю напора и коэффициент местных потерь напора, если объемный расход Q=35,3 л/с.
Ответ:![]() =64;
=64;
![]() =0,816м.
=0,816м.
Задача №8.4 (323)
Определить потерю напора в трубе диаметром d =270 мм и длинной L =1000 м при Δэкв =0,15 мм, если весовой расход нефти 200 т/ч, удельный вес γ = 0,88 т/м3, ν = 0,276 см2/с.
Ответ:hтр =9 м.
№8.5 (325)
Из резервуара по горизонтальной трубе
диаметром
![]() 50
мм, длиной
50
мм, длиной
![]() 20
м вытекает в атмосферу вода. Уровень
воды над осью трубы
20
м вытекает в атмосферу вода. Уровень
воды над осью трубы
![]() 4
м поддерживается постоянным. Определить
расход воды Q, пренебрегая
местным сопротивлением и принимая в
1-ом приближении λ=0,03.
4
м поддерживается постоянным. Определить
расход воды Q, пренебрегая
местным сопротивлением и принимая в
1-ом приближении λ=0,03.
Ответ:Q =5.02л/с.
№8.6 (326)
Решить задачу №8.5 (325) во втором и третьем
приближении, принимая
![]() и считая трубу абсолютно гладкой.
и считая трубу абсолютно гладкой.
Ответ:Q = 6,7 л/с.
№8.7 (342)
Решить задачу 325, принимая во внимание
местные потери напора при входе в трубу
![]() х
= 0,5 , в вентиле, установленном на конце
х
= 0,5 , в вентиле, установленном на конце
![]() = 3,5.
= 3,5.
Ответ:Q = 4,39 л/с.
Тема 9. Местные сопротивления. Истечения через отверстия и насадки
Внезапное расширение

На рис.а9.1 показано
течение при внезапном расширении при
больших
![]() .
.
Из уравнения Бернулли потерянный напор
при внезапном расширении при больших
на участке 1–2
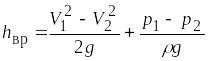 ,
а из уравнения импульсов имеем
,
а из уравнения импульсов имеем
![]() .
.
Тогда местные потери напора при внезапном расширении
(8.20)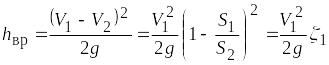 ,
,
где
![]() –
коэффициент местных потерь напора (по
отношению к
–
коэффициент местных потерь напора (по
отношению к
![]() ).
).
Или, если вычислять
![]() по формуле
по формуле
(9.1)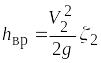 ,
,
то
(9.2)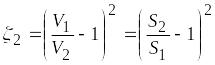 .
.
Истечение через диафрагму
На рис.9.2, показано истечение жидкости через диафрагму (отверстие в перегородке).

Потери на диафрагме
(9.3)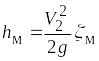 .
.
Коэффициент местных потерь на диафрагме
(9.4)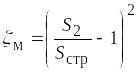 ,
,
где
![]() ,
а коэффициент поджатия струи определяется
зависимостью
,
а коэффициент поджатия струи определяется
зависимостью
(9.5) ,
,
где
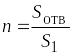 – степень сужения канала.
– степень сужения канала.
Истечения через отверстия и насадки при постоянном напоре
При истечении жидкости через отверстие на глубине H под свободной поверхностью (рис. 9.3) из уравнения Бернулли
(9.6) ,
,
где скорость идеальной жидкости
(9.7)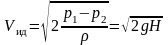 .
.

Из экспериментов коэффициент скорости
при истечении через “малое” отверстие
 ,
(
,
(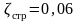 ).
).
(9.8)
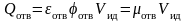 ,
,
(9.9)
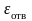 определяется по зависимости (8.25), а
степень сужения
определяется по зависимости (8.25), а
степень сужения
 для “малого” отверстия, т.е.
для “малого” отверстия, т.е.
 ,
и коэффициент расхода, следовательно,
,
и коэффициент расхода, следовательно,
 .
.
Таким образом, скорость при истечении
через отверстие почти не меняется по
сравнению с
 ,
а расход уменьшается примерно на 40%.
,
а расход уменьшается примерно на 40%.
При истечении через насадок (короткий
трубопровод рис. 9.4)
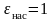 .
.

Из
формулы (9.4), рис. 9.2,
 ,
где внутреннее поджатие струи, как и
при истечении через отверстие
.
Тогда
,
где внутреннее поджатие струи, как и
при истечении через отверстие
.
Тогда
(9.10) ,
,
 .
.
Таким образом, скорость падает примерно на 20%, расход уменьшается также на 20% по сравнению с идеальным истечением.
Задачи:
№ 9.1 (520)
Водопроводе, находящимся под давлением
![]() ,
в результате сквозного проржавления
образовался свищ диаметром
,
в результате сквозного проржавления
образовался свищ диаметром
![]() .
Определить суточную утечку воды
.
Определить суточную утечку воды
![]()
Ответ:
![]() =16,1м3/сутки.
=16,1м3/сутки.
№ 9.2 (537)
Через цилиндрический насадок
длиною
![]() =25см
и диаметром d=5см,
приставленный с внешней стороны сосуда,
происходит истечение воды при постоянном
напоре H=3м.
Определить расход воды Q
( без учета и с учетом вязкости воды) и
максимальный вакуум hᵥ
, достигаемый
в пределах насадка.
=25см
и диаметром d=5см,
приставленный с внешней стороны сосуда,
происходит истечение воды при постоянном
напоре H=3м.
Определить расход воды Q
( без учета и с учетом вязкости воды) и
максимальный вакуум hᵥ
, достигаемый
в пределах насадка.
Ответ:
![]()
Тема 10. Нестационарные течения
10.1 Неустановившиеся течения
Уравнение Бернулли для неустановившегося течения жидкости в трубопроводе имеет дополнительное слагаемое
 , (10.1)
, (10.1)
при
 ,
уравнение Бернулли и имеет вид:
,
уравнение Бернулли и имеет вид:
 .
(10.2)
.
(10.2)
Задачи:
№ 10.1 (432)
Определить изменение скорости в начальной
стадии истечения идеальной жидкости
из трубы постоянного сечения, присоединенной
к резервуару, а также время
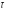 ,
по прошествии которого движение
становится стационарным.
,
по прошествии которого движение
становится стационарным.
Ответ:
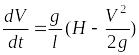 ;
;
![]() .
.
№ 10.2 (433)
Решить задачу № 10.1 (432), учитывая потери
на трение по длине и при входе в трубу.
Определить время
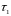 ,
по истечении которого скорость в трубе
достигнет 99% от величины скорости
стационарного течения
,
по истечении которого скорость в трубе
достигнет 99% от величины скорости
стационарного течения
 .
Определить объемный расход Q.
.
Определить объемный расход Q.
Ответ:
![]() .
.
№ 10.3 (434)
Идеальная жидкость колеблется в U - образной вертикальной трубке сечения d. Длина жидкости столба равна l. Определить период колебания.
Ответ:
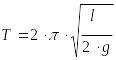 .
.
№ 10.4 (435)
Вода по штольне длиною
 м,
диаметром
м,
диаметром
 м.
поступает в уравнительную башню, имеющую
площадь поперечного сечения
м.
поступает в уравнительную башню, имеющую
площадь поперечного сечения
 .
Расход воды в штольне
.
Расход воды в штольне
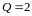 м3/сек
м3/сек
Ответ:
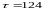 сек,
сек,
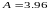 м.
м.
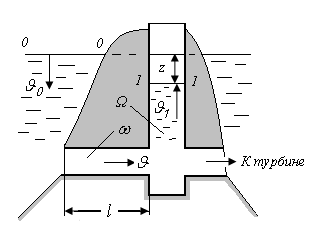
Рис. 10.1. Штольня
10.2. Гидравлический удар в трубах
Гидроудар возникает при внезапном перекрытии трубопровода. Он достигает максимального значения при “мгновенном” перекрытии и называется “прямым”. Приближенная модель расчета Н.Е. Жуковского строится на следующих положениях.
(10.3) в области торможения жидкости определяется
из уравнения изменения импульса
в области торможения жидкости определяется
из уравнения изменения импульса
 ,
,
где
 – затормозившаяся за время
– затормозившаяся за время
 масса, плотностью
масса, плотностью
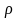 в области трубопровода, на длине
в области трубопровода, на длине
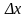 (с поперечным сечением
);
– скорость движения жидкости до
перекрытия трубопровода.
(с поперечным сечением
);
– скорость движения жидкости до
перекрытия трубопровода.
(10.4)
 обозначить скорость распространения
фронта остановившейся жидкости от
задвижки к открытому концу трубы (рис.
10.2),
обозначить скорость распространения
фронта остановившейся жидкости от
задвижки к открытому концу трубы (рис.
10.2),
 ,
то
,
то
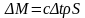 .
.
(10.5)

 .
.
2. Определим скорость
.
Скорость
зависит от сжимаемости жидкости
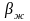 ,
определяющей изменение плотности (
,
определяющей изменение плотности ( ),
и от деформируемости трубопровода (
),
и от деформируемости трубопровода ( ,
,
 ),
определяющей изменение объема трубопровода
(
),
определяющей изменение объема трубопровода
(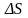 ).
).
Из закона сохранения массы в объеме
 ,
где
,
где
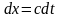 для приращения массы за время
для приращения массы за время
 имеем
имеем
(10.6)
или
(10.7) .
.
Определим относительное изменение
плотности
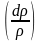 .
Так как относительное изменение объема
связано с коэффициентом сжимаемости
.
Так как относительное изменение объема
связано с коэффициентом сжимаемости
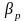 и модулем упругости жидкости
и модулем упругости жидкости
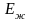 уравнением
уравнением
(10.8)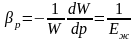 ,
,
то, учитывая, что
 ,
,
а для фиксированной массы
(10.9) ,
,
из (10.8) будем иметь
(10.10)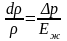 .
.
 Определим
относительное изменение поперечного
сечения трубопровода
Определим
относительное изменение поперечного
сечения трубопровода
 за счет повышения давления на
при гидроударе. Элемент трубопровода
представлен на рис. 10.3
за счет повышения давления на
при гидроударе. Элемент трубопровода
представлен на рис. 10.3
Относительное увеличение сечения
связано с относительным удлинением
окружности трубопровода (радиуса):
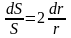 .
Относительное удлинение радиуса можно
определить из закона Гука
.
Относительное удлинение радиуса можно
определить из закона Гука
(10.11) ,
,
где – модуль линейной упругости (Юнга) материала трубопровода, а напряжение
(10.12) .
.
Тогда
(10.13) .
.
Подставляя в (10.7)
 из (10.10) и
из (10.10) и
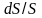 из (10.13), получаем
из (10.13), получаем
(10.14)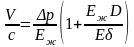 ,
,
а из совместного решения (10.5) и (10.14)
(10.15)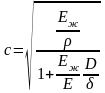 .
.
Таким образом, полученные уравнения (10.5) и (10.15) решают задачу повышения давления при гидроударе, когда время закрытия
(10.16) ,
,
где – длина трубопровода, и закрытие считается мгновенным.
В случае, если условие (10.16) не выполняется, то используется приближенная зависимость
(10.17)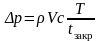 ,
,
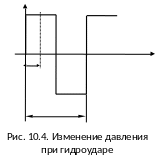
где
 (на рис. 10.4 показан характер изменения
давления при расчете гидроудара по
Н.Е. Жуковскому).
(на рис. 10.4 показан характер изменения
давления при расчете гидроудара по
Н.Е. Жуковскому).
Задачи:
№ 10.5 (422)
Определить объём воды V
, который следует накачать в трубопровод
диаметром
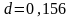 м,
длиной
м,
длиной
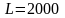 м,
если опрессовка трубопровода производится
водой при давлении
м,
если опрессовка трубопровода производится
водой при давлении
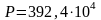 Па,
толщина стенок трубы
Па,
толщина стенок трубы
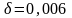 м,
материал- сталь:
м,
материал- сталь:
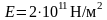 ,
,
 .
.
Ответ:

№ 10.6 (446)
По трубопроводу со средней скоростью
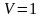 м/с перекачивается вода. Трубы стальные
с внутренним диаметром
м/с перекачивается вода. Трубы стальные
с внутренним диаметром
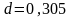 м;
толщина стенок
м;
толщина стенок
 м.
Определить по Жуковскому величину
ударного давления в трубопроводе
при мгновенном закрытии задвижки. Модуль
упругости стали
м.
Определить по Жуковскому величину
ударного давления в трубопроводе
при мгновенном закрытии задвижки. Модуль
упругости стали
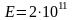 Н/м2, модуль объемного сжатия воды
Н/м2, модуль объемного сжатия воды
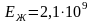 Н/м2.
Н/м2.
Ответ:
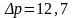 кг/см2.
кг/см2.
Часть 2. Решения задач Тема1. Аэродинамические силы и коэффициенты
Задача №1.1
Коэффициент запаса статической устойчивости ЛА
n=(ξdΣ− ξТ)/l. (1)

Из условия известны ξТ и l. Нужно найти суммарный коэффициент центра давления ξdΣ ЛА. В общем случае ξdΣ определим с помощью уравнения моментов сил, действующих на ЛА относительно носа аппарата (рис.1.1).
Аэродинамический момент относительно т.0 равен произведению суммарной силы на центр давления ЛА, т.е.
Мо= NΣξdΣ=Nкξdк+ Nцξdц, (2)
где NΣ= СNαк+цq∞Sмα; Nк= СNαкq∞Sмα; Nц= СNαцq∞Sмα; Sм=πd2/4.
Подставив в уравнение (2) значения сил, разделим его на СNαкq∞Sмα и получим:
ξdΣ=(СNαк ξdк+ СNαц ξdц)/ СNαк+ц (3)
В уравнении (3) неизвестными остаются ξdц и СNαц. Найдем их по формулам:
ξdц=lк+0,5lц,
СNαц= СNαк+ц−СNαк.
В соответствии с уравнением (2):
ξdΣ=(2·4/3+1·6)/3=2,9м.
Подставим полученное значение ξdΣ в (1):
n=(2,9−5,5)/10=−0,26.
Задача №1.2
Когда к ЛА добавится оперение в уравнении моментов относительно т.0 появится еще одно слагаемое (Nоп) NΣξdΣ= Nкξdк+ Nцξdц+ Nопξdоп,
где Nоп − сила, действующая на оперение.
NΣ= СNαΣq∞Sмα −сила, действующая на весь летательный аппарат.
Nк= СNαкq∞Sмα, Nц= СNαцq∞Sмα, Nоп= СNαопq∞Sопα –силы, действующие на изолированные элементы.
Для решения задачи не хватает параметра СNαΣ, который можно найти разделив уравнение NΣ= Nк+ Nц+ Nоп на q∞Sмα. Из этого получим:
СNαΣ = СNαк+ СNαопSоп / Sм+ СNαц.
Отсюда
(СNαкξdк+ СNαцξdц+ СNαопξdопSоп / Sм)/( СNαк+ СNαопSоп / Sм+ СNαц)=ξdΣ.
Подставим значения в получившееся уравнение и получим:
ξdΣ=(2·4/3+1·6+2·(10−0,5)·4/π)/(2+2·4/π+1).
ξdΣ=5,9.
n=(5,9−5,5)/10=0,04.
Задача №1.3
Для крылатого ЛА в качестве характерной площади принимается площадь крыльев в плане Sкр, включая подфюзеляжную часть.
Сила Nсам запишется:
Nсам= СNсамq∞Sкр,
где СNсам= СNαсамα;
СNα=∂СN/∂α при α=0.
Для самолета Nсам определится как сумма составляющих сил
Nсам= Nкр+ Nкорп+ Nопер, (1)
где Nкр, Nкорп, Nопер−силы, действующие на крылья, корпус, оперенье, которые можно найти по формулам:
Nопер= СNαоперq∞Sоперα;
Nкр= СNαкрq∞Sкрα;
Nкорп= СNαкорпq∞Sкорпα,
где, Sкр= S'корп+ S'кр; S'корп=d·b;S'кр=2·a·b; Sм= Sкорп=πd2/4.
Подставим эти данные в уравнение (1) и сократим на q∞Sкрα. Получим
СNαЛА = СNαкрS'кр/ Sкр+ СNαкорпSкорп/ Sкр + СNαоперS'опер / Sкр,
где S'опер=2Sопер.
В результате получим:
СNαЛА=2*6/7+2*0,785/7+2*1/7=2,22.
Положение центра давления определим из уравнения моментов относительно носка ЛА
NсамXdсам= NкрХdкр +NкорпХdкорп +NоперХdопер (2)
Уравнение (2) разделим на q∞Sкр:
СNαсам Xdсам= СNαкрХкрS'кр/ Sкр+СNαкорпХкорпSкорп/ Sкр + СNαоперХоперS'опер / Sкр
2,22 Xdсам=2*3,5*6/7+2*3,5*0,785/7+2*3,5*1/7
Xdсам=3,96м
 Xdсам=
Xdсам
/l=0,57
Xdсам=
Xdсам
/l=0,57
Задача №1.4
N2
N1



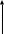
g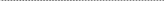






xd1
xT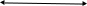


xd2
lк.о
l1




l2
Рис.1.2.Расчетная аэродинамическая схема
Коэффициент запаса статической устойчивости ЛА:
n=(xd2−хT)/ l2. (1)
В первом случае (имеем коническое тело с заданной массой) аэродинамический момент относительно центра тяжести направлен в сторону увеличения угла атаки (n<0), что приведет к потере устойчивости.
Чтобы увеличить запас статической устойчивости, к телу присоединяют невесомую коническую обячейку. Центр тяжести остается на прежнем месте, а центр давления смещается ближе к донной части.
Для конической поверхности центр давления находится на 2/3 длины от носа.
Тогда xd2=2/3 l2, где l2= l1+ lк.о., хT=3/4l1.
Подставив эти данные в выражение (1), получим:
n=(2/3 l1+2/3 lк.о.− 3/4 l1)/(l1+lк.о)
Выразим из этого уравнения lк.о:
lк.о. .=(1/12+n) l1/(2/3−n)
Подставим значение в уравнение и получим:
lк.о. .=0.45м.
Задача №1.5
Для бескрылого ЛА в качестве характерной площади принимают площадь поперечного сечения корпуса − площадь миделя.
Сила лобового сопротивления ракеты XЛА= СхЛАq∞Sм.
В данном случае будем считать, что на ракету действуют составляющие сил от давления. Составляющих сил от трения нет. Тогда Хр= Хркорп+ Хрдон,
где Хркорпи Хрдон− силы сопротивления от действия распределенного давления, действующие на изолированные элементы.
Xр= Сх ЛАq∞SмХркорп = Схкорпq∞SмХрдон = Схдонq∞S'дон,
где S'дон-площадь донного среза, создающего сопротивление (рис.1.3).
Сх ЛАq∞Sм= Схкорпq∞Sм+ Схдонq∞S'дон
СхЛА= Схкорп+ СхдонS'дон/ Sм

Рис. 1.3. Площадь донного среза
В первом случае S'дон =Sдон, так как двигатель не работает; во втором случае S'дон= Sдон-Sсопл, двигатель работает; в области сопла сопротивление не создается.
СхЛА=0,3+0,15*(0,5-0,3)/0,7=0,34.
Задача №1.6

Рис.1.4. Обтекаемое тело
Сила давления ветра
X=q∞SCx,
где S–характерная площадь. S=DH.
q∞–скоростной
напор набегающего потока воздуха.
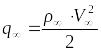 ,
,
∞–плотность воздуха. Из уравнения Менделеева–Клапейрона
![]() .
.
Для воздуха
![]() .
.
Выражая силу давления ветра, получим
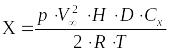 ,
,
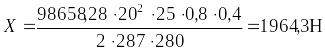 =200,4кг.
=200,4кг.
Задача №1.7
Давление ветра P на
пластину указателя скорости, площадью
![]() :
:
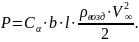
Вес пластины:

Уравнение равновесия пластины:
![]() .
.
Подставим сюда значения P,G,X. После сокращения получим:
Задача №1.8
В соответствии с рис.1.5 для решения данной задачи воспользуемся формулой
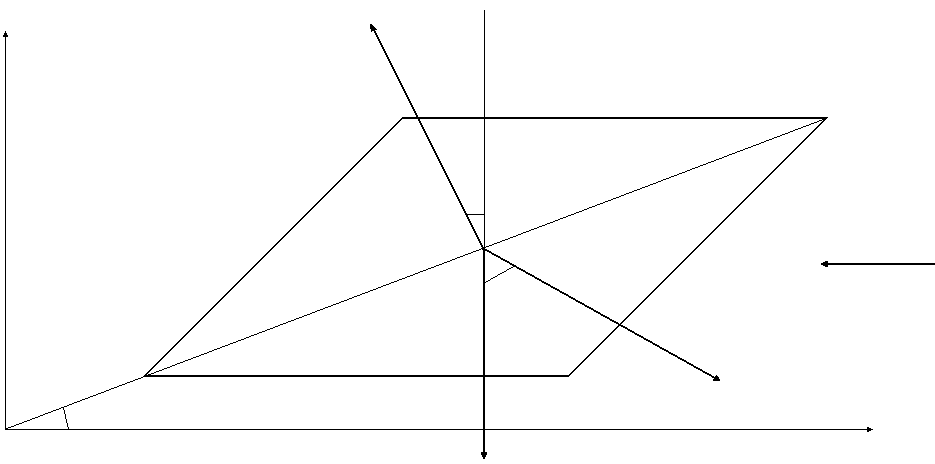
![]()
![]()
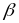
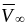
![]()
![]()
Ох
Рис.1.6.Схема приложения сил (перенести в часть первую)
![]() ,
,
где
![]() м
м![]() – площадь воздушного змея,
– площадь воздушного змея,
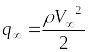 – скоростной напор,
– скоростной напор,
![]() – плотность воздуха, где p=
– плотность воздуха, где p=![]() –атмосферное
давление,
–атмосферное
давление,
![]() кг/м
кг/м![]() -плотность
ртути при
-плотность
ртути при
![]() [1],
[1],
![]() - изменение плотности от температуры,
- изменение плотности от температуры,
![]() кг/м
.
p=
кг/м
.
p=![]() =102992,2
Па.
=102992,2
Па.
![]() кг/м
кг/м
![]() Дж/кг К
– газовая постоянная воздуха.
Дж/кг К
– газовая постоянная воздуха.
Скоростной напор
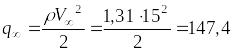 Па,
Па,
![]() =24,7
Па.
=24,7
Па.
Составим проекции действующих сил на оси
![]() (1)
(1)
![]() (2)
(2)
Подставим значения в (1) и (2):
K![]() Па, (3)
Па, (3)
K![]() Па. (4)
Па. (4)
Разделив (4) на (3), получим
![]() .
.
Угол между направлением нити и вертикалью
![]() .
.
![]() .
.
Сила натяжения нити:
K![]() =22,3Н=2,28кг.
=22,3Н=2,28кг.
(Ответ:
![]() ,K=2,28кг.
В результате решения задачи, полученные
значения, равны значениям в условии
задачи )
,K=2,28кг.
В результате решения задачи, полученные
значения, равны значениям в условии
задачи )
Задача №1.9
Cкорость движения тела можно заменить скоростью набегающего потока V=V.
Сила лобового сопротивления
X=q∞SмCx,
где q∞–скоростной напор набегающего потока воздуха.
,
∞–плотность воды. Примем
![]() .
.
Выражая силу давления воды, получим
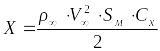 ,
,
![]() =114,8кг.
=114,8кг.
Мощность данной силы найдем через выражение
![]() ,
,
![]() =23л.с.
=23л.с.
Задача №1.10
Скорость парашютиста равна скорости набегающего потока V=V∞.
Поскольку скорость спуска парашютиста равномерная, то из второго закона Ньютона:
X=G.
Подъемная сила
X=q∞SCx,
где S–характерная площадь.
![]() .
.
q∞–скоростной напор набегающего потока воздуха.
,
∞–плотность воздуха. Из уравнения Менделеева–Клапейрона
.
Для воздуха .
Собирая все формулы воедино и выражая скорость набегающего потока, получим
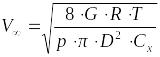 ,
,
 .
.
Задача №1.11
Скорость спускающегося груза равна скорости набегающего потока V=V∞. (рис.1.5)
Поскольку скорость спуска груза равномерная, то из второго закона Ньютона:
X=Q.
Рис. 1.8 Падающий груз
Подъемная сила найдется как
X=q∞SCx,
где S–характерная площадь. Найдется как
![]() .
.
q∞–скоростной напор набегающего потока воздуха. Найдется как
,
где ∞–плотность воздуха. Найдется из уравнения Менделеева–Клапейрона
.
Для воздуха .
Собирая все формулы воедино и выражая вес груза, получим
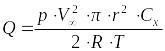 ,
,
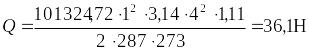 =3,68кг.
=3,68кг.
Тема 2. Уравнения неразрывности, импульса, Бернулли
Задача №2.1
В качестве важных сечений обозначим сечения 1, 2, 3.
За нулевой уровень примем сечение 1.
Для определения расхода воды и давления у нижнего основания воспользуемся уравнением Бернулли для несжимаемой жидкости выраженное в высотах.
V2/2g + y + P/(ρg) = C
VS = const – уравнение неразрывности.
Запишем итоговое уравнение для 3-х, важных сечений.
V12/2g + y1 + P1/(ρg) = V22/2g + y2 + P2/(ρg) = V32/2g + y3 + P3/(ρg);
(1) (2) (3)
где V1, V2, V3 – соответственно скорости в первом, втором и третьем сечениях.
P1, P2, P3 – соответственно давления в первом, втором и третьем сечениях.
y1, y2, y3 – высоты важных сечений, относительно нулевого уровня.
ρ – плотность жидкости.
g – ускорение свободного падения.
Из условия задачи: y1 = 0, P2 = P3 = Pатм, y2 = h, y3 = H+h, V3 = 0.
Объединяя (2) и (3) найдем V2:
V22/2g + y1 + P2/(ρg) = V32/2g + y3 + P3/(ρg),
подставим значения:
V22/2∙9,8 + 0,5 + 105/(1000∙9,8) = 0 + (8+0,5) + 105/(1000∙9,8), откуда
V2= 12, 52 м/с.
Найдём Q из выражения Q = V2S2:
Q = 12,52 (0,012π)/4 = 9,8∙10-4 м3/с = 0,98 л/с.
Теперь найдем V1:
V1 = V2S2/S1,
подставим значения:
V1 = 12,52 ((0,012π)/4) /((0,052π)/4) = 0,5 м/с.
Объединяя (1) и (2) найдем P1:
V12/2g + y1 + P1/(ρg) = V22/2g + y2 + P2/(ρg),
подставим значения:
0,52/2∙9,8 + 0 + P1/(1000∙9,8) = 12,522/2∙9,8 + 0,5 + 105/(1000∙9,8)
Откуда P1 = 83000 Па ≈ 0,83 атм.
Задача №2.2
Разность давлений между входным сечением и выходным:
∆p=p1– p2 ,
где: p1 - давление во входном сечении;p2 - давление в выходном сечении.
Запишем уравнение Бернулли:
![]() V12
/2 + g
V12
/2 + g![]() y1
+ p1/ρ=
V22
/2 + g
y2
+p2/ ρ,
y1
+ p1/ρ=
V22
/2 + g
y2
+p2/ ρ,
где: y1=0 т.к. нулевое положение находится на месте интересующего нас сечения;
y2=δ/2=0,1/2=0,05 м;
V1 - скорость потока во входном сечении;
V2 - скорость потока в выходном сечении;
Из уравнения неразрывности V1 S1=Q выразим V1:
V1 = Q/ S1,
где:
S1 = (π d 2)/4 = (3,14 0,04)/4 = 0,0314;
S1 - площадь первого сечения.
Для определения скорости V2 воспользуемся равенством:
V2 S2=V1 S1,
V2 = (V1 S1)/S2,
где:
S2 = π D δ = 3,14 1 0,1 = 0.314,
S2- площадь второго сечения.
Подставляем найденные значения в уравнение неразрывности:
V1 = 0,3 / 0,0314 = 9,6 м/с;
V2 = (9,6 0,0314)/0,314 = 0,96 м/с
Выражая значение Δp/ γ = (p1–p2)/ γ , из уравнения Бернулли, получим:
Δp/ γ = (p1–p2)/ γ = (V22 –V12)/2 g + δ/2 = (0,962 –9,62)/2 9,81 + 0,1/2 =
=–4,6 м
Задача №2.3
Запишем уравнение Бернулли для сечений 1 и 2:
V12 /2 + g y1 + P1/ ρ = V22 /2 + g y2 + P2/ ρ,
где: V1 - скорость потока в 1 сечении; V2 - скорость потока во 2 сечении.
y1 = δ/2 =0.1/2= 0.05.
Выражаем ΔP/ γ из уравнение Бернулли:
ΔP/ γ = (P1–P2)/ γ = (V22 –V12)/2 g + δ/2;
V2 = ω R = ω D/2 = 10 π D/2 = 10 3.14 1/2 = 15.7 м/с.
Из решения № 2 (167) задачи V1 = 9.55 м/с
ΔP/ γ = ((15,7) 2 – (9,55) 2)/2 9,8+ 0.1/2 = 8 м.
Запишем уравнение Бернулли с учётом вращательного движения и действия центробежного ускорения:
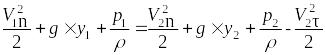 ,
,
где: V1n – скорость втекающей жидкости по нормали к сечению 1; V2n – скорость истекающей жидкости по нормали к сечению 2; V2τ – скорость истекающей жидкости по касательной к сечению 2; y1=0 – координата первого сечения; p1 – давление в первом сечении (на входе); p2=pатм=1 атм – давление во втором сечении (на выходе);
g∙y2= g∙δ/2
Рассчитаем Δp при
условии, что: V2τ![]() ,
V1n=0,
V2n=0;
,
V1n=0,
V2n=0;
тогда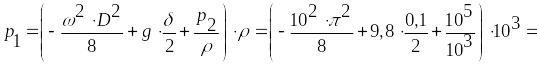 =
–0,23 атм.
=
–0,23 атм.
![]() атм,
атм,
или
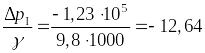 м.
м.
Рассчитаем величину
![]() при условии, что в нижнее отверстие
поступает жидкость с расходом Q=0,3
м3/с. Тогда скорость на входе будет
равна:
при условии, что в нижнее отверстие
поступает жидкость с расходом Q=0,3
м3/с. Тогда скорость на входе будет
равна:
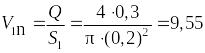 м/с
м/с
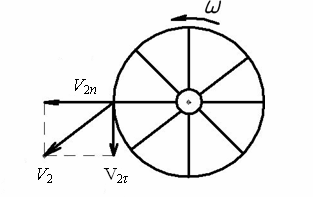
Рис. 2.1. Схема скоростей
Найдём скорость истекающей жидкости по нормали к сечению:
V2n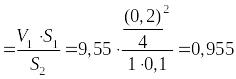 м/с
м/с
Подставляя данные в уравнение Бернулли находим:
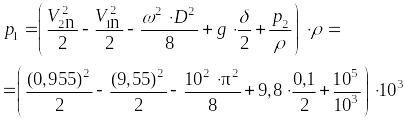 ,
,
![]() атм.
атм.
![]() =
=![]() атм
атм
или
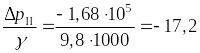 м
м
Задача №2.4
Уравнение установившегося движения для трубки тока:
m (V2 – V1) = R + G – (n1 p1 S1 + n2 p2 S2);
Рассмотрим закон сохранения импульса в случае с брандспойтом: давления внутри системы уравновешивают друг друга, следовательно закон сохранения импульса примет вид:
R = m V1;
S1 = (π d 2)/4,
где: R - сила, с которой пожарному приходиться удерживать брандспойт; V1, V2 - соответственно скорости в первом, втором сечении; m - массовый секундный расход; S1,2- площадь сечений; ρ- плотность воды.
Уравнение неразрывности:
m = ρ V1 S1;
При подстановке получаем:
R = ρ V12 S1 = 1000 (15)2 (3.14 (0.02)2)/4 = 70,65H=7,065 кг.
Задача №2.5
Для выполнения решений предварительно найдем скорости в сечениях S1 и S2.
Скорость потока в 1 сечении V1 = Q/S1;
скорость потока во 2 сечении V2 = Q/S2.
Из уравнения Бернулли
V12 /2 + g y1 + P1/ ρ = V22 /2 + g y2 + P2/ ρ;
y1=y2=0,
Выразим давление во втором сечении:
P2 = (ρ (V12 – V22))/2+P1;
P2 = 1.61 105 Па.
Найдем статические реакции:
RCТ=RCТ1+RCТ2 = ρ1 S1+ ρ2 S2;
RСТ1=895 Н, RСТ2=316 Н, RСТ=1211 Н= 123,5 кг.
Точка C, приложения RCТ, определяется из условия:
момент равнодействующей RCТ относительно точки А равен сумме моментов, составляющих RCТ1 и RCТ2.
AC RCT= AC1 RCT1+ AC2 RCT2.
Здесь AC1= d1/2; AC 2=d1/2+2R;
AC=51,9мм.
Динамическая реакция потока определяется:
RД = RД1 + RД2,
где: RД1,RД2 - соответственно, динамические реакции в первом и во втором сечениях;
RД1=ρ Q V1=ρ Q (Q/S1)=(ρ Q2)/S1=(1000 (20 10-3) 2 4)/3.14 (0.075) 2=
=90,6 H;
RД2=ρ Q V2=ρ Q (Q/S2)=(ρ Q2)/S2=(1000 (20 10-3) 2 4)/3.14 (0.05) 2 =
=203,8 H;
Суммарная реакция:
RД=294,4 H=30,01кг
Точка D, приложения силы RД, определяется из условия: момент равнодействующей RД равен сумме моментов, составляющих RД1 и RД2 относительно точки А.
AD RД=AD1 RД1+ AD2 RД2, где AD1= d1/2; AD2=d1/2+2R;
AD=138,5 мм.
Тема 3. Изэнтропические течения
Задача №3.1
Для решения данной задачи воспользуемся уравнением сохранения энергии
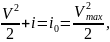
где V– скорость воздуха
при сжижении,i –
энтальпия![]() ,
,
![]() –
энтальпия газа в заторможенном состоянии
–
энтальпия газа в заторможенном состоянии
![]() ,
,![]() –
теплоемкость воздуха при постоянном
давлении.
–
теплоемкость воздуха при постоянном
давлении.
![]() 1000
1000![]() .
.
Отсюда скорость:
![]() 648,07
648,07![]()
Задача №3.2
Для решения задачи воспользуемся четвертой формой уравнения энергии
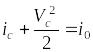 (1)
(1)
где
![]() - энтальпия газа на срезе сопла;
- энтальпия газа на срезе сопла;
![]() -
скорость движения газов на срезе сопла;
-
скорость движения газов на срезе сопла;
![]() - энтальпия в баллоне.
- энтальпия в баллоне.
Подставив выражения энтальпии в уравнение энергии, получим:
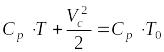 (2)
(2)
Выразим
![]() из уравнения (2)
из уравнения (2)
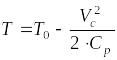 (3)
(3)
Для нахождения (температуры в баллоне) воспользуемся уравнением связи между давлением и температурой для изоэнтропических (идеальных адиабатических) процессов.
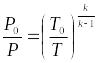 (4)
(4)
Подставим (3) уравнение в (4). Получим:
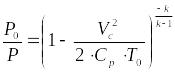 (5)
(5)
Выразим Т0 из уравнения (5):
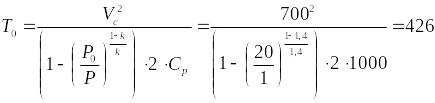 °
К
°
К
Задача №3.3
Для решения используем уравнение энергии для газа:
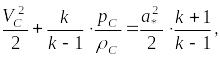 (1)
(1)
из которого выражаем скорость на срезе сопла:
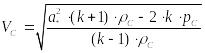 (2)
(2)
Квадрат скорости звука находим по формуле:
![]() (3)
(3)
Используя соотношение между критическими параметрами и параметрами полного торможения, запишем для температур:
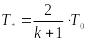 (4)
(4)
Запишем уравнение газового состояния для области полного торможения:
![]() (5)
(5)
Запишем соотношение для изэнтропического процесса:
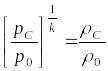 (6)
(6)
Подставляя
![]() из формулы (4) в формулу (3), получим:
из формулы (4) в формулу (3), получим:
![]() (7)
(7)
Выразив
![]() из уравнения (5), подставим его в уравнение
(6), разрешим уравнение (6) относительно
из уравнения (5), подставим его в уравнение
(6), разрешим уравнение (6) относительно
![]() :
:
 (8)
(8)
Подставляя (7) и (8) в 2, получим формулу для определения скорости истечения газов на срезе сопла:
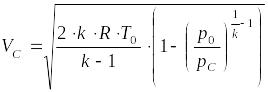 (9)
(9)
С учётом того что pС = 1 атм или ≈100000 Па, имеем:
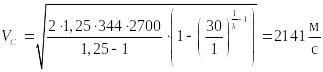
Сила тяги струи определится по формуле:
![]()
![]() (10)
(10)
Из формулы (10) находим:
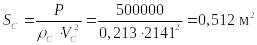 ,
(11)
,
(11)
массовый секундный расход
![]() . (12)
. (12)
Разрешим формулу (12) относительно площади для критического сечения:
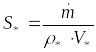 ,
(13)
,
(13)
По формуле (4) находим температуру в критическом сечении:
![]()
По формуле (3) найдём скорость истечения газов в критическом сечении:
![]() .
.
Выражение для плотности газа в критическом сечении:
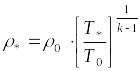 .
(14)
.
(14)
Подставляя
 из формулы (5), и температуру из формулы
(4), получаем:
из формулы (5), и температуру из формулы
(4), получаем:
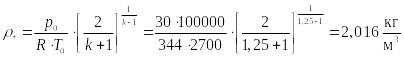 .
.
Тогда площадь критического сечения будет равна:
![]() .
.
Найдём удельную тягу:
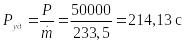 .
.
Геометрические характеристики сопла:
диаметр сопла:
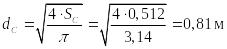 ,
,
диаметр критического сечения:
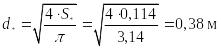 ,
,
длина сопла:
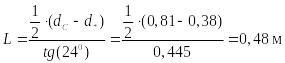 .
.
Задача №3.4
Для решения задачи воспользуемся уравнением энергии
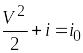 , (1)
, (1)
гдеV- скорость потока, i – энтальпия и находится по формулам
![]() , (2)
, (2)
![]() . (3)
. (3)
Параметры стратосферы: Т=216,6,
![]() =1000
Дж/кг∙К [2].
=1000
Дж/кг∙К [2].
Подставляя выражения (2) и (3) в формулу (1) получаем:
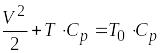 . (4)
. (4)
Выразим
![]() из формулы (4):
из формулы (4):
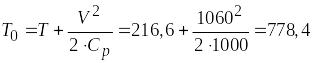 К.
К.
Тема 4.Скачки уплотнения
Задача №4.1
Запишем выражение для скорости тела через число Маха и скорость звука:
V=Ma=a/sin(μ), (1)
где V – скорость тела (самолета), а=346 м/с – скорость звука в воздухе, μ – угол полураствора конуса Маха.
Скорость самолета
V=BD/t (2)
BD=H/tg(μ), (3)
где Н – высота полета. Откуда
V=H/(tg(μ)*t) (4)
Составляем уравнение
a/sin(μ)=H/(tg(μ)*t), (5)
откуда находим:
μ=arccos (ta/H)=arccos (2,15∙346/1000)=0,732=420 , (6)
Подставляя μ в выражение (4), находим V:
V=H/(tg (μ)t)=1000/(tg(420)2,15)=518 м/с.
Задача №4.2
Зная угол между скачком уплотнения и
поверхностью иглы, определим число Маха
(![]() ).
Примем
).
Примем
![]()
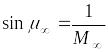 ,
,
отсюда
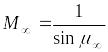
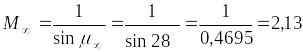 .
.
Определим температуру набегающего
потока (![]() ).
Отношение температуры торможения к
температуре набегающего потока через
число Маха выражается следующим образом
).
Отношение температуры торможения к
температуре набегающего потока через
число Маха выражается следующим образом
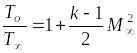 ,
,
где k=1,4.
Отсюда температура набегающего потока равна
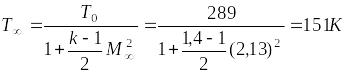 .
.
Зная
![]() ,
определим скорость звука (
,
определим скорость звука (![]() )
)
![]() ,
,
где R-газовая постоянная
![]() .
.
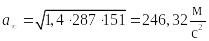 .
.
Найдем скорость набегающего потока
![]()
Задача №4.3
Справочные величины:k=1,4 ;R=287Дж/кг·К.
Для нахождения скорости воздуха после скачка воспользуемся соотношениями для связи параметров торможения с критическими параметрами:
![]()
где V1 – скорость
потока до скачка; V2
– скорость потока после скачка;
![]() – критическая скорость звука.
– критическая скорость звука.
Вторым связующим соотношение используем выражение для постоянных теплоемкостей:
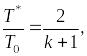
где T0 – температура в форкамере, Т* – в критическом сечении.
Выражаем и находим Т* :
![]()
![]()
ЗнаяТ*, используя известную
зависимость, найдем
![]() :
:
![]()
![]()
Подставим найденное и найдем V2 :
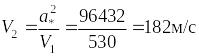 .
.
Задача №4.4
Справочные величины:k=1,4;Ср=287 Дж/кг·К.
Температура, которую показывает термопара, является температурой полного торможения.
Запишем уравнение энергии:
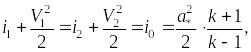
где i1 и i2 – энтальпия до и после скачка уплотнения; i0 – энтальпия торможения; V1 и V2 – скорости потока до и после скачка уплотнения; – критическая скорость звука; k – адиабатическая постоянная газа.
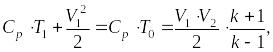
где Ср – удельная теплоемкость воздуха при р=const, Ср =1000 Дж/кг·К; k=1,4 для воздуха.
Из выражения найдем V1, а затем Т1 :
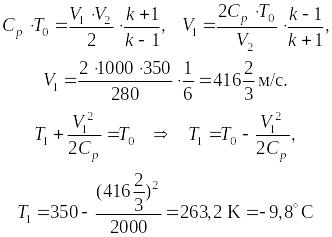
Задача №4.5
Коэффициент восстановления давления равен
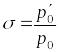 .
.
Воспользуемся формулой Релея:
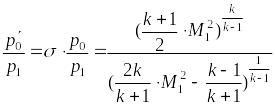 .
.
Отношение давления полного торможения потока, прошедшего скачок (измеренное трубкой полного напора), к давлению на верхней щеке клина (р1) равно 12, запишется:
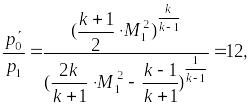
где М1 – число Маха в невозмущенном сверхзвуковом потоке; k = 1,4 – адиабатическая постоянная газа (в данном случае воздуха).
Подставим k в (3.2) и перепишем:
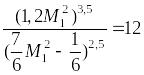
Путем подбора получим М1 = 3.
Отношение давления полного торможения, измеренного в сверхзвуковом потоке до скачка, к давлению невозмущенного потока:
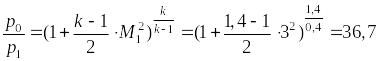
Выразим и найдем из выражения
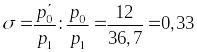 .
.
Задача № 4.6
Переведем скорость набегающего потока
из километров в час в метры в секунду:
![]()
Найдем значение числа Маха в невозмущенном потоке:
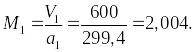
Используя найденное значение числа Маха (4.1), найдем давление полного торможения за скачком по формуле Релея:
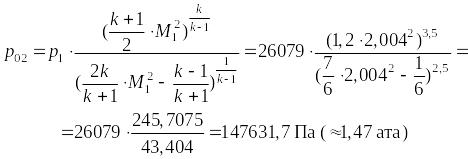
Давление полного изэнтропического торможения:
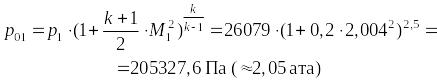
Задача №4.7
Для нахождения скорости полета воспользуемся следующей формулой:
 (1)
(1)
где
 - число Маха,
- число Маха,
 – скорость звука,
– скорость звука,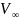 - скорость полета.
- скорость полета.
На высоте 15000м известны следующие значения: p=105,67 мм.рт.ст.=0,139ата , Т=216,5 К, a= 295м/с.
Для нахождения числа Маха воспользуемся формулой
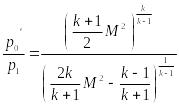 .
(2)
.
(2)
Соотношение (2) называют формулой Релея,
где![]() -
давление, определяемое трубкой полного
напора, p1 -
давление на высоте 15000м, к=1,4.
-
давление, определяемое трубкой полного
напора, p1 -
давление на высоте 15000м, к=1,4.
Для нахождения числа Маха воспользуемся
методом подбора, и определим с точностью
до четырех знаков
![]() =1,8944.
=1,8944.
Теперь воспользуемся формулой (1) и найдем скорость полета
![]()
Задача №4.8
Из
![]() ,
,
где ![]() ;
;![]() ;
;
![]() ;
;
![]() ,
,
можно выразить
![]() :
:

![]() .
.
Зная тангенциальную и нормальную скорости можно найти :
![]() .
.
Из выражения
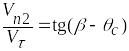 ,
,
следует
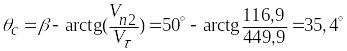 .
.
Задача №4.9
Для того чтобы геометрически найти
скорость потока за скачком, необходимо
построить план скоростей потока до
скачка и после скачка рис 4.6. Для этого
в определенном масштабе (в данной задаче
масштабный коэффициент
![]() )
откладываем вектор скорости
)
откладываем вектор скорости
![]() .
Длина этого вектора на рисунке равна
80мм. Раскладываем вектор
на нормальную
.
Длина этого вектора на рисунке равна
80мм. Раскладываем вектор
на нормальную
![]() и тангенциальную
и тангенциальную
![]() составляющие.
составляющие.
Под углом
![]() к вектору скорости невозмущенного
потока проводим прямую через точку O
(полюс плана скоростей). Пересечением
этой прямой с вектором
получаем точку A. Так как
к вектору скорости невозмущенного
потока проводим прямую через точку O
(полюс плана скоростей). Пересечением
этой прямой с вектором
получаем точку A. Так как
![]() (из теории косого скачка), то вектор
(из теории косого скачка), то вектор
![]() равен вектору скорости
равен вектору скорости
![]() потока за скачком.
потока за скачком.
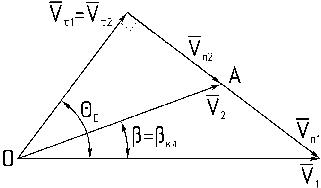
Рис.4.6. План скоростей
Измеряя и умножая длину этого вектора
на масштабный коэффициент
![]() ,
получим модуль вектора скорости потока
за скачком
,
получим модуль вектора скорости потока
за скачком
![]()
Для решения задачи аналитически, воспользуемся следующими соотношениями из теории о косом скачке, из рисунка
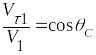
![]() ;
;
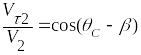
![]() ;
;
![]()
![]()
Тогда скорость потока за скачком равна
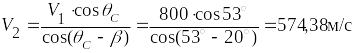
Тема 5.Обтекание тел
Задача № 5.1
В соответствии с условием (H=0) можно написать, что скорость звука а=340,28 м/с; плотность воздуха ρ=1,2 кг/м3; адиабатическая постоянная газа k=1,4; кинематическая вязкость ν=1,4607·10-5 м2/с.
Скоростной напор невозмущенного потока:
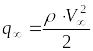 , (1)
, (1)
где
![]() –
скорость потока. В соответствии с этим
скоростной напор будет равняться:
–
скорость потока. В соответствии с этим
скоростной напор будет равняться:
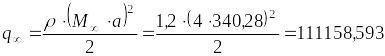 Па.
Па.
Для нахождения всех аэродинамических
коэффициентов используется коэффициент
давления торможения, который для![]() находится по следующей формуле:
находится по следующей формуле:
![]()
Найдем некоторые геометрические параметры конуса. Диаметр основания конуса найдем как:
![]() м,
м,
тогда площадь боковой поверхности будет равна:
![]() м2,
м2,
а площадь основания (площадь миделя):
![]() м2.
м2.
Найдем силу, действующую на боковую
поверхность
![]() ,
силу донного сопротивления
,
силу донного сопротивления
![]() и силу продольного сопротивления R
при α=0°.Для нахождения силы,
действующей на боковую поверхность,
воспользуемся формулой:
и силу продольного сопротивления R
при α=0°.Для нахождения силы,
действующей на боковую поверхность,
воспользуемся формулой:
![]() ,
,
где
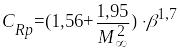 –
коэффициент продольной силы (от давления).
–
коэффициент продольной силы (от давления).
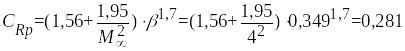 ,
,
тогда
![]() H
H
Найдем силу сопротивления корпуса от давления, действующего на донный срез:
![]() , (2)
, (2)
где
![]() –
коэффициент донного сопротивления:
–
коэффициент донного сопротивления:
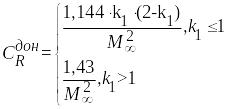 ,
,
где
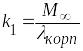 ,
,
![]() ,
тогда
,
тогда
![]() ,
,
соответственно,
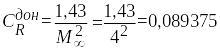 .
.
Используя формулу (2), получим:
![]() H.
H.
Силу продольного сопротивления находим по формуле
![]() ,
,
где
![]() –
коэффициент силы продольного сопротивления:
–
коэффициент силы продольного сопротивления:
![]() , (3)
, (3)
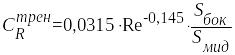 –
коэффициент трения,
–
коэффициент трения,
![]() –
число Рейнольдса.
–
число Рейнольдса.
![]()
В соответствии с этим коэффициент трения будет ровняться:
![]() (4)
(4)
Подставляя в уравнение (3) получим:
![]() ,
,
таким образом
![]() H
.
H
.
Найдем силу трения
![]() ,
коэффициент нормальной силы
,
коэффициент нормальной силы
![]() и нормальную силу
и нормальную силу
![]() ,
действующую на конус при
,
действующую на конус при![]()
Сила трения
![]() , (5)
, (5)
где, как указывалось раннее,
![]() –
коэффициент трения и т.к. он не зависит
от угла атаки (
),
то из (4) следует:
–
коэффициент трения и т.к. он не зависит
от угла атаки (
),
то из (4) следует:
![]() .
.
Используя формулу (5) получим:
![]() H.
H.
Найдем коэффициент нормальной силы:
![]() .
.
Подставляя данный коэффициент в формулу для расчета нормальной силы:
![]() ,
,
получим:
![]() H
H
Задача №5.2
Найдем коэффициент давления по формуле
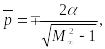
где
![]() – угол атаки,
– угол атаки,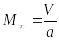 – число Маха, V –
скорость набегающего потока, a=340
м/с – скорость звука. Тогда
– число Маха, V –
скорость набегающего потока, a=340
м/с – скорость звука. Тогда
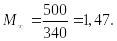
При![]() рад
рад
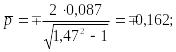
при![]() рад
рад
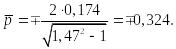
Найдём нормальные силы:
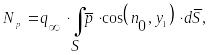
где
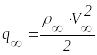 – скоростной напор невозмущённого
потока,
– скоростной напор невозмущённого
потока,
![]()
![]() –
плотность воздуха невозмущённого
потока. Тогда
–
плотность воздуха невозмущённого
потока. Тогда
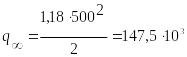 Па.
Па.
При![]() рад
рад
![]() Н;
Н;
при рад
![]() Н.
Н.
Найдем коэффициент нормальной силы по формуле
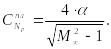
При рад
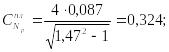
при рад
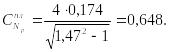
Найдём нормальные силы N по формуле:
![]() ,
,
где
![]() =S=
1
–
площадь пластины в плане.
=S=
1
–
площадь пластины в плане.
При![]() рад
рад
![]() Н;
Н;
при рад
![]() Н.
Н.
Определим коэффициент силы продольного сопротивления по формуле
![]() ,
,
где
![]() – коэффициенты для пластины.
– коэффициенты для пластины.
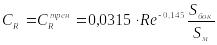 ,
,
где
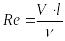 – число Рейнольдса,
– число Рейнольдса,
![]()
![]() –
кинематический коэффициент вязкости
потока,
–
кинематический коэффициент вязкости
потока,
![]() – площадь боковой поверхности пластины.
Тогда
– площадь боковой поверхности пластины.
Тогда
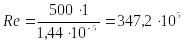 ,
,
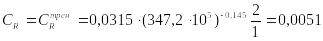
Задача №5.3
Найдем коэффициент давления для нижней поверхности
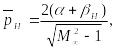
для верхней поверхности
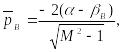
где
![]() рад,
рад,
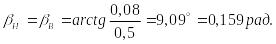 Тогда
при
Тогда
при
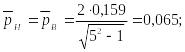
при
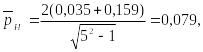
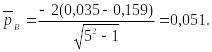
Найдем коэффициенты , для профиля ромба
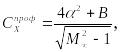
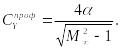
Где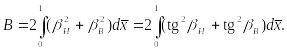 Тогда
Тогда
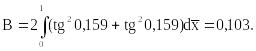
При
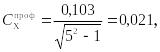
![]()
При
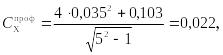

Задача №5.4
Найдем для сверхзвуковых скоростей
полета
![]() коэффициент силы продольного сопротивления:
коэффициент силы продольного сопротивления:
![]() ,
,
где
![]() – коэффициент трения ,
– коэффициент трения ,![]() – Коэффициент продольной силы,
– Коэффициент продольной силы,
![]() –
коэффициент силы донного сопротивления.
–
коэффициент силы донного сопротивления.
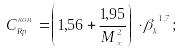
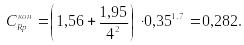
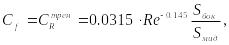
где
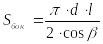 – боковая поверхность конуса,
– боковая поверхность конуса,
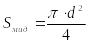 – площадь миделева сечения,
– площадь миделева сечения,
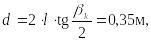
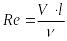 – число Рейнольдса,
– число Рейнольдса,
![]() – скорость набегающего потока,
– скорость набегающего потока,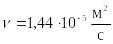 – кинематическая вязкость потока, a=340
м/с – скорость звука в набегающем потоке.
Тогда
– кинематическая вязкость потока, a=340
м/с – скорость звука в набегающем потоке.
Тогда
![]()
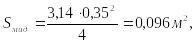
![]()
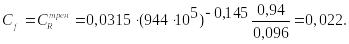
Для
сверхзвуковых скоростей полета (![]() )
)
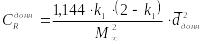 при
при
![]() ,
,
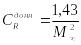 при
при
![]() ,
,
где
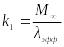 ;
;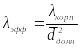 ;
;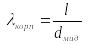 .
Тогда
.
Тогда
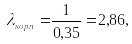
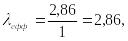
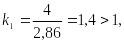
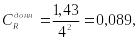
![]()
Находим
![]() по
ньютоновской теории по формуле
по
ньютоновской теории по формуле
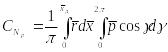 ,
,
где
![]() – коэффициент давления,
– коэффициент давления,
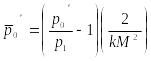
– коэффициент давления полного торможения газа,
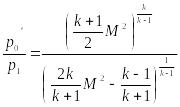 .
.
Коэффициент центра давления для конуса
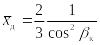 .
Тогда
.
Тогда
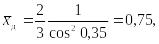
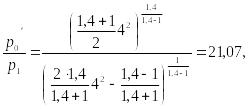
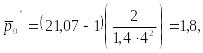
![]()
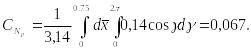
Тема 6. Гидростатика
Задача №6.1
Для полного давления на плоскую торцевую стенку воспользуемся следующей формулой
![]() ,
(1)
,
(1)
где
![]() (2)
(2)
– избыточное давление паров бензина.
![]() (3)
(3)
– давление столба бензина.
![]() - высота столба бензина над центром
тяжести;
- высота столба бензина над центром
тяжести;
![]() - площадь торцевой стенки.
- площадь торцевой стенки.
Подставив, уравнения (2), (3) в (1), получим:
![]() . (4)
. (4)
Найдём и :
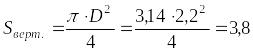 м2
(5)
м2
(5)
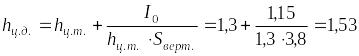 м,
(6)
м,
(6)
где
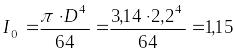 м4–
собственный момент инерции стенки.
м4–
собственный момент инерции стенки.
![]() м
– высота столба бензина над центром
тяжести стенки.
м
– высота столба бензина над центром
тяжести стенки.
Подставив полученные значения в формулу (6),получим:
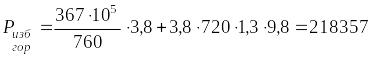 Н, или 21,8357 т.
Н, или 21,8357 т.
Задача № 6.2 (86)
Сечение ВВ (рис. 6.5.) растягивает вертикальная составляющая силы давления, которая равна
![]() ,
(1)
,
(1)
где
![]() –
давление на свободной поверхности,
–
давление на свободной поверхности,![]() – вертикальная проекция площадки S,
на которую действует сила давления,
– вертикальная проекция площадки S,
на которую действует сила давления,![]() - удельный вес жидкости, заполняющей
цистерну,
- удельный вес жидкости, заполняющей
цистерну,
![]() – объем тела давления.
– объем тела давления.
Давление Р0 на свободной поверхности уравновешивается внутренним давлением жидкости цистерны, следовательно
![]() ;
;
Объем тела давления:
![]() ,
(2)
,
(2)
где
![]() – объем параллелепипеда,
– объем параллелепипеда,![]() – объем цилиндра (цистерны)
– объем цилиндра (цистерны)
![]() м3,
м3,
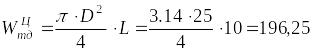 м3;
м3;
Тогда
![]() м3;
м3;
Теперь найдем
![]() :
:
![]() кг;
кг;
Аналогично сечение АА растягивает горизонтальная составляющая силы давления жидкости, которая равна
![]() ,
(3)
,
(3)
Как уже было сказано выше, Р0=0, тогда
![]() ,
,
где
![]() – координата центра тяжести цистерны,
которая равна половине диаметра, т.е.
2,5 м,
– координата центра тяжести цистерны,
которая равна половине диаметра, т.е.
2,5 м,![]() – вертикальная проекция .
– вертикальная проекция .
![]() м2;
м2;
Тогда
![]() кг;
кг;
Задача №6.3
Запишем выражение для вертикальной составляющей силы давления:
![]() ,
,
где![]() – избыточное давление,
– избыточное давление,
![]() – плотность воды при нормальных условиях,
– плотность воды при нормальных условиях,
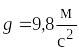 – ускорение свободного падения,
– ускорение свободного падения,
![]() – объем тела давления.
– объем тела давления.
Объем тела давления найдем по формуле:
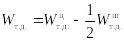 ,
,
где
![]() – объем цилиндра,
– объем цилиндра,
![]() – объем шара.
– объем шара.
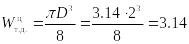 м3;
м3;
![]() м3.
м3.
Подставляя полученные значения, получим:
![]() м3.
м3.
Зная объем тела давления, найдем силу, действующую на болты:
![]() Н
.
Н
.
Задача №6.4
Для решения задачи воспользуемся геометрическими соображениями. Определив значения каждого из векторов, мы сможем найти угол между ними.
Определим инерционное ускорение
![]() :
:
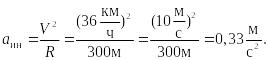
Найдем тангенс угла наклона:
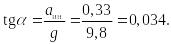
Задача №6.5
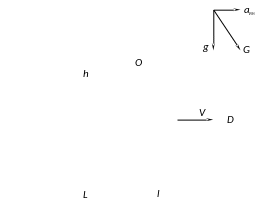

Рис.6.7. Система сил, действующих на цистерну.
Сила давления на площадку расположенной
под углом
![]() находится по формуле:
находится по формуле:
![]()
![]() ,
,
где
![]() – объем тела давления в направлении α.
– объем тела давления в направлении α.
Чтобы определить угол необходимо решить задачу кинематики, так как именно под углом к силе давления на днище цистерны направленно полное ускорение.
Уравнения кинематики:
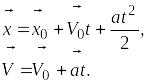
Спроецируем эти уравнения на ось x:
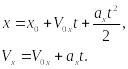
В этих уравнениях:
![]() .
.
После подстановки значений в уравнения примут вид:
![]()
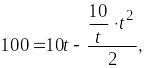
![]()
![]()
Так как формула используется при
рассмотрении системы в относительном
покое, то находится ускорение
![]() .
.
Полное ускорение находится как
![]()
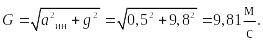
Определим угол , так как он необходим для нахождения объем тела давления :
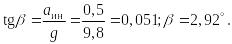
Найдем объем тела давления
![]() :
:
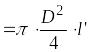 ,
,
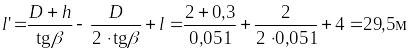 ,
,
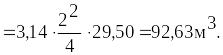
Определим силу давления на днище цистерны:
![]()
Тема 7. Критерии подобия
Задача №7.1
Для решения данной задачи сведем заданные и неизвестные геометрические характеристики к линейному масштабу:

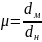 . (1)
. (1)
Запишем формулу для определения расхода жидкости для натуры и модели:
![]()
![]()
Перепишем формулу учитывая линейный масштаб:
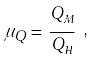
![]()
Итак запишем основные критерии гидродинамического подобия учитывая линейный масштаб через число Рейнольдса и Фрудо, соответственно:
По Рейнольдсу:
 =1.
=1.
По Фруду:
![]() ,
,
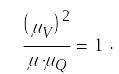
Определим линейный масштаб коэффициента вязкости:
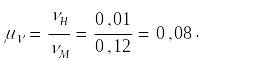
Так как в формуле записанной через число Фруда, можно записать следующее равенство:
![]() (2)
(2)
Подставив данное равенство (2) в формулу характеризующуюся через Re, получим:
![]()
![]()
![]()
Определив линейный масштаб из формулы (1) выразим dм и Нкн:
![]()
![]()


Для определения расхода жидкости необходимо подсчитать масштаб:
![]()
Количество всасываемой воды определится из формулы:
![]()
![]()
Задача №7.2
По условию:
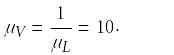
Тогда для угловой скорости:
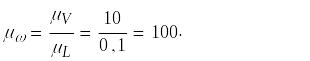
Определим продолжительность времени происходящих в модели процессов:
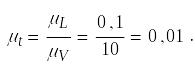
Следовательно, линейная и угловая скорости, продолжительность времени модели в потоке воздуха равны: VМ= 10VН, ωМ = 100ωН , tМ = 0,01tH.
Теперь обозначим коэффициент масштабирования для вязкости:

Вычислим также линейные и угловые скорости, продолжительность времени происходящих процессов для модели в потоке воды:
![]()
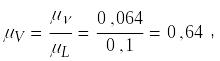
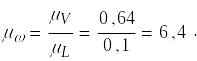
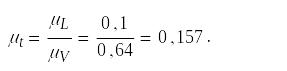
Следовательно, линейная и угловая скорости, продолжительность времени модели в потоке воды равны: VМ= 0,64VН, ωМ = 6,4ωН , tМ = 0,157tH .
Тема 8. Путевые и местные потери напора
Задача №8.1 (307)
Для решения поставленной задачи будем использовать уравнение Бернулли:
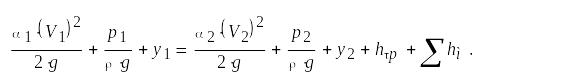
Так как труба прямая, то следовательно нет местных сопротивлений на трубе:
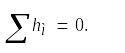
В данной задаче не сказано про начальную и конечную скорости (средняя скорость) и уровень трубы один и тот же, также не сказано про начальную и конечные давления, следовательно:
![]()
Отсюда:
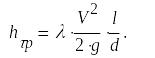 (1)
(1)
где коэффициент путевых потерь при ламинарном течении:
![]() (2)
(2)
где Re число Рейнольдса:
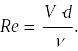 (3)
(3)

Задача №8.2 (323)
Определим площадь сечения трубы:
S=π·d2/4,
S=π·0,272/4=0,057 м2 ,
Найдём скорость течения:
V=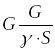 ,
,
V=−544/(8624·0,057) =1,107 м/с , Найдём число Рейнольдса для определения характера течения (ламинарный или турбулентный):
Re= V·d/ ν ,
Re=1,107·0,27/0,276·10−4=1,083·104 .
Re>Reкр – отсюда следует, что течение турбулентное.
Коэффициент потерь при турбулентном течении
λт=0,11·(68/Re+∆экв/d)0,25,
λт=0,11·(68/1,083·104+0,00015/0,27)0,25=0,032
Найдём потери напора на трение:
hтр=λт·(V2/2·g)·(L/d) ,
hтр=0,032·1,1072/2·9,8·1000/0,27=7,41 м,
Задача №8.3 (344)
Из уравнения Бернулли и уравнения импульсов имеем:
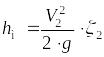 ,
(1)
,
(1)
где
–
коэффициент местных потерь напора (по
отношению к![]() ).
).
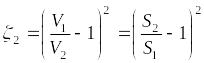 .
.
Определим площадь сечения трубы для диаметров d1 и d2:
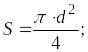
 ;
;
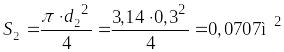 .
.
Найдём
скорость течения в сечении трубы
диаметраd2если
![]() ;
;
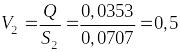 м/с.
м/с.
Определим – коэффициент местных потерь напора (по отношению к ) воспользовавшись формулой (2):
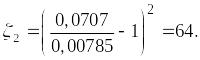
Найдем по формуле (1):
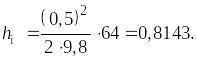
Задача №8.4 (323)
Определим площадь сечения трубы:
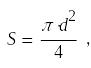
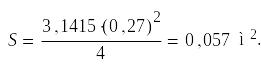
Найдём скорость течения:
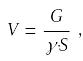
где G= 0,055 т/с , γ = 0,88 т/м3, S = 0,057 м2.
Отсюда:
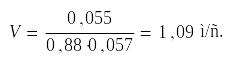
Найдём число Рейнольдса для определения характера течения (ламинарный или турбулентный):
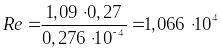 ,
,
так как Re>Reкр – то следует, что течение турбулентное.
Коэффициент потерь при турбулентном течении:
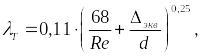
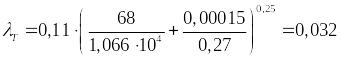
Найдём потери напора на трение:
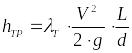 .
.
Отсюда
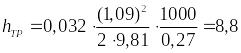 м.
м.
Задача №8.5 (325)
Расход воды определяется по формуле
![]() ,
(1)
,
(1)
где
![]() – площадь сечения трубы,
– площадь сечения трубы,
![]() – скорость в трубе.
– скорость в трубе.
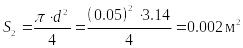
Для решения задачи воспользуемся уравнением Бернулли с учетом потерь на трение:
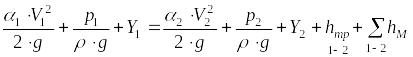 ,
(2)
,
(2)
где
![]() – коэффициенты Кориолиса,
– коэффициенты Кориолиса,
![]() –
плотность жидкости,
–
плотность жидкости,
![]() –давление
в резервуаре и трубе соответственно,
–давление
в резервуаре и трубе соответственно,
![]() – высоты искомых сечений,
– высоты искомых сечений,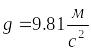
![]() –
потери напора на трение,
–
потери напора на трение,
![]() –
суммарные потери на местное сопротивлениях.
–
суммарные потери на местное сопротивлениях.
Исходя из условий задачи, в уравнении
![]() =0,
т.к. уровень воды поддерживается
постоянным;
=0,
т.к. уровень воды поддерживается
постоянным;
![]() ;
Y2=0; местным
сопротивлением
;
Y2=0; местным
сопротивлением
![]() пренебрегаем. Тогда уравнение (2) примет
вид:
пренебрегаем. Тогда уравнение (2) примет
вид:
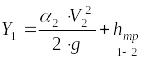 , (3)
, (3)
где
![]() ,
(4)
,
(4)
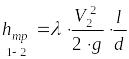 . (5)
. (5)
Подставляя в уравнение (3) выражения (4) и (5) получаем:
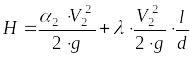 ,
(6)
,
(6)
где
![]() .
.
Теперь из уравнения (6) выражаем
![]() :
:
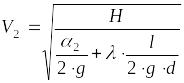 . (7)
. (7)
Находим :
 .
.
Теперь воспользуемся формулой (1) и найдем Q:
![]() .
.
Задача №8.6 (326)
Используя значение скорости
![]() ,
полученное в задаче № 8.5, определим
число Рейнольдса
,
полученное в задаче № 8.5, определим
число Рейнольдса
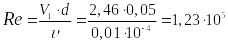 .
.
Так как полученное число Рейнольдса
превышает критическое значение
![]() значит, для нахождения
значит, для нахождения
![]() во втором приближении применим формулу
во втором приближении применим формулу
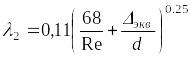 ,
,
где – эквивалентная шероховатость, т.к. труба является абсолютно гладкой то
![]() .
.
Отсюда
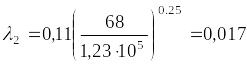 .
.
Воспользуемся уравнением Бернулли с учетом потерь на трение:
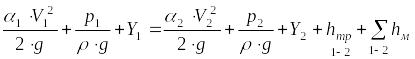 . (1)
. (1)
Исходя из условий задачи, в уравнении![]() ,
,
![]() ,
Y2=0;
местным сопротивлением
,
Y2=0;
местным сопротивлением
![]() пренебрегаем. Тогда уравнение Бернулли
примет вид:
пренебрегаем. Тогда уравнение Бернулли
примет вид:
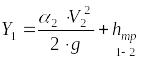 ,
,
где
![]() =Н,
=Н,
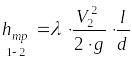 .
.
Отсюда
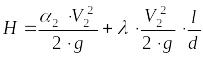 ,
,
где
![]() .
.
Из полученного уравнения выражаем
![]() :
:
. (2)
Отсюда
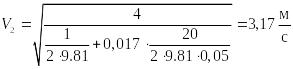 .
.
Найдем
![]() ,используя формулу:
,используя формулу:
![]() ,
(3)
,
(3)
где
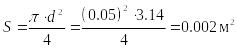 ,
,
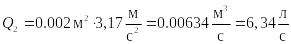 .
.
Используя значение скорости
![]() ,
полученное во втором приближении,
определим число Рейнольдса
,
полученное во втором приближении,
определим число Рейнольдса
![]()
Так как полученное число Рейнольдса
превышает критическое значение
![]() ,
значит, для нахождения
,
значит, для нахождения
![]() в третьем приближении применим формулу
в третьем приближении применим формулу
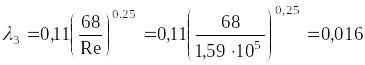 .
.
Для определения скорости
![]() ,
воспользуемся уравнением Бернулли
,
воспользуемся уравнением Бернулли
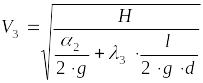 ,
,
отсюда
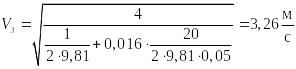 .
.
Найдем
![]() :
:
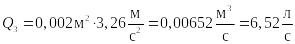 .
.
Задача №8.7 (342)
Для решения данной задачи воспользуемся уравнением Бернулли с учетом потерь на трение
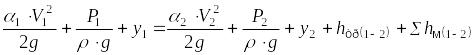 ,
,
где α1, α2 –коэффициенты, в нашем случае α1= α2 = 1; V1, V2 – скорости течения потока на входе в трубу и на выходе из нее, Р1, Р2 – давления на разных концах трубы,y1, y2 − высоты сечений относительно нулевого уровня,hтр(1-2), Σhм(1-2) − потери на трение и местные сопротивления на участке 1−2,g − ускорение свободного падения,ρ − плотность жидкости.
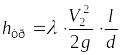 .
.
В данной формуле, из которой определяются потери на трение, λ − коэффициент потерь, l − длина трубы, d − ее диаметр. Суммарные местные потери определяются из формулы
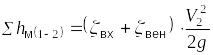 .
.
Применимо к условиям данной задачи (Р1= Р2=Ратм; y1=H; y2=0; V1=0) уравнение Бернулли упростится до вида
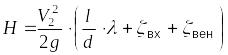 ,
,
откуда скорость потока определится как
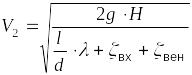 .
.
Принимая g= 9,8
![]() ,
H = 4 м,l
= 20 м, d = 0,05 м, λ =
0,03, ζвх = 0,5, ζвен =
3,5, получим
,
H = 4 м,l
= 20 м, d = 0,05 м, λ =
0,03, ζвх = 0,5, ζвен =
3,5, получим
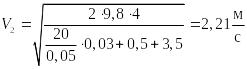 .
.
Расход жидкости определяется по формуле
Q = V2·S2 ,
где S2 − площадь выходного сечения трубы,
S2 = π·d2/4=3,14·0,052/4=0,0019625 м2.
Q = 2,21·0,0019625=0,0043371![]() =4,33
=4,33![]() .
.
Тема 9. Истечения через отверстия и насадки при постоянном напоре
Задача № 9.1 (520)
Расход жидкости через отверстие находиться по формуле:
![]() ;
;
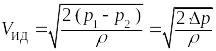 ;
;
![]() ,
,
где коэффициент поджатия
![]() =
0,6 (для малого отверстия); коэффициент
скорости
=
0,6 (для малого отверстия); коэффициент
скорости
![]() =
0,97…0,98;
=
0,97…0,98;
![]() -
скорость идеальной жидкости;
-
скорость идеальной жидкости;
![]() -
площадь отверстия, через которое
происходит утечка воды; плотность
воды
=1000кг/м3.
-
площадь отверстия, через которое
происходит утечка воды; плотность
воды
=1000кг/м3.
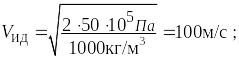
![]() ;
;
1сутки = 86400с;
=16,1м3/сутки.
Ответ: =16,1м3/сутки.
Задача № 9.2 (537)
Расход воды (без учета вязкости) через насадок определяется по формулам:
![]() ;
;
![]() ;
;
![]()
где
-
скорость идеальной жидкости;
![]() - площадь струи в насадке;
- площадь струи в насадке;
![]() =
1 - коэффициент расхода;
=
1 - коэффициент расхода;
![]()
Расход воды (с учетом вязкости) находится по формуле:
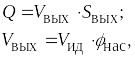
где
![]() -
скорость жидкости на выходе из насадка;
-
скорость жидкости на выходе из насадка;
![]() =
0,8 - коэффициент скорости при истечении
через насадок;
=
0,8 - коэффициент скорости при истечении
через насадок;
![]() -
площадь струи при выходе;
-
площадь струи при выходе;
![]()
Максимальный вакуум – напор в узком сечении, находится из уравнения Бернулли
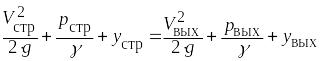 ;
;
![]() ;
;
![]() ,
,
![]() взаимно уничтожаются; из уравнения
неразрывности находим скорость струи:
взаимно уничтожаются; из уравнения
неразрывности находим скорость струи:
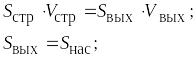
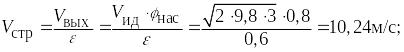
отсюда найдем максимальный вакуум
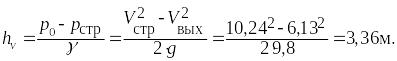
Тема 10. Нестационарные течения
10.1 Неустановившиеся течения
Задача №10.1
Запишем уравнение Бернулли:
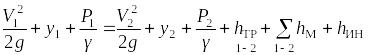 ;
;
С учётом того, что:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() - потери на трение на участке
;
- потери на трение на участке
;
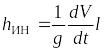 - потери напора на участке
при движении с увеличением скорости;
- потери напора на участке
при движении с увеличением скорости;![]() - потери при входе в трубу, будем иметь:
- потери при входе в трубу, будем иметь:
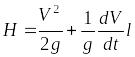 ;
;
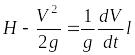 ;
;
;
![]() -скорость
стационарного течения:
-скорость
стационарного течения:
![]()
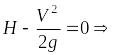 .
.
Задача №10.2
Запишем уравнение Бернулли:
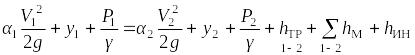 ;
;
С учётом того, что:
;
;
;
;
;
![]()
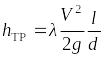 - потери на трение на участке
;
- потери напора на участке
при движении с увеличением скорости;
- потери на трение на участке
;
- потери напора на участке
при движении с увеличением скорости;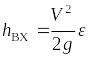 - потери при входе в трубу , будем иметь:
- потери при входе в трубу , будем иметь:
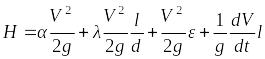 ;
;
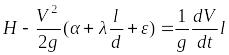 ;
;
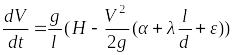 ;
;
![]() -скорость
стационарного течения:
-скорость
стационарного течения:
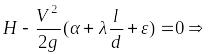
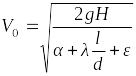 ;
;
Определим время t, за
которое скорость в трубе достигнет
![]() ;
;
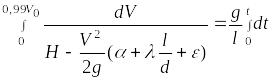 ;
;
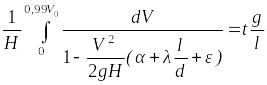 ;
;
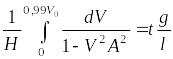 ,
где
,
где
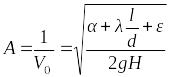 ;
;
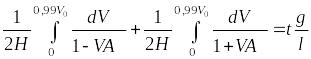 ;
;
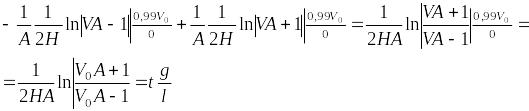
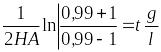 ;
;
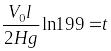 ,
следовательно,
,
следовательно,
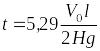 .
.
Найдём объёмный расход
![]() .
.
Используя предыдущую зависимость, запишем:
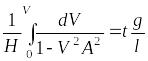 ;
;
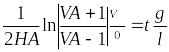 ;
;
 ;
;
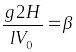 .
.
Тогда
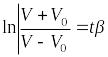 .
.
С учётом того, что
![]() ,
имеем
,
имеем
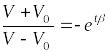 ;
;
![]() .
.
Умножим обе части на
![]()
![]() ;
;
![]() ;
;
Умножив обе части на S трубы, получим выражение для объёмного расхода:
.
Задача №10.3
Уравнение U- образной вертикальной трубки может быть представлено уравнением уравнительной башни
Рассмотрим колебания идеальной жидкости в U- образной вертикальной трубке как колебания математического маятника
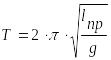 ,
,
где
![]() - приведенная длина математического
маятника.
- приведенная длина математического
маятника.
Отсюда, период колебаний
.
Задача №10.4
Запишем уравнение изменения удельной энергии между сечениями 0 – 0 и 1– 1, если пренебречь трением, имеет следующий вид:
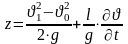 ,
(1)
,
(1)
где
 - скорость перемещения уровня в башне
площадью сечения
- скорость перемещения уровня в башне
площадью сечения
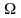 ,
,
 - скорость в штольне площадью сечения
- скорость в штольне площадью сечения
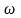 .
При этом расход
.
При этом расход
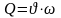 ,
равен сумме расходов
,
равен сумме расходов
 и
и
 ;
имея в виду, что
-
расход воды, поступающей к турбине,
;
имея в виду, что
-
расход воды, поступающей к турбине,
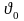 -
скорость воды в сечении 0 – 0, а также
скорость
-
скорость воды в сечении 0 – 0, а также
скорость
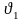 малы по сравнению со скоростью
,
их квадратами можно пренебречь. Тогда
уравнение (1) примет вид
малы по сравнению со скоростью
,
их квадратами можно пренебречь. Тогда
уравнение (1) примет вид
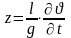 ,
(2)
,
(2)
причем в силу сказанного выше
 (3)
(3)
 (4)
(4)
На основании этих уравнений уравнение (2) может быть представлено следующим образом:
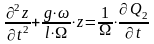 .
(5)
.
(5)
Это есть основное уравнение уравнительной башни.
Если внезапно прекратить отток воды из
башни в турбину, то
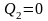 и
и
 .
При этом из (5) получим:
.
При этом из (5) получим:
 .
.
Это уравнение имеет интеграл
 .
.
Период колебаний
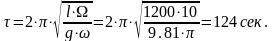
Амплитуда колебаний
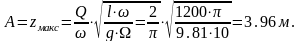
10.2. Гидравлический удар в трубах
Задача №10.5 (422)
Относительное изменение объёма связано с коэффициентом сжимаемости следующим выражением

При постоянной массе относительное изменение объёма равно

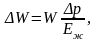
где W – внутренний объём участка трубопровода, который находится по формуле


Относительное изменение сечения трубопровода составляет
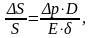

где S – площадь сечения трубопровода, которая находится по формуле

D – средний диаметр трубопровода

Тогда

Объём воды, который следует накачать в трубопровод составляет
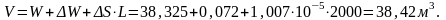
Задача №10.6 (446)
Повышение давления в области торможения жидкости находится по формуле
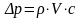 , (1)
, (1)
где - плотность воды (0,001кг/м3), с- скорость распространения фронта остановившейся жидкости от задвижки к свободному концу трубы, - скорость воды до перекрытия трубопровода.
Скорость с определяется по формуле
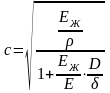 , (2)
, (2)
где
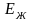 - модуль объемного сжатия воды,
- модуль упругости стали,
- модуль объемного сжатия воды,
- модуль упругости стали,
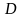 - средний диаметр трубопровода, который
определяется по формуле
- средний диаметр трубопровода, который
определяется по формуле
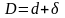 ,
,
где - внутренний диаметр трубопровода, - толщина стенки трубы.
Подставив (2) в (1), будем иметь
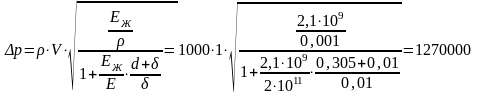 Н/м2
=
Н/м2
=
=12,7 кг/см2.
Приложения приложение №1. Параметры воздуха.
Параметры воздуха на различных высотах (стандартная атмосфера)
-
Высота Н, км
Температура
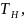 К
К

Скорость
звука
 ,
,м/сек
Кинемати-
ческая
вязкость
 м2/сек
м2/секУскорение свободного падения тела
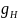 , м/сек2
, м/сек2Средний
молеку-
лярный
вес,
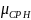
0
288,15
1,0000
1,0000
340,28
1,4607∙10-5
9,80665
28,966
0,5
284,90
9,4205∙10-1
9,5282∙10-1
338,36
1,5196
9,80511
28,966
1
281,65
8,8701
9,0751
336,43'
1,5812
9,80357
28,966
1,5
278,40
8,3460
8,6384
334,48
1,6461
9,80203
28,966
2
275,14
7,8458
8,2171
332,52
1,7146
9,80049
28,966
2,5
271,89
7,3716
7,8127
330,55
1,7866
9,79896
28,966
3
268,64
6,9208
7,4237
328,56
1,8624
9,79742
28,966
4
262,13
6,0850
6,6891
324,56
2,0271
9,79435
28,966
5
255,63
5,3338
6,0125
320.51
2,2103
9,79128
28,966
6
249,13
4,6595
5,3895
316,41
2,4153
9,78820
28,966
7
242,63
4,0560
4,8171
312,25
2,6452
9,78514
28,966
8
236,14
3,5182
4,2931
308,05
2,9030
9,78207
28,966
9
229,64
3,0388
3,8132
303,78
3,1942
9,77900
28,966
10
223,15
2,6144
3,3761
299,45
3,5232
9,77594
28,966
11
216,66
2,2393
2,9784
295,07
3,8966
9,77287
28,966
12
216,66
1,9137
2,5453
295,07
4,5595
9,76981
28,966
14
216,66
1,3979
1,8593
295,07
6,2420
9,76369
28,966
16
216,66
1,0213
1,3584
295,07
8,5437
9,75758
28,966
18
216,66
7,4630∙10-2
9,9257∙10-2
295,07
1,1694∙10-4
9,75146
28,966
20
216,66
5,4546
7,2547
295,07 295,07
1,5997
9,74537
28,966
22
216,66
3,9875
5,3033
2,1883
9,73927
28,966
24
216,66
2,9155
3,8776
295,07
2,9929
9,73318
28,966
25
219,40
2,1341
2,8030
296,93
4,1842
9,72710
28,966
28
224,87
1,5736
2,0164
300,61
5,9370
9,72102
28,966
30
230,35
1,1681
1,4613
3304,25
8,3565
9,71494
28,966
32
235,82
8,7337∙10-9
1,0676
307,84
1,1661∙10-3
9,70888
28,966
34
241,28
6,5820
7,8608∙10-3
311,38
1,6135
9,70282
28,966
36
246,74
4,9900
5,8276
314,89
2,2165
9,69676
28,966
38
252,20
3,8042
4,3465
318,36
3,0248
9,69071
28,966
40
257,66
2,9199
3,265
1,6397
321,78
4,0956
9,68466
28,966
45
271,28
1,5436
330,17
8,4977
9,66957
28,966
50
274,00
8,3475-10-4
8,7788∙10-4
331,82
1,5997∙10-2
9,65452
28,966
55
270,56
4,5166
4,8105
329,74
2,8903
9,63950
28,966
60
253,40
2,3806
2,7071
319,11
4,8749
9,62452
28,966
65
236,26
1,2006
1,4642
308,13
8,5151
9,66957
28,966
70
219,15
5,7580∙10-9
7,5712∙10-5
296,76
1,5475∙10-1
9,59466
28,966
80
185,00
1,0995
1,7126
272,66
5,9202
9,56494
28,966
90
185,00
1,8203∙10-6
2,8354∙10-6
272,60
3,5759∙100
9,53536
28,966
100
209,22
3,1987-10-7
4,4075-10-7
9,50591
28,962
120
332,24
2,5217∙10-8
1,0633∙10-8
9,43288
28,624
140
768,00
7,2887∙10-9
2,6748∙10-9
9,38948
28,314
160
1155,3
3,7628
9,0457-10-10
9,33205
27,950
180
1193
2,2199
5,0883
9,27400
27,476
200
1226,8
1,3455
2,9477
9,21750
27,000
225
1269,9
7,4584∙10-10
1,5404
9,14762
26,348
250
1302,8
4,2900
8,3835.10-11
9,07850
25,577
275
1334,6
2,5554
4,7024
9,01021
24,672
300
1358,0
1,5731
2,7364
8,94270
23,731
400
1480
5588∙10-14
0,7342
8,680
19,56
500
1576
1566
0,1806
8,428
18,28
600
1691
5240.10-15
0,5402∙10-12
8,187
17,52
700
1812
2011
0,1879∙10-12
7,957
17,03
Примечания:
Данные в приложении №1 до высоты Н = 200 км взяты по ГОСТ 4401—64.
Данные в диапазоне высот от 225 до 300 км соответствуют рекомендациям, приводимым в ГОСТ 4401—64.
При
Н = 0:
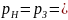 101 328,9 Н/м2
=
760мм.рт.ст.
= 10332,3 кг/м2;
101 328,9 Н/м2
=
760мм.рт.ст.
= 10332,3 кг/м2;
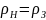 = 1,225 кг/м3
= 0,12492
= 1,225 кг/м3
= 0,12492
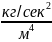 .
.
Приложение №2. Физические свойства газов.
Таблица №1.
Плотность некоторых газов при 00 и 760 мм.Рт.Ст.
Наименование газов |
|
Наименование газов |
ρ, кг/м3 |
Кислород |
1,43 |
Метан |
0,717 |
Водород |
0,09 |
Окись углерода |
1,25 |
Азот |
1,25 |
Углекислый газ |
1,98 |
Воздух |
1,29 |
Гелий |
0,179 |
Таблица №2.
Зависимость показателя адиабаты для воздуха от температуры
t 0C |
|
140 |
1000 |
20000 |
k |
1,406 |
1,405 |
1,396 |
1,283 |
Приложение №3. Международная система единиц (си)

Продолжение приложения №3.

Библиографический список
Краснов Н.Ф. Аэродинамика: в 2 ч. Ч.2:Методы аэродинамического расчета: учебник. Изд. 4-е. –М.: Книжный дом «Либроком», 2010. – 416 с.
Сидельников Р.В. Аэрогидрогазодинамика: Конспект лекций. – Челябинск: Изд-во ЮУрГУ, 2003. – 94с.
Краснов Н.Ф. Аэродинамика. Ч. 1: Основы теории. Аэродинамика профиля и крыла: Учебник. Изд. 4-е. –М.: Книжный дом «Либроком», 2010. – 496 с.
Дмитриевский А.А., Лысенко Л.Н. Внешняя баллистика. –М.: Машиностроение, 2005. –608с.
Краснов Н.Ф. и др. Прикладная аэродинамика. Под редакцией Краснова Н.Ф. Учебное пособие для втузов. М., Высшая школа, 1974. –732с.
Яблонский В.С. и Исаев И.А. Сборник задач и упражнений по технической гидромеханике. М., Физматиздат, 1963. –200с.
Давидсон В.Е. Основы газовой динамики в задачах. М., Высшая школа, 1965. –208с.
Аэродинамика в вопросах и задачах: учеб.пособие для ВТУзов /
Н.Ф. Краснов, В.Н. Кошевой, А.Н. Данилов и др. – М. : Высш. шк., 1985. – 759 с.
Краснов Н.Ф., Кошевой В.Н. Управление и стабилизация в аэродинамике: Учеб. Пособие для втузов/ Под ред. Н.Ф. Краснова. – М.: Высшая школа, 1978. –480 с.
Основы аэродинамического расчета: Учеб. пособие для студентов втузов. — М.: Высш. школа, 1981. – 496 с.
Мельников А.П. Аэродинамика больших скоростей. –М.: Воениздат, 1961, 420с.
Герман Р. Сверхзвуковые входные диффузоры. –М.: Физматгиз, 1960. –290с.
Сидельников Р.В., Тропин А.Б. Аэродинамика ракет. Расчеты и исследования аэродинамических характеристик летательных аппаратов на ЭВМ: Программно-методический учебный комплекс. Учебное пособие. – Челябинск: Изд. ЮУрГУ, 1997. – 44с.
Справочные таблицы параметров атмосферы – ГОСТ 24631–81.

 ,
кг/м3
,
кг/м3 0
0