5.2. Обтекание тел вращения с криволинейной образующей ( )

1. Метод местных конусов определения давления (или скорости) на конусе, находящемся под углом атаки к набегающему потоку

В соответствии с методом местных конусов (ММК) коэффициент давления на поверхности конуса с углом при определяется по зависимостям (5.1) или (5.2), в которых вместо ставится – угол местного конуса, определяемый формулой

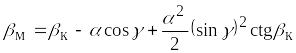, (5.4)

где – угол “исходного” конуса, обтекаемого под углом атаки ; – угол общей образующей “исходного” и местного конуса (рис.5. 2).

Рис. 5.2. Местный конус на поверхности конического тела

Местный конус – это конус (с углом ), находящийся в осесимметричном обтекании набегающим потоком (см. рис. 5.2).

Аналогично ММК используют для определения давления в точке А на теле вращения с криволинейной образующей (рис. 5.3), где – угол между касательной к криволинейной образующей (сечение по )в данной точке А и осью тела вращения.

Рис.5.3. Местный конус на криволинейной образующей

2. Ньютоновская теория

При больших сверхзвуковых скоростях набегающего потока, а также в разреженных слоях атмосферы хорошие результаты дает «Ньютоновская теория торможения», в соответствии с которой нормальная составляющая скорости набегающего потока теряется в неупругом ударе в точке контакта с обтекаемой поверхностью (рис. 5.4).

Рис.5.4. Составляющие вектора скорости

Из уравнения сохранения импульса при неупругом ударе

,

где

.

Тогда

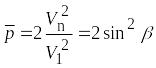. (5.6)

Так как в точке торможения ( ) коэффициент давления равен , то, заменив в формуле (12) двойку на , получим формулу

, (5.7.)

соответствующую усовершенствованной теории Ньютона.

Коэффициент давления на образующей ( )конуса с углом при обтекании его с углом определяется по зависимости

. (5.8)

Для определения отхода ударной волны на нулевой линии тока ( = 2) сферического тела можно использовать зависимости [13]:

(5.9)

или

, (5.10)

или

. (5.11)

Здесь – относительный отход волны, измеряемый в долях радиуса сферы; – относительное изменение плотности газа на скачке:

Давление в донной части

При обтекании тел вращения зависимость коэффициента давления в донной части имеет характер, показанный на рис. 5.5.

Рис. 5.5. Изменение от числа

При в соответствии с выражением для коэффициента давления имеем

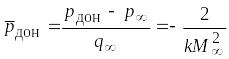, (5.9)

(кривая 1 на рис.5.5), что подтверждается при В диапазоне же изменений от 1 до (3…4) (кривая 2 рис. 5) используют зависимость

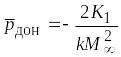, (5.10)

где – эмпирический коэффициент, зависящий от числа , удлинения, формы тела.

Аэродинамические коэффициенты для тел вращения

Сила давления на площадку (рис.5.6) определяется выражением .

Рис.5.6 Проекции сил на оси координат

Продольная ( ) и нормальная ( ) составляющие силы равны:

,

.

Суммарный продольный момент от сил и относительно вершины О

.

Тогда аэродинамические коэффициенты могут быть записаны в виде:

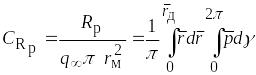, (5.11)

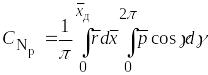, (5.12)

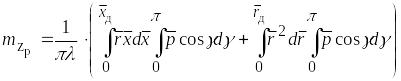, (5.13)

где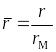 ; ; 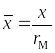; ; 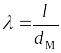– удлинение тела; 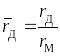, - радиус донного среза тела; .

Вычисление аэродинамических коэффициентов для конуса

Для конуса:

, (5.14)

, (5.15)

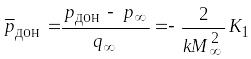где при . При определение производится в зависимости от коэффициента силы трения .

Для определения аэродинамических характеристик ЛА в целом можно воспользоваться следующими зависимостями:

Коэффициент нормальной силы

, (5.16)

где  коэффициент пересчета аэродинамических коэффициентов на новый характерный размер,  характерный размер очередного элемента входящего в состав ЛА,  характерный поперечный размер ЛА.

Производная от коэффициента нормальной силы по углу 

. (5.17)

Коэффициент силы продольного сопротивления

- для дозвуковых скоростей полета

, (5.18)

- для сверхзвуковых скоростей полета

. (5.19)

Коэффициент профильного сопротивления

, (5.20)

где  коэффициент, учитывающий форму ЛА,  фиктивное удлинение корпуса, удлинение корпуса,  характерный размер, длина корпуса ЛА,  характерный размер, диаметр корпуса ЛА.

Коэффициент силы трения

, (5.21)

где  число Рейнольдса,

 скорость набегающего потока,  характерный линейный размер ЛА (длина),  кинематический коэффициент вязкости потока,  скорость звука набегающего потока,  площадь боковой поверхности ЛА,  площадь миделевого сечения.

Коэффициент силы донного сопротивления:

- дозвуковой диапазон скоростей

, (5.22)

где , .

- сверхзвуковой диапазон скоростей

при , (5.23)

, при , (5.24)

где , , .

Коэффициент центра давления

Коэффициент аэродинамического момента

.

Коэффициент лобового сопротивления

.

Коэффициент подъемной силы

.

Задачи

№ 5.1

Конус длинной l=1м (рис. 1) с β=20°=0,349рад. и при на высоте H=0км движется под углами: 1) α=0° и 2) α=4°. Для конуса определить:

1. При α=0° силу, действующую на боковую поверхность , силу донного сопротивления и силу продольного сопротивления R.

2. При α=4°=0,06981рад силу трения , коэффициент нормальной силы и нормальную силу , действующую на конус.

Ответ: 1. Н, Н, R = 17424,48 Н. 2. Н, =0,1098, Н.

№ 5.2

О пределить N и её коэффициенты: для пластины, обтекаемой потоком под углом атаки 5 и 10 градусов. V=500 м/с на высоте 0 км. Площадь пластины в плане S=1 , длина l=1 м.

О твет: ; при Н; при Н.

№ 5.3

Рассчитать на поверхности профиля и , для профиля ромба обтекаемым потоком с М=5 , при углах атаки и . Геометрические характеристики ромба: длина b=1м и толщина .

Ответ: При , , ;при , , ,

№ 5.4

Для конуса с ,и длинной конуса м, обтекаемым потоком с М=4, на высоте h = 0 км провести расчёты:

1) При найти коэффициенты силы трения, силы давления и силы донного сопротивления. Найти суммарный коэффициент.

2) При найти по ньютоновской теории.

Ответ: ,