4.2. Косые скачки
Плотность:
.
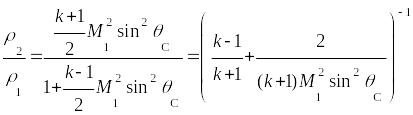Давление:
.
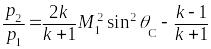Связь углов
и
(рис.4.1)
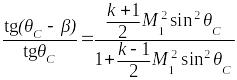
или
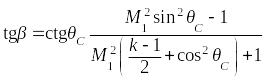
или
.
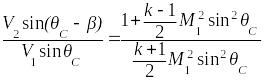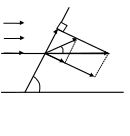
Рис. 4.1. Геометрическая интерпретация косого скачка
где
– угол косого скачка;
–угол
поворота потока за скачком;
–
скорость потока после скачка.
Задачи
№ 4.1 (2)
Звук работы двигателя зарегистрирован через t = 2,15c после пролета самолета над пунктом регистрации (рис.1). Определить скорость полёта, если высота Н=1км.
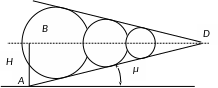
Рис.4.2. Схема распространения звука работы двигателя
Ответ: 486 м/с.
№ 4.2 (11)
По теневому фотоснимку обтекания иглы сверхзвуковым потоком воздуха измерен угол β = 28° между поверхностью слабой конической волны и направлением невозмущенного потока. Термопара, открытая навстречу потоку, показывает температуру Т0 = 289 К. Найти скорость потока V∞.
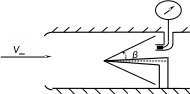
Рис.4.3. Образование области распространения малых
возмущений, ограниченной конусом Маха.
Ответ: 524м/с.
№ 4.3 (82)
Температура воздуха в форкамере сверхзвуковой трубы Т0 = 2880 К. Поток на срезе сопла трубы имеет скорость V1 = 530 м/с и обтекает препятствие с образованием прямого скачка. Найти V2 – скорость воздуха после скачка.
Ответ: V2 = 181 м/с.
№ 4.4 (83)
С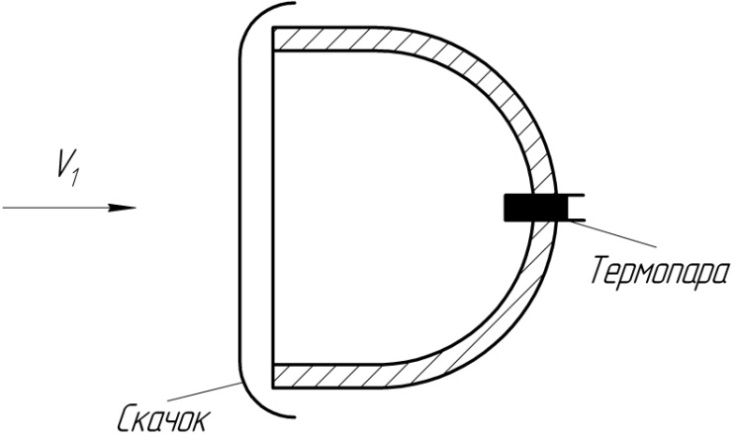
корость
воздуха, замеренная после прямого скачка
V2=280 м/с. Термопара
в кожухе показала температуру +770С.
Найти температуру воздуха в потоке до
скачка. (рис. 4.4)
Рис. 4.4. Термопара в кожухе
Ответ: Т =
.
№ 4.5 (88)
Давление, измеренное в сверхзвуковом потоке трубкой полного напора, в 12 раз больше давления, измеренного на щеке клина рис. 4.5. Найти коэффициент восстановления давления торможения в прямом скачке .
Рис. 4.5. Трубки статического и полного напоров
Ответ: = 0,33.
№ 4.6 (89)
Подсчитать давление
p02
в камере ВРД самолёта, летящего на
высоте
=10000
м со скоростью
1
=600 м/с, при наличии прямого скачка на
входе, и давлении p01,
которое получилось бы в камере, если бы
торможение было изэнтропическим?
Ответ: p01 = 2,06 ата, p02 = 1,55 ата.
№ 4.7 (96)
Трубка полного напора, установленная на самолете, показывает на высоте 15000 м абсолютное давление 71 100 Н/м2. Найти скорость полета.
Ответ: V=2180 км/ч.
№ 4.8 (121)
Струя воздуха со скоростью V1=700 м/с из баллона с температурой Т0 =288 К возникает плоский скачок под углом θс = 50° к направлению скорости до скачка. Найти скорость V2 после скачка и угол отклонения потока в скачке.
Ответ: V2=
,
θс=
.
№ 4.9 (123)
Скорость невозмущенного потока воздуха,
обтекающего клин с полууголом раствора
,
равна
.
Угол наклона косого скачка
измерен
по фотографии. Геометрическим построением
найти
–
скорость потока за скачком. Также решить
задачу аналитически.
Ответ:
.
Тема 5. Сверхзвуковое обтекание тел вращения
5.1. Обтекание конуса сверхзвуковым потоком
Решается задача определения скорости
и других параметров газа на поверхности
конуса при
.
Решение ведется для заданных чисел
набегающего потока и углов
полураствора
конуса, когда скачок является прямолинейным,
коническим (рис.5.1)
В основе решения задачи лежат уравнения,
неразрывности и движения, записанные
в полярной системе координат в
дифференциальной форме. В этой системе
координат можно их записать наиболее
просто, используя свойство коничности
течения (в области между коническим
скачком и поверхностью конуса), т.е.
независимости параметров от координаты
.
Рис.5.1. Схема обтекания конуса
Совместное решение уравнений неразрывности и движения дает:
,
,
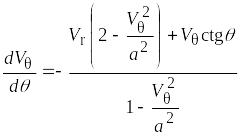а из уравнения энергии следует:
, 
Задавшись числом
и углом
ищут соответствующий
и
на поверхности конуса из условия, что
при
.
Вычисление скоростей на поверхности
ведут по формулам
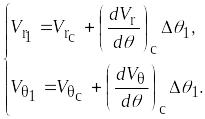
Аналогично ведутся вычисления скоростей
на других промежуточных поверхностях
.
При
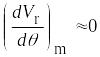процесс вычислений останавливают,
полагая, что
,
.
По
вычисляются давления на конусе
и
.
Аппроксимация результатов расчетов, выполненная Красновым Н.Ф.[1] , дает выражение
,
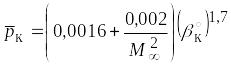(5.1)
которое удовлетворительно согласуется
с экспериментом при
.
Другая формула, приведенная Мельниковым А.П. [11],
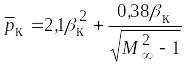, (5.2)
дает хорошие результаты для всех , пока скачок является присоединенным.
Определение угла скачка уплотнения на конусе можно сделать по формуле, приведенной Германом Р. [12],
, (5.3)
где
– угол поворота потока за скачком
уплотнения. Соотношение (5.3) совместно
с соотношением для косого скачка
устанавливает связь между углами
и
через число
набегающего потока.
Более удобными могут оказаться зависимости [13]
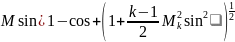
или
.
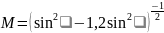Температура и скорость на поверхности конуса
Температура
на поверхности конуса может быть
определена по зависимости
,
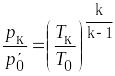где давление торможения газа, прошедшего
скачек (
),
определяется через коэффициент
восстановления
в соответствии с теорией косого скачка:
.
Скорость на поверхности конуса можно определить из уравнения энергии
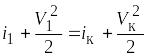
по параметрам набегающего потока
и энтальпии
на поверхности конуса.