Переваги й недоліки критерію окупності

Переваги	Недоліки
1	2
• Простота розрахунку	• Прив'язка до облікових даних (зазвичай доход визначають не за грошовими потоками, а за даними бухгалтерського обліку)
• Простота для розуміння й традиції застосування	• Інвестиції проводять для одержання вигоди, що перевищує витрати. Критерій окупності показує, коли інвестор зможе "повернути своє", і нічого не говорить про те, яку вигоду принесе проект за межами строку окупності. У результаті інвестиційна пропозиція з меншим строком окупності може здатися більш кращою, ніж варіант, здатний принести більший сумарний доход
• Відповідність загально-прийнятим методам бухобліку й, як наслідок, доступність вихідної інформації	• Ризик ураховується лише побічно (різниця між тривалістю життєвого циклу проекту й строком окупності — це "запас часу" для того, щоб проект став економічно вигідним)
	• Не враховується альтернативна вартість використовуваних для проекту ресурсів (грошових, кадрових, інформаційних і т.д).
	• Неаддитивність (окупність проекту не рівна сумі окупності його етапів)

Метод простої норми прибутку (Accounting Rate of Return — ARR). При використанні цього методу середня за період життя проекту чистий бухгалтерський прибуток зпівставляється із середніми інвестиціями (витратами основ­них й оборотних коштів) у проект.

Метод простий для розуміння й включає нескладні обчис­лення, завдяки чому може бути використаний для швидкого відбраковування проектів. Однак істотним недоліком є те, що ігнорується негрошовий (прихований) характер деяких видів витрат (типу амортизаційних відрахувань) і пов'язана з цим податкова економія; доходи від ліквідації старих активів, замінених новими; можливості реінвестування одержуваних доходів і тимчасова вартість грошей. Метод не дає можливості судити про перевагу одного із проектів, що мають однакову просту бухгалтерську норму прибутку, але різні величини се­редніх інвестицій.

ARR = , (11.2)

де: Р₆ — чистий бухгалтерський прибуток від проекту;

ІС — інвестиції.

Метод NPV. Даний метод заснований на використанні поняття чистого сучасного значення вартості (Net Present Value).

Визначається різниця між сумою дисконтних грошових надходжень від реалізації проекту й дисконтної поточної вар­тості всіх витрат.

NPV = (або І_о) , (11.3)

де: I_t — інвестиційні витрати в момент часу t;

CF_t — грошовий потік у період L

Іноді можна використати еквівалентний аннуітет, якщо проекти мають різну тривалість:

ЕА = 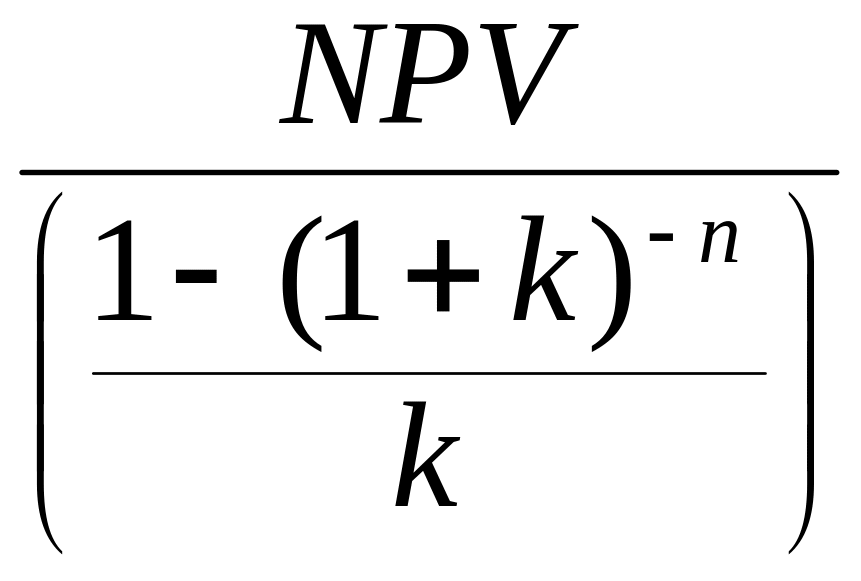(11.4)

Переваги критеріїв дисконтування:

□ ураховується альтернативна вартість використовуваних ресурсів;

□ у розрахунок приймаються реальні грошові потоки, а не умовні бухгалтерські величини, тобто оцінка інвес­тиційних проектів проводиться з позиції інвестора й не залежить від облікової політики;

□ оцінка інвестиційних проектів проводиться, виходячи з мети забезпечення добробуту власника підприємства-акціонера.

Недоліки критеріїв дисконтування (виникають із вихідних припущень):

□ підвищення акціонерної вартості підприємства — не єди­на мета підприємства (крім того, існують маркетингові, соціальні, науково-технічні, психологічні й інші цілі), от­же, обмежуватися винятково фінансовими критеріями не можна: на додаток до них у системі контроллінгу повинні використовуватися й інші критерії, що оцінюють фактори психологічного, соціального, науково-технічного плану;

□ менеджери не завжди діють раціонально й не завжди прагнуть до цього; цілі менеджерів не завжди збігаються із цілями фірми;

□ деякі з використовуваних ресурсів важко оцінити в грошовому вираженні (наприклад такі, як час висококва­ліфікованих співробітників).

Типові вхідні грошові потоки:

□ додатковий обсяг продажів і збільшення ціни товару;

□ зменшення валових витрат (зниження собівартості то­вару);

□ залишкове значення вартості устаткування наприкінці останнього року інвестиційного проекту (тому що устат­кування може бути продане або використане для іншого проекту);

□ вивільнення оборотних коштів .наприкінці останнього року інвестиційного проекту (закриття рахунків дебі­торів, продаж залишків товарно-матеріальних запасів, продаж акцій та облігацій інших підприємств).

Типові вихідні грошові потоки:

□ початкові інвестиції в перший рік (роки) інвестиційного проекту;

□ збільшення потреб в оборотних коштах в перший рік (роки) інвестиційного проекту (збільшення рахунків дебіторів для залучення клієнтів, придбання сировини й комплектуючих для початку виробництва);

□ ремонт і технічне обслуговування устаткування;

□ додаткові невиробничі витрати.

При оцінці доцільності інвестицій обов'язково встановлю­ють (розраховують) ставку дисконту, тобто процентну ставку, що характеризує норму прибутку, відносний показник міні­мального щорічного доходу інвестора, на яку він сподівається. За допомогою NPV-методу можна визначити не тільки ко­мерційну ефективність проекту, а й розрахувати ряд додатко­вих показників. Настільки велика область застосування й відносна простота розрахунків забезпечили NPV-методу ши­роке поширення, він є одним зі стандартних методів розрахун­ку ефективності інвестицій, рекомендованих до застосування ООН і Всесвітнім банком.

Однак коректне використання NPV-методу можливо тільки при дотриманні ряду умов:

Обсяг грошових потоків у рамках інвестиційного проекту повинен бути оцінений для всього планового періоду й прив'язаний до певних тимчасових інтервалів. Грошові потоки в рамках інвестиційного проекту повинні розглядатися ізо­льовано від іншої виробничої діяльності підприємства, тобто характеризувати тільки платежі й надходження, безпосеред­ньо пов'язані з реалізацією даного проекту. Принцип дискон­тування, який застосовується при розрахунку чистого наведе­ного доходу, з економічної точки зору має на увазі можливість необмеженого залучення й вкладення фінансових коштів по ставці дисконту. Використання методу для порівняння ефек­тивності декількох проектів припускає використання єдиної для всіх проектів ставки дисконту і єдиного тимчасового інтервалу (обумовленого, як правило, як найбільший строк ре­алізації з наявних).

При розрахунку NPV, як правило, використовується по­стійна ставка дисконтування, однак залежно від обставин (на­приклад, очікується зміна рівня процентних ставок) ставка дисконтування може диференціюватися по роках. Якщо в ході розрахунків застосовуються різні ставки дисконтування, то проект, прийнятний при постійній ставці дисконтування, мо­же стати неприйнятним.

Будучи абсолютним показником, NPV має найважливішу властивість — властивість аддитивності, тобто NPV різних про­ектів можна підсумувати. До числа інших найважливіших влас­тивостей цього критерію варто віднести більш реалістичні при­пущення про ставку реінвестування вступників коштів. (У методі NPV неявно передбачається, що кошти, що надходять від реалізації проекту, реінвестуються по заданій нормі дисконту г).

Використання критерію NPV теоретично обґрунтовано, і в цілому він уважається найбільш коректним вимірником ефек­тивності інвестицій. Разом з тим він має свої недоліки. Напри­клад, NPV не є абсолютно правильним критерієм при:

а) виборі між проектом з більшими первісними витратами й проектом з меншими первісними витратами при однаковій величині чистої дійсної вартості;

б) виборі між проектом з більшою чистою дійсною вартістю й тривалим періодом окупності й проектом з меншою чистою дійсною вартістю й коротким періодом окупності. Тоб­то метод NPV не дозволяє судити про поріг рентабельності й запас фінансової міцності проекту.

Метод не поєднує вплив змін вартості нерухомості й сиро­вини на чисту дійсну вартість проекту. Його використання ус­кладнюється труднощами прогнозування ставки дисконту­вання (середньозваженої вартості капіталу) і/або ставки банківського відсотка.

Таким чином, застосування абсолютних показників при аналізі проектів з різними вихідними умовами (первісними інвестиціями, строками економічного життя й ін.) може при­зводити до ускладнень при прийнятті управлінських рішень.

Тому поряд з абсолютним показником ефективності інве­стицій NPV використовуються також і відносні — індекс рен­табельності й внутрішня норма прибутковості.

Метод рентабельності інвестицій (Profitability Index — PI). Абсолютна ефективність капітальних витрат показує за­гальну величину їхньої віддачі (результативності) на підпри­ємстві, її розрахунок необхідний для оцінки очікуваного або фактичного ефекту від реальних інвестицій за певний момент часу.

Застосовують два взаємозалежних показники, за якими визначають абсолютну ефективність інвестицій. Перший (прямий) — коефіцієнт економічної ефективності (прибутко­вості). Другий (зворотний), згаданий вище — дисконтний період окупності.

Метод розрахунку індексу прибутковості (рентабель­ності) інвестицій (РІ) розраховується за формулою:

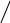РІ = 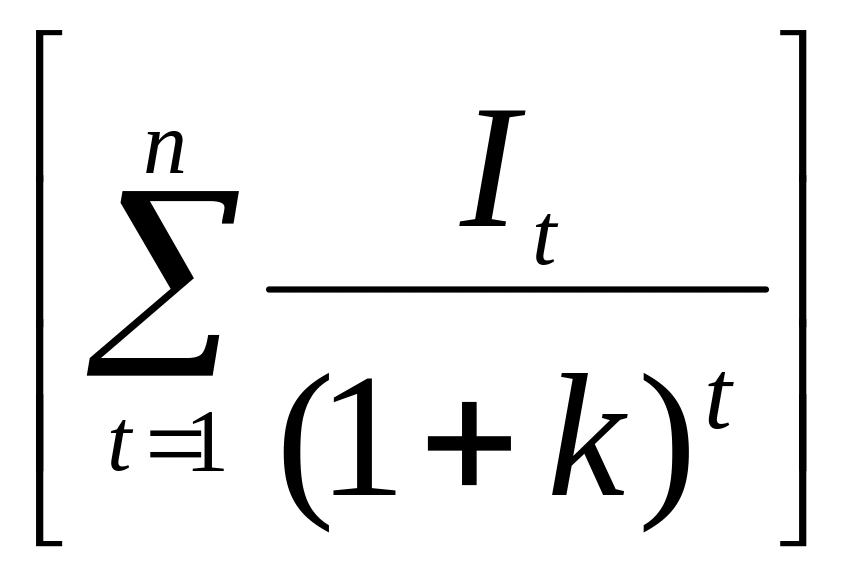(або І_о) (11.5)

або

РІ = : ІС (11.6)

де: ІС — вихідна інвестиція;

P_k — грошовий потік.

Очевидно, що якщо:

РІ>1, то проект варто прийняти;

РІ<1, то проект варто відкинути;

РІ=1, то проект ні прибутковий, ні збитковий.

На відміну від чистого сучасного значення індекс прибут­ковості є відносним показником. Завдяки цьому він дуже зручний при виборі одного проекту з ряду альтернативних, що мають приблизно однакове значення NPV, або при комплекту­ванні портфеля інвестицій з максимальним сумарним значен­ням NPV.

Переваги методу:

• простота розрахунку;

• відповідність загальноприйнятим методам бухобліку й, як наслідок доступність вихідної інформації;

□ простота для розуміння й традиційність використання. Недоліки:

□ не враховується вартість грошей у часі;

□ прив'язка до умовних бухгалтерських величин (прибу­ток замість грошових доходів);

□ показник ураховує відносні, а не абсолютні величини (рентабельність може виявитися великою, у той час як прибуток — малим);

□ ризик ураховується лише побічно (перевищення розра­хункової рентабельності над мінімально прийнятною ве­личиною — це "запас", що показує, на скільки ми маємо право помилитися);

• не враховується альтернативна вартість використовува­них для проекту ресурсів (грошових, кадрових, інфор­маційних і т.д.);

• неаддитивність (рентабельність проекту не дорівнює сумі величин рентабельності його етапів).

Метод розрахунку внутрішньої норми рентабель­ності. (Internal Rate of Return — IRR). Внутрішня норма прибутковості — найбільш широко використовуваний кри­терій ефективності інвестицій. Під внутрішньою нормою при­бутковості розуміють значення ставки дисконтування г, при якому чиста сучасна вартість інвестиційного проекту дорів­нює нулю:

IRR = r, при якому NPV = f(r) = 0.

Таким чином, IRR обчислюється з рівняння:

NPV = - І_о = 0 . (11.7)

Зміст розрахунку цього коефіцієнта при аналізі ефектив­ності планованих інвестицій полягає в наступному: IRR пока­зує максимально припустимий відносний рівень витрат, які можуть бути асоційовані з даним проектом. Наприклад, якщо проект повністю фінансується за рахунок позички ко­мерційного банку, то значення IRR показує верхню межу при­пустимого рівня банківської процентної ставки, перевищення якого робить проект збитковим.

При NPV = 0 сучасна вартість проекту (PV) дорівнює по абсолютній величині первісним інвестиціям І₀, отже, вони оку­паються. У загальному випадку чим вище величина IRR, тим більша ефективність інвестицій. Величину IRR порівнюють із заданою нормою дисконту г. При цьому якщо IRR > r, то про­ект забезпечує позитивну NPV і прибутковість, рівну IRR-r. Якщо IRR<r, витрати перевищують доходи, і проект буде збитковим.

Для оцінки внутрішньої норми окупності можна викорис­тати графік чистої дисконтної вартості, відзначивши одну не­гативну й одну позитивну точку й з'єднавши їх лінією (рис. 11.1). Для проекту, у якого відтік (інвестиція) змінюється при­пливами, у сумі переважаючий цей відтік, функція у = f® є по­нижаючою, тобто з ростом г графік функції прагне до осі аб­сцис і перетинає її в деякій точці, що є IRR. (Функція може мати кілька точок перетинання з віссю X). Перетинання з віссю X (NPV=0) дасть приблизну (а не точну) оцінку внутрішньої норми окупності.

Рис. 11.1. Оцінка внутрішньої норми окупності

Вісь ординат (r=0) графік NPV перетинає в точці, рівній сумі всіх елементів недисконтного грошового потоку, включа­ючи величину вихідних інвестицій.

Важливим моментом є те, що критерій IRR не має влас­тивість аддитивності.

На практиці будь-яке підприємство фінансує свою діяль­ність, у тому числі й інвестиційну, з різних джерел. Як плату за користування авансованими в діяльність підприємства фінансовими ресурсами воно сплачує відсотки, дивіденди, винагороди й т.п., тобто несе деякі обґрунтовані витрати па підтримку свого економічного потенціалу. Показник, що ха­рактеризує відносний рівень цих витрат, можна назвати вартістю авансованого капіталу (ВАК). Цей показник відоб­ражає сформований на підприємстві мінімум повернення на вкладений у його діяльність капітал, його рентабельність і розраховується за формулою середньої арифметичної зваже­ної.

Економічний зміст цього показника полягає в наступно­му: підприємство може приймати будь-які рішення інвес­тиційного характеру, рівень рентабельності яких не нижче по­точного значення показника ВАК (або ціни джерела коштів для даного проекту, якщо він має цільове джерело). Саме з ним порівнюється показник IRR, розрахований для конкрет­ного проекту, при цьому зв'язок між ними такий.

Якщо:

IRR > СС, то проект варто прийняти;

IRR < СС, то проект варто відкинути;

IRR = СС, то проект ні прибутковий, ні збитковий.

Незалежно від того, із чим рівняється IRR, очевидно: про­ект приймається, якщо його IRR більше деякої граничної ве­личини; тому за інших рівних умов, як правило, більше зна­чення IRR уважається кращим.

Сучасні табличні процесори дозволяють швидко й ефек­тивно визначити цей показник шляхом використання спеці­альних функцій. Однак якщо в розпорядженні аналітика не­має спеціалізованого фінансового калькулятора, практичне застосування даного методу ускладнено. У цьому випадку за­стосовується метод послідовних ітерацій з використанням табульованих значень дисконтних множників. Для цього за до­помогою таблиць вибираються два значення коефіцієнта дисконтування r₁< r₂ таким чином, щоб в інтервалі (r₁, r₂) функція NPV=f(r) змінювала своє значення з "+" на "-" або з "-" на "+". Далі застосовують формулу

IRR = r₁ + , (11.8)

де: r₁ — значення табульованого коефіцієнта дисконтування, при якому f(r₁)>0 (f(r₁)<0);

r₂ — значення табульованного коефіцієнта дисконтування, при якому f(r₂)<ПРО f(r₂)>0).

Точність обчислень обернено пропорційна довжині інтер­валу (r₁, r₂), а найкраща апроксимація з використанням табульованих значень досягається у випадку, коли довжина інтер­валу мінімальна (дорівнює 1%), тобто r₁ й r₂ — найближчі один до одного значення коефіцієнта дисконтування, що за­довольняють умовам (у випадку зміни знака функції з "+" на "-":

r₁ — значення табульованного коефіцієнта дисконтування, який мінімізує позитивне значення показника NPV, тобто f (r₁)=minr{f (r)>0};

r₂ — значення табульованого коефіцієнта дисконтування, який максимізує негативне значення показника NPV, тобто f (r₂)=maxr{f (r)<0}.

Шляхом взаємної заміни коефіцієнтів r_t й r₂ аналогічні умови виписуються для ситуації, коли функція змінює знак з "-" на "+".

Рядом позитивних властивостей:

1. показник IRR, що розраховується у відсотках, більш зручний для застосування в аналізі, ніж показник NPV, тому що відносні величини легше піддаються інтерпретації;

2. несе в собі інформацію про приблизну величину межі безпечності проекту.

У той же час критерій IRR має істотні недоліки:

1. нереалістичне припущення про ставку реінвестування. На відміну від NPV критерій внутрішньої норми прибутко­вості неявно припускає реінвестування одержуваних доходів по ставці IRR, що навряд чи здійснено в реальній практиці.

2. можливість існування декількох значень IRR. У загаль­ному випадку, якщо аналізується єдиний або кілька незалеж­них проектів з ординарним грошовим потоком, коли після первісних витрат випливають позитивні припливи коштів, за­стосування критерію IRR завжди призводить до тих же ре­зультатів, що й NPV. Але у випадку чергування припливів коштів з відтоками для одного проекту можуть існувати кілька значень IRR.

3) сильно чутливий до структури потоку платежів і не завжди дозволяє однозначно оцінити взаємовиключні проекти.

Метод розрахунку чистої термінальної вартості (Net Terminal Value — NTV). Критерій NPV заснований на приве­денні грошового потоку до початку дії проекту, тобто в його основі закладена операція дисконтування. Очевидно, що можна скористатися й зворотною операцією — нарощенням.

Рис. 11.2. Грошові потоки в методі розрахунку NTV

У цьому випадку елементи грошового потоку будуть приводи­тися до моменту закінчення проекту.

Очевидно, формула розрахунку критерію має вигляд:

NTV = - IC(1+r)ⁿ . (11.9)

Умови прийняття проекту на основі критерію NTV такі ж, як у випадку з NPV. Якщо:

NTV > 0, то проект варто прийняти; .

NTV < 0, то проект варто відкинути;

NTV = 0, то проект ні прибутковий, ні збитковий.

Критерії NPV й NTV взаємозворотні, вони дублюють один одного, тобто відбір проекту за одним з них дає такий же ре­зультат, як і при використанні іншого критерію.

Модифікована внутрішня норма прибутковості (Modified Internal Rate of Return — MIRR). Основний не­долік, властивий IRR відносно оцінки проектів з неординар­ними грошовими потоками, може бути переборений за допо­могою аналога IRR, що прийнятний для аналізу будь-яких проектів, — MIRR. Цей метод являє собою модифікацію мето­ду внутрішньої ставки рентабельності, що розширює можли­вості останнього.

MIRR — це ставка в коефіцієнті дисконтування, що врівноважує припливи й відтоки коштів по проекту. Всі гро­шові потоки доходів приводяться до майбутньої (кінцевої) вартості за середньозваженою ціною капіталу, складаються, сума приводиться до дійсної вартості по ставці внутрішньої рентабельності; з дійсної вартості доходів віднімається дійсна вартість грошових витрат й обчислюється чиста дійсна вар­тості проекту, що зіставляється з дійсною вартістю витрат.

Метод дає більш правильну оцінку ставки реінвестування й знімає проблему множинності ставки рентабельності.

Загальна формула розрахунку має вигляд:

, (11.10)

де: COF_i — відтік коштів в і-му періоді (по абсолютній величині);

СIF_i — приплив коштів в і-му періоді;

r — вартість джерела фінансування даного проекту;

п — тривалість проекту.

Майбутня (термінальна) вартість сьогоднішніх надход­жень обчислюється за формулою:

FV = = (11.11)

де r — ставка, по якій реінвестуються грошові припливи від проекту в міру їхнього надходження (або ринкова прибутковість, доступна інвесторові).

Вартість відтоків коштів:

PV = − (11.12)

то,

PV = .

Звідки: MIRR = − 1

Критерій MIRR повною мірою узгоджується із критерієм NPV і тому може бути використаний для оцінки незалежних проектів. Що стосується альтернативних проектів, то про­тиріччя між критеріями NPV й MIRR можуть виникати, якщо проекти істотно відмінні за масштабами, тобто значення еле­ментів одного потоку значно більші за абсолютною величиною іншого, або проекти мають різну тривалість. У цьому випадку рекомендується застосовувати критерій NPV, не забуваючи одночасно про облік небезпечності грошового потоку.

Дисконтний строк окупності інвестицій (Discounted Payback Period — DPP). Деякі фахівці при розрахунку показ­ника строку окупності інвестицій (РР) рекомендують урахо­вувати часовий аспект. У цьому випадку в розрахунок прий­маються грошові потоки, дисконтовані за показником WACC (середньозважена вартість капіталу). Таким чином, визна­чається момент, коли дисконтовані грошові потоки доходів зрівняються з дисконтованими грошовими потоками витрат.

Формула розрахунку DPP має вигляд:

DPP = min п, при якому ≥ IC

Очевидно, що у випадку дисконтування строк окупності збільшується.

Позитивними сторонами методу DPP є те, що він, як і кри­терій РР, дозволяє судити про ліквідність і ризикованість про­екту. Крім того, критерій DPP ураховує можливість реінвестування доходів і тимчасову вартість грошей. Недолік — ігнорує грошові надходження після закінчення строку окупності про­екту.

У цілому методи дисконтування досконаліші, ніж тра­диційні: вони відображають закони ринку капіталу, дозволяю­чи оцінити упущену вигоду від вибору конкретного способу використання ресурсів, тобто економічну вартість ресурсів. Однак у чистому вигляді ці критерії можуть використовувати­ся тільки в умовах "зробленого ринку": для аналізу інвестицій в умовах невизначеності, неповної інформації будуть потрібні модифікації критеріїв. Основна проблема, що постає при ви­користанні критеріїв дисконтування грошових потоків, — вибір ставки дисконтування.

Ставка дисконтування повинна відображати альтернатив­ну вартість капіталу, тому вона залежить від можливостей вкладення капіталу, наявних у підприємства. У літературі зустрічається безліч різних підходів до визначення ставки дисконтування. Розглянемо найпоширеніші (середньозваже­на вартість капіталу, відсоток по позиковому капіталі, ставка по безпечних вкладах й ін.) і приведемо оцінку достоїнств і не­доліків кожного підходу.

Аналіз беззбитковості й цільове планування прибутку є невід'ємною частиною інвестиційного проектування. Цей тип аналізу показує принципове виконання проекту й одночасно дозволяє з'ясувати основні вузькі місця проекту в змісті досяг­нення заданого значення прибутку, що забезпечує необхідну ефективність інвестиційного проекту.

Як показує практика, найбільш ефективні ті проекти, відповідно до яких виробництво функціонують на рівні близь­кому до рівня повної потужності. Однак, незважаючи на це, деякі проекти приносять збитки протягом перших декількох років після їхньої реалізації — з роками ситуація поліп­шується, у той час, як інші продовжують працювати зі збитком досить довго. Причин для настільки поганих результатів може бути дуже багато, наприклад: затримки в реалізації; дефекти в схемі проекту; дефіцит основних елементів; погана якість си­ровини; недостатній обсяг ринку; погана якість продукції; цінова система й т.д.

Якщо проект функціонує на більш низькому рівні викорис­тання виробничих потужностей, доходи не можуть покрити всі витрати. Коли рівень використання виробничих потужностей зростає, то можна сподіватися, що буде досягнута ситуація, коли загальні доходи будуть дорівнюють загальним витратам. У цій точці немає ні прибутку, ні збитків. Така ситуація нази­вається ситуацією беззбитковості. У такий спосіб ми підходи­мо до поняття беззбитковості.

Аналіз беззбитковості або аналіз витрат, прибутку й обся­гу виробництва, як його іноді називають, — це аналітичний підхід до вивчення взаємозв'язку між витратами й доходами при різних рівнях виробництва.

Аналіз беззбитковості використовується не тільки для цілей інвестиційного проектування. Цей аналіз корисний та­кож для поточного управління, тому що він забезпечує інформацією для ухвалення рішення шляхом аналізу впливу змін у ціні продукції, виробництві й обсягах продажів і вит­ратах, а так само прогнозування прибутків, збитків і потоків коштів.

Звернемося тепер до менш розповсюдженого в цей час джерела довгострокового фінансування — публічної емісії акцій й облігацій.

Принципово українське підприємство може розглядати питання про публічну емісію акцій або на українському ринку, або на іноземному ринку. Це дозволяє йому комбінувати одер­жання коштів з різних джерел, приводить до диверсифікованості складу акціонерів при цьому, що жоден інвестор не має контрольного пакета акцій, збільшує ліквідність продаваних акцій і служить відмінною рекламою для підприємства у ви­падку успіху.

В той же час публічна емісія акцій припускає додаткові витрати, пов'язані з високою вартістю підготовки й витратами на емісію, на рекламу й т.д. Крім того, заздалегідь не відомо, скільки грошей буде отримано, якщо тільки акції не розміщені попередньо в одного або декількох покупців.

Українські приватні особи звичайно купують дуже неве­ликий відсоток акцій. Більшість акцій продається українсько­му й іноземному портфельному інвестору.

Публічна емісія на іноземному ринку дає можливість до­ступу до джерела капіталів в усьому світі, оцінки вартості акцій на міжнародних ринках і є відмінною рекламою для підприємства у випадку успіху. На жаль, вона дорожча публіч­ної емісії на українському ринку і можлива тільки для вели­ких, добре відомих підприємств.

Пряма емісія цінних паперів, через законодавчі обмежен­ня по цінних паперах і сучасній ринковій кон'юнктурі, не дає українським підприємствам можливості одержувати гроші шляхом прямої емісії акцій на більшості іноземних ринків.

Облігації є інвестиційними інструментами, які відрізня­ються від акцій тим, що:

• по них проводиться фіксована виплата відсотків;

• вони мають фіксований термін дії;

• установлено виплату основної суми при погашенні;

• по облігаціях діє переважна вимога відносно активів при невиконанні зобов'язань.

Випуск облігацій надзвичайно малий в Україні й дуже до­рогий — потрібно виплачувати високі відсотки для того, щоб покрити ризики інвесторів.

Спочатку розглянемо це завдання в класичному варіанті для так званих купонних облігацій. Відповідно до умов інвес­тування в ці боргові фінансові інструменти підприємство, емітент облігацій зобов'язується проводити періодичний про­центний платіж на річній або піврічній основі й погасити номінальну вартість облігації на призначений термін закінчен­ня дії облігацій. Купонна облігація має такі характеристики:

□ номінальну вартість;

□ строк до погашення;

□ процентну ставку;

□ умови виплати відсотків (періодичність виплат).

Сутність оцінки вартості облігації полягає в тому, що про­тягом строку існування облігації її власник повинен одержати ту ж суму, що він вклав в облігацію при покупці. Особливість полягає в тому, що сукупність платежів, які повинен одержати власник облігації, розтягнута у часі і, отже, всі майбутні гро­шові потоки необхідно продисконтувати до моменту часу, для якого проводиться оцінка вартості облігації. Як показник дис­конту необхідно приймати прибутковість аналогічних фінан­сових інструментів.

Математична модель оцінки грошової вартості облігацій заснована на дисконтуванні грошових потоків, які виплачу­ються протягом усього строку до погашення. Вартість облігації в даний момент часу дорівнює дисконтній сумі всіх грошових потоків, з нею пов'язаних:

V_B = , (11.13)

де: М — номінальна вартість облігацій, вона ж — вартість у момент погашення;

INT — річний процентний платіж;

K_d — прибутковість на ринку позичкового капіталу ана­логічних облігацій (використовується як показник дисконтування).

Приклад 1. Нехай випущена облігація зі строком погашен­ня через 20 років. Номінал облігації дорівнює $1,000, а річна процентна ставка, що визначає величину річного процентного платежу, становить 14 відсотків. Середня процентна ставка на ринку облігацій даного типу становить також 14%. Необхідно знайти оцінку вартості облігації.

Оскільки за умовою процентний платіж проводиться один раз у рік, величина цього платежу $140. На ринку позич­кового капіталу прибутковість становить 14%. Отже, для оцінки вартості облігації ми повинні привести до теперішньо­го часу всі щорічні" процентні платежі й виплату номіналу на­прикінці двадцятого року. Скориставшись формулою (5.1), одержимо:

V_B = = 140 ∙ 6,6231 + 1000 ∙ 0,0728 = $ 1,000 .

Нехай пройшло 5 років, а процентна ставка на розглянуто­му ринку позичкового капіталу не змінилася. Скільки буде ко­штувати дана облігація? Для відповіді на це питання потрібно знайти сучасну вартість всіх платежів, що залишилися, вклю­чаючи номінал облігації, що повинен бути виплачений інвес­торові через 15 років. За аналогією одержимо:

V_B = = 140 ∙ 6,1422 + 1,000 ∙ 0,1401 = $ 1,000 .

Вартість облігації закономірно залишилася рівною її номіна­лу, тому що ситуація на ринку не змінилася. Ясно, що така си­туація збережеться протягом усього строку до погашення облігації.

Припустимо тепер, що середня ринкова ставка збільшилася на 2 відсотки й становить 16%, до погашення облігації залиши­лося 15 років. У цьому випадку прибутковість даної облігації нижче середньої по ринку і, отже, ринкова ціна облігації повин­на зменшитися. Це підтверджується розрахунками:

V_B = = 140 ∙ 5,5755 + 1,000 ∙ 0,1079 = $ 888,47 .

Якщо тепер розглянути протилежну ситуацію, коли серед­ня по ринку процентна ставка зменшилася на 2 відсотки й ста­новить 12%, то варто очікувати підвищення ринкової ціни цієї облігації, тому що вона приносить прибутковість більшу, ніж середня по ринку. Справді:

V_B = = 140 ∙ 6,8109 + 1,000 ∙ 0,1827 = $ 1136,23 .

Легко перевірити, що для обох розглянутих випадків, як­що ситуація на ринку залишається без зміни (тобто збері­гається 16% або 12%), вартість облігації наближається до номінального значення.

Якщо виплата відсотків по облігації проводиться два рази в рік, то розрахункова формула зміниться:

V_B = (11.14)

тобто дисконтувати необхідно всі піврічні виплати відповідно до піврічної процентної ставки.

Для умов попереднього прикладу, коли процентна ставка становить 12% і до погашення залишається 15 років при піврічній виплаті відсотків, одержимо:

V_B = = 70 ∙ 13,7648 + 1,000 ∙ 0,1741 = $ 1137,64 .

У цьому випадку вартість облігації виявилася трохи ви­щою, тому що процентні платежі інвестор одержує частіше. І отже, при зростанні вартості облігації цей ефект повинен по­значитися на курсовій вартості облігації.

Розглянемо тепер випадок короткострокових (трива­лістю один рік) облігацій, що більш характерно для еко­номіки України. Нехай номінальна вартість облігації стано­вить 100 гривень зі строком погашення через 364 дні. Процентні виплати проводяться через кожний 91 день у розмірі 25 гривень, причому останній купон виплачується в момент погашення облігації одночасно з номіналом. Нехай квартальна прибутковість аналогічних боргових зобов'язань (для орієнтира можна вибрати облігації внутрішньої держав­ної позики) становить 10%. Відповідно до формули (11.1) одержимо:

V_B = = 25 ∙ 3,1699 + 100 ∙ 0,6830 = 147,55 .

Якщо по закінченню одного кварталу процентна ставка драматично збільшилася до 18 відсотків, то вартість облігації складе:

V_B = = 25 ∙ 2,1743 + 100 ∙ 0,6086 = 115,22 .

Така зміна закономірна і відображає реальну ринкову си­туацію. Зокрема, якщо положення внаслідок сплеску інфляції ; різко погіршиться й квартальна процентна ставка складе 32%, то облігації будуть продаватися нижче свого номіналу.

V_B = = 25 ∙ 1,7663 + 100 ∙ 0,4348 = 87,64 .

Звернемося тепер до дисконтних облігацій, які також ма­ють номінальну вартість, що виплачується інвесторові в момент погашення облігації. У процесі емісії такі облігації продаються із знижкою (дисконтом). Величина знижки визначається про­центною ставкою по даній облігації. Подальше вивчення оцінки вартості такої облігації проведемо за допомогою кон­кретного приклада.

Приклад 2. Підприємство А в день емісії придбало за ціною 82 гривні за штуку пакет дисконтних державних облігацій з періодом обігу 365 днів і номінальною вартістю до погашення 100 гривень. Прибутковість цього фінансового інструмента на момент емісії становить:

K_d = = 21,95%

Через 165 днів, або за 200 днів до погашення облігації, підприємство А вирішило реалізувати на ринку цей пакет цінних паперів, тому що йому терміново знадобилися гроші. Ціна продажу була визначена в такий спосіб:

P₂ = = 89,26

Продавець дисконтував вартість облігації до погашення (100 гривень), використавши як дисконтну ставку (21.95%) той рівень прибутковості, що забезпечував йому даний фінансовий інструмент. Зміст цього розрахунку полягає в тому, щоб роз­ділити первісну величину дисконтного доходу (100 — 82 = 18 гривень) між продавцем і покупцем відповідно до тривалості періодів володіння фінансовим активом. Продавець володів активом 165 днів з 365, і він бажає одержати свою частину дис­контного доходу: 89.26 — 82 = 7.26 гривень із однієї облігації. Покупцеві (на думку продавця) повинна дістатися та частина дисконтного доходу, що відповідає 200 дням володіння фінан­совим інструментом:

100 − 89.26 = 10.74 гривні.

Інституціональні інвестори, що бажають придбати ці дер­жавні облігації, вважали запропоновану ціну завищеною, тому що домінуюча процентна ставка на ринку аналогічних фінан­сових ресурсів на момент продажу склала 23 відсотка. Оцінка вартості облігацій у цьому випадку становить:

P₂ = 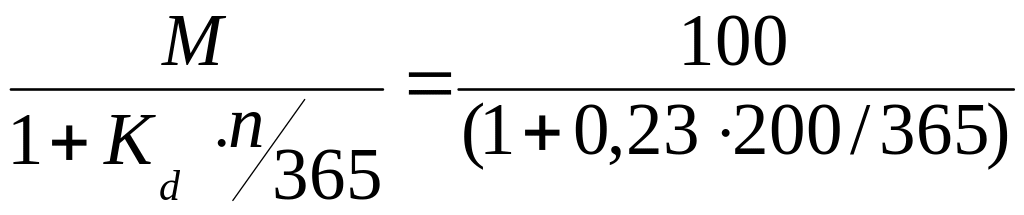= 88,81

тобто стала закономірно нижче. Підприємству А довелося за­довольнитися даною вартістю свого фінансового ресурсу.

Характеризуючи цей факт, сучасна фінансова теорія спра­ведливо називає минулі витрати "мертвими", тобто вони не мають значення при обґрунтуванні фінансових рішень.

Відповідно до прийнятих норм випуску звичайних акцій сума виплачуваних дивідендів залежить від результатів діяль­ності підприємства у відповідному періоді часу, зазвичай про­тягом року. Проте оцінка вартості звичайних акцій припускає деякий потік дивідендів, які при оцінці вартості відіграють та­ку ж роль, як процентні платежі при оцінці облігації. Тільки на відміну від облігацій цей потік нескінченний і не передба­чається повернення вихідної інвестиції. З урахуванням усього відзначеного вище оцінка вартості звичайної акції здійсню­ється за формулою:

P_s = , (11.15)

де: D_t — величина дивіденду, виплачуваного в t-тому році,

K_s — показник дисконту, за допомогою якого здійсню­ється приведення дивідендних виплат на цей момент часу.

Проблеми, пов'язані з оцінкою вартості акцій, полягають в прогнозі дивідендів й в оцінці показника дисконту. Розгляне­мо кожну з них окремо.

Зовсім очевидно, що підприємство не в змозі здійснити індивідуальний прогноз дивідендів на всьому нескінченному періоді. Тому на практиці цей період розбивають на дві части­ни, перша з яких становить кілька років (найчастіше не більше п'яти), протягом яких існує можливість скласти більш-менш правдоподібний прогноз дивідендних виплат. Друга частина — це весь нескінченний період, що залишився, час, для якого ро­биться припущення про те, що:

□ дивіденди зберігають незмінне значення, рівне величині останнього спрогнозованого дивіденду, що ввійшов у перший період, або

□ передбачається деякий постійний річний приріст дивідендів, обумовлений величиною процентного росту g. Надалі оцінка вартості акції — це справа техніки дискон­тування прогнозованої сукупності дивідендів.

Результуюча формула для оцінки вартості звичайних акцій може бути записана в такий спосіб:

P_s = P' + P'' ∙ , (11.16)

де Р'— дисконтне значення прогнозованих дивідендів на пер­шому (кінцевому) проміжку часу тривалістю N років;

Р''— дисконтне значення наступної нескінченної серії дивідендів, наведене до моменту часу, що відповідає кінцю N-ого року.

Для розрахунку першого компонента необхідно просто продисконтувати всі величини дивідендів, сплановані до ви­плати протягом перших N років:

P' = . (11.17)

Розрахунок другого компонента для незмінних дивідендів проводиться за формулою дисконтування нескінченних дивідендів

P'' = (11.18)

Якщо передбачається зростання дивідендів з темпом g, то необхідно скористатися формулою Гордона, що є узагальнен­ням формули (5.5) і має для розглянутого завдання такий вигляд:

P'' = 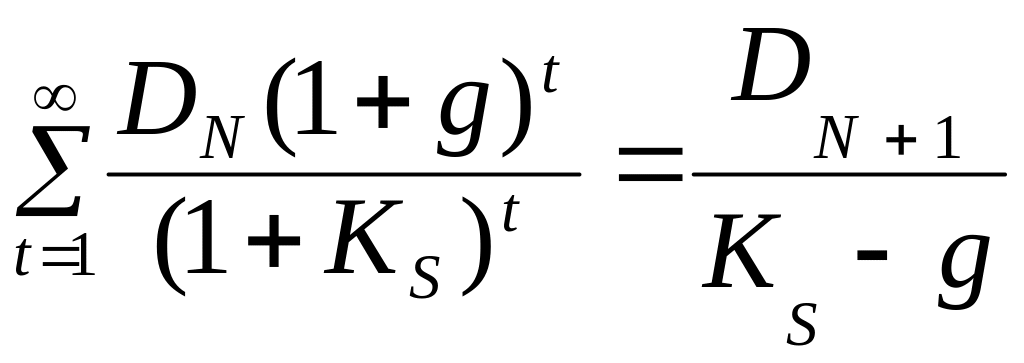. (11.19)

Завдання оцінки вартості звичайних акцій вирішується однозначно при відомому показнику дисконту. Для конкрет­ного підприємства він визначається з урахуванням ступеня ризикованості інвестування в це підприємство. Взаємозв'язок ризику й прибутковості інвестицій буде докладно розглянуто в наступній темі. Зараз же тільки відзначимо, що для визна­чення прибутковості акцій К_s потрібно мати порівняльні дані даного підприємства й фондового ринку в цілому. І природно потрібно мати цей фондовий ринок. У сучасних умовах Ук­раїни говорити про це, як про факт, що здійснився, поки ще ду­же рано, і тому доводиться використовувати більш спрощені й наближені підходи.

Один з таких підходів полягає в наступному. Як показник прибутковості K_s використовується оцінка прибутковості підприємства, спостережувана протягом останнього року. Ця прибутковість визначається за допомогою двох компонентів:

□ дохідності інвестора, одержуваної у вигляді дивідендів (величина дивіденду, виплачена за останній рік, поділе­на на ринкову вартість акції);

□ прибутковість інвестора, пов'язана зі збільшенням кур­сової вартості акції (збільшення курсової вартості акції за рік, поділене на курсову вартість на початку року).

Склавши наведені вище компоненти, ми одержимо при­бутковість акції.

У процесі розробки інвестиційних проектів можуть залу­чатися кредитні ресурси, які повертаються в процесі реалізації проекту. Сума кредиту зазвичай повертається поступово про­тягом його строку. Розрізняють два типи порядку погашення:

□ періодичними внесками ("повітряна куля");

□ "амортизаційний" (поступова виплата рівномірними внесками).

Погашення періодичними внесками. При цьому способі основну суму кредиту виплачують протягом усього строку кредиту. Однак порядок погашення такий, що по закінченні строку від суми кредиту залишається досить значна частка, що підлягає погашенню.

Приклад 3. Уявимо собі, що підприємство одержує кредит у сумі 100,000 грн строком на 5 років. Платежі в рахунок пога­шення кредиту вносяться щорічно в сумі 12,000 грн плюс відсоток. Таким чином, наприкінці 5-річного періоду уже здійснені чотири платежі по 12,000 грн (усього 48,000 грн), і залишається невиплаченою сума в 52,000 грн, яку повністю виплачують по закінченні строку кредиту. Такий порядок по­гашення проілюстрований у табл. 11.2.

Зазначимо, що відсотки нараховуються, виходячи з вели­чини початкового на поточний рік балансу боргу.

Кредит може бути погашений рівними внесками. Відсоток виплачують по непогашеній частині боргу, тому загальна сума внеску по погашенню основної суми й відсотка зменшується в міру того, як минає строк кредиту. Внески по погашенню ос­новної суми не змінюються. Однак кожна наступна процентна виплата менше попередньої, тому що непогашена частина, що залишається від основної суми зменшується.

Таблиця 11.2