5.3. Магнитные моменты электронов и атомов

Магнитные свойства вещества, в конечном счете, обусловлены магнитными свойствами составляющих его частиц. Исследования показали, что магнитные моменты протонов и нейтронов малы по сравнению с магнитными моментами электронов. Следовательно, магнитные свойства атома целиком определяются электронами.

Всякий атом можно рассматривать как динамическую систему, состоящую из ядра и движущихся вокруг его электронов.

Будем считать, что электроны в атомах движутся по круговым орбитам. Движение электрона по замкнутой орбите представляет собой ток. Направление тока противоположно движению электрона (рис.5.4).

Пусть – угловая скорость вращения электрона. Вектор угловой скорости образует с направлением движения электрона правовинтовую систему.

Величина орбитального тока равна

. (5.14)

Ему соответствует орбитальный магнитный момент электрона

. (5.15)

Магнитный момент образует с создающим его током правовинтовую систему и направлен противоположно вектору угловой скорости:

, . (5.16)

Движущийся по орбите электрон обладает моментом импульса:

. (5.17)

Вектор называется орбитальным механическим моментом электрона, его направление совпадает с направлением вектора угловой скорости: .

Векторы и жестко связаны и противоположны по направлению: .

Отношение магнитного момента частицы к ее механическому моменту называется гиромагнитным отношением. Найдем гиромагнитное отношение орбитальных моментов электрона.

. (5.18)

Формула (5.18) не содержит параметров орбиты электрона. Следовательно, гиромагнитное отношение одинаково для всех электронных орбит.

Независимо от орбитального движения электрон обладает собственным механическим и магнитными моментами. Обозначим их и . Собственный момент импульса электрона называется спином^.

Гиромагнитное отношение спиновых моментов электрона оказалось равным

. (5.19)

Полный магнитный момент атома представляет собой векторную сумму орбитальных и спиновых магнитных моментов электронов. Пусть в состав атома входит z электронов. Тогда магнитный момент атома равен:

. (5.20)

Первое слагаемое в этом выражении представляет собой векторную сумму орбитальных магнитных моментов, второе - спиновых магнитных моментов электронов атома.

5.4. Влияние магнитного поля на орбитальное движение электронов. Объяснение диамагнетизма

Рассмотрим, какие изменения произойдут в орбитальном движении электрона при наложении внешнего магнитного поля.

Пусть плоскость орбиты ориентирована произвольно относительно внешнего магнитного поля, и орбитальный магнитный момент электрона составляет с вектором некоторый угол . На замкнутый ток в магнитном поле действует момент силы

. (5.21)

Под действием этого момента силы орбита электрона будет поворачиваться так, что угол между векторами и остается постоянным (рис.5.5). Вектор орбитального магнитного момента электрона будет описывать «конус» вокруг направления внешнего магнитного поля. Такое движение электронной орбиты называется прецессией.

Задача о прецессии электронных орбит во внешнем магнитном поле была решена Лармором. Для угловой скорости прецессии получено выражение

. (5.22)

Величину называют частотой или угловой скоростью Лармора.

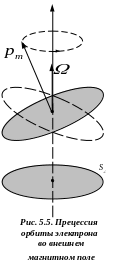Рассмотрим основные выводы теоремы Лармора.

Действие внешнего магнитного поля на движущийся по орбите электрон заключается в следующем.

• На первоначальное движение электрона накладывается дополнительное вращение вокруг направления магнитного поля с угловой скоростью Лармора .

• Вектор угловой скорости Лармора параллелен внешнему полю:

• Угловая скорость Лармора не зависит от параметров электронной орбиты и от ее ориентации и одинакова для всех электронов атома.

Дополнительному вращению электрона с угловой скоростью соответствует дополнительный орбитальный ток и дополнительный индуцированный полем магнитный момент электрона, равный по величине

. (5.23)

Здесь - площадь проекции орбиты на плоскость, перпендикулярную полю (рис.5.5).

Вектор направлен противоположно вектору угловой скорости , поэтому выражение (5.23) в векторной форме будет иметь вид:

. (5.24)

Подставим в формулу (5.24) выражение для из (5.22), получим:

. (5.25)

Индуцированный внешним магнитным полем дополнительный магнитный момент электрона направлен противоположно полю.

Пусть атом содержит Z электронов, тогда индуцированный магнитный момент атома равен:

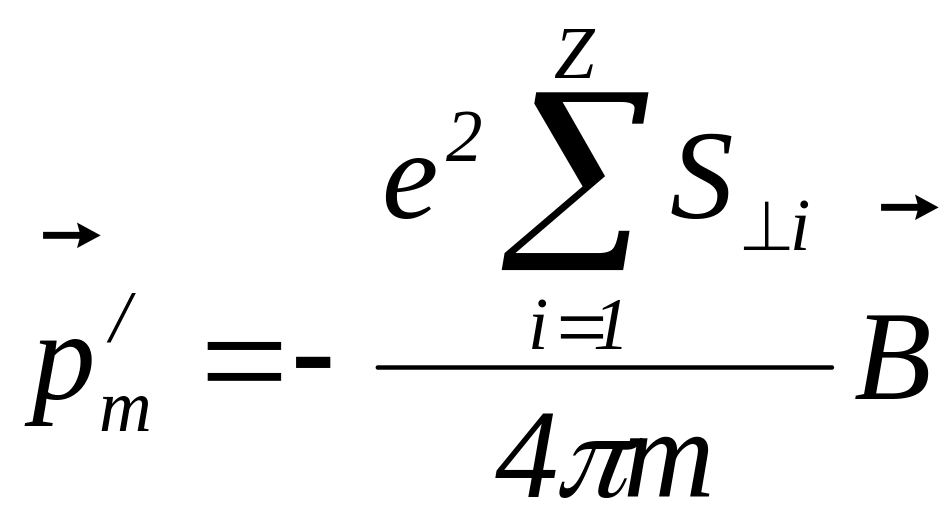. (5.26)

Свойство атомных электронов создавать дополнительный магнитный момент, направленный противоположно внешнему полю, называется диамагнетизмом.

Поскольку орбитальное движение электронов свойственно всем атомам и молекулам, то диамагнитный эффект имеет место во всех веществах без исключения. Но обнаруживается он лишь у тех веществ, атомы и молекулы которых не обладают магнитным моментом.

Если суммарный магнитный момент атома или молекулы (в отсутствие внешнего поля) равен нулю, то вещество проявляет диамагнитные свойства, то есть является диамагнетиком.

Если суммарный магнитный момент атома или молекулы (в отсутствие внешнего поля) не равен нулю, то диамагнитный эффект будет маскироваться более сильным парамагнитным эффектом.