
Розв’язання






Відповідь: ________________________
Знайти загальні розв’язки рівнянь
Довгострокові завдання
Розв’язати однорідні рівняння:





 якщо
якщо

 якщо
якщо
























Заняття №4
Тема. Рівняння в повних диференціалах (2 год.)
Теоретичний блок
Рівняння
першого порядку, які є розв’язаними
відносно похідної
 завжди
можна записати у диференціальній формі:
завжди
можна записати у диференціальній формі:

Помноживши
на
 можна
дане рівняння переписати у більш
симетричній формі:
можна
дане рівняння переписати у більш
симетричній формі:


 .
.
У деяких випадках рівність (1) є повним диференціалом деякої функції:



Необхідною і достатньою умовою існування повного диференціала є рівність мішаних похідних другого порядку:

Отже, для того, щоб диференціальне рівняння було рівнянням у повних диференціалах необхідно і достатньо, щоб виконувалась умова:

В загальному існує два зручних методів знаходження загального розв’язку диференціального рівняння:
безпосереднє інтегрування;
використовуючи значення частинних похідних функції .
Приклад. Розв’язати рівняння:


Перевіримо умову повного диференціалу:
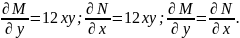
Отже, маємо рівняння в повних диференціалах.
І спосіб. Інтегруємо праву і ліву частину рівняння:

Даний інтеграл є криволінійним інтегралом ІІ-го роду. Із курсу математичного аналізу відомо, що при умові повного диференціала значенні інтеграла не залежить від шляху інтегрування.
Очевидно,
найзручнішим шляхом інтегрування є
інтегрування вздовж ділянок ламаної,
які паралельні вісі
 відповідно (рис. 1).
відповідно (рис. 1).



Рис. 1
Так як підінтегральні функції не мають особливих точок, то інтегрування проведемо вздовж ламаної:




ІІ спосіб.
І випадок:




ІІ випадок:













Практичний блок
Дано розв’язок рівняння в повних диференціалах. Заповніть пропуски.
 (рівняння
розв’язане методом безпосереднього
інтегрування).
(рівняння
розв’язане методом безпосереднього
інтегрування).
Розв’язання



Інтегруємо
вздовж ламаної
 (рис. 1):
(рис. 1):


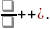
Відповідь: __________________________
2) (рівняння
розв’язане методом безпосереднього
інтегрування).
(рівняння
розв’язане методом безпосереднього
інтегрування).
Розв’язання



Інтегруємо вздовж ламаної (рис. 1):

Відповідь:__________________________
3) (рівняння
розв’язане з використанням значення
частинних похідних функції
).
(рівняння
розв’язане з використанням значення
частинних похідних функції
).
Розв’язання









Відповідь:__________________________
4)
 (рівняння
розв’язане з використанням значення
частинних похідних функції
).
(рівняння
розв’язане з використанням значення
частинних похідних функції
).
Розв’язання








Відповідь:__________________________
Перевірити, що дані рівняння є рівняннями в повних диференціалах і розв’язати їх:
__________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
__________________________________________________________________
Відповідь:__________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Відповідь:__________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Відповідь:__________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
Відповідь:__________________________
Блок завдань для самостійного опрацювання
Дано розв’язок рівняння в повних диференціалах. Заповніть пропуски.







