
ЗМІСТ
Заняття №1. Диференціальні рівняння першого порядку з
відокремлюваними змінними…………………………………………………….6
Заняття №2. Метод Лагранжа та Бернулі розв’язування
лінійних диференціальних рівнянь першого порядку………………………...14
Заняття №3. Однорідні диференціальні рівняння та рівняння,
що зводяться до них……………………………………………………………..22
Заняття №4. Рівняння в повних диференціалах……………………………….29
Самостійна робота №1…………………………………………………………..37
Заняття №5. Інтегруючий множник…………………………………………….39
Заняття №6. Рівняння першого порядку n-го степеня………………………...47
Заняття №7. Загальний метод введення параметризації.
Рівняння Лагранжа і Клеро……………………………………………………...55
Контрольна робота №1………………………………………………………….63
Відповіді………………………………………………………………………….67
Література………………………………………………………………………..78
Заняття №1
Тема. Диференціальні рівняння першого порядку з відокремлюваними змінними (2 год.)
Теоретичний блок
Диференціальним рівнянням називається рівняння, яке пов'язує між собою незалежну змінну х, шукану функцію у та її похідні або диференціали.
Символічно диференціальні рівняння записуються так:



Диференціальне рівняння називається звичайним, якщо шукана функція залежить від однієї незалежної змінної.
Порядком диференціальною рівняння називається найвищий порядок похідної або диференціала невідомої функції в даному рівнянні.
Розв'язком (або інтегралом) диференціального рівняння називається така функція, яка перетворює це рівняння в тотожність.
Загальним розв'язком (або загальним інтегралом) диференціального рівняння називається такий розв'язок, до якого входить стільки незалежних довільних сталих, який порядок рівняння. Так, загальний розв'язок диференціального рівняння першого порядку має одну довільну сталу.
Частинним розв'язком диференціального рівняння називається розв'язок, знайдений із загального при різних числових значеннях довільних сталих. Значення довільних сталих знаходять при певних початкових значеннях аргументу і функції.
Графік частинного розв'язку диференціального рівняння називається інтегральною кривою. Загальному розв'язку диференціального рівняння відповідає сукупність (сім'я) всіх інтегральних кривих.
Диференціальним рівнянням першого порядку називається рівняння, до якого входять похідні (або диференціали), не вищі першого порядку.
Диференціальним рівнянням з відокремлюваними змінними називається рівняння виду

Щоб розв'язати це рівняння, треба спочатку відокремити змінні:

а потім проінтегрувати обидві частини знайденої рівності:

Приклад 1. Знайти загальний розв’язок рівняння

Відокремивши змінні маємо:

Інтегруємо обидві частини цього рівняння:



Оскільки довільна стала С може набувати будь-яких числових значень,
тому
для зручності наступних перетворень
замість С
ми написали
 lnC.
lnC.
Потенціюючи останню рівність, дістанемо:

Приклад 2. Знайти частинний розв’язок рівняння

якщо
y

Відокремлюємо змінні:

Проінтегрувавши обидві частини рівняння, отримаємо:





 – загальний
розв’язок даного рівняння.
– загальний
розв’язок даного рівняння.
Знайдемо
значення С,
для цього підставимо
 та
та
 у загальний розв’язок:
у загальний розв’язок:



Отже,

 частинний розв’язок, який задовольняє
початкові умови.
частинний розв’язок, який задовольняє
початкові умови.
Практичний блок
Дано розв’язок диференціального рівняння з відокремлюваними змінними. Заповніть пропуски.
Розв’язання

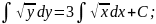


Відповідь: ________________________
Розв’язання





Відповідь: ________________________
Розв’язання


Введемо заміну:


arcsin
 =
=
 2
2 +C
+C
arcsin
= C
 .
.
Відповідь: ________________________
Розв’язання




Відповідь: ________________________
 якщо
якщо

Розв’язання

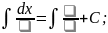






Відповідь: ________________________
 ,
якщо
,
якщо

Розв’язання




Відповідь: ________________________
Знайти загальні розв’язки рівнянь:
 ;
;
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
 ;
;
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
Блок завдань для самостійного опрацювання
Дано розв’язок диференціального рівняння з відокремлюваними змінними. Заповніть пропуски.

Розв’язання


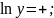





Відповідь:________________________
Знайти частинні розв’язки рівнянь:
 якщо
якщо

 якщо
якщо

 якщо
якщо

Довгострокові завдання
Знайти розв’язок рівняння:





















 ,
якщо
,
якщо









Заняття №2
Тема. Метод Лагранжа та Бернулі розв’язування лінійних диференціальних рівнянь першого порядку (2 год.)
Теоретичний блок
Диференціальне рівняння називається лінійним, якщо воно є лінійним відносно шуканої функції та похідних відносно шуканої функції.
Лінійне диференціальне рівняння першого порядку має вигляд
 (1)
(1)
де
 і
і
 – відомі задані функції.
– відомі задані функції.
Рівняння
(1) є неоднорідним лінійним рівнянням.
Якщо
 ,
то рівняння (1) називається однорідним
лінійним диференціальним рівнянням.
,
то рівняння (1) називається однорідним
лінійним диференціальним рівнянням.
Однорідне лінійне рівняння завжди дозволяє відокремлення змінних.


 загальний
розв’язок однорідного лінійного
рівняння.
загальний
розв’язок однорідного лінійного
рівняння.
Одним із методів, яким можна розв’язати рівняння (1) є метод варіації довільно сталої (метод Лагранжа).
Ідея
методу у тому, що загальний розв’язок
рівняння (1) шукають у формі загального
розв’язку відповідного однорідного
лінійного рівняння, де в якості сталої
 є деяка функція
є деяка функція
 ,
яку підбирають так, щоб виконувалось
рівняння (1).
,
яку підбирають так, щоб виконувалось
рівняння (1).

Для знаходження підставимо шукану форму розв’язку в рівняння (1).



Розкривши дужки, отримаємо:

Загальний розв’язок рівняння (1), як видно з останнього запису складається з двох доданків, перший з яких є загальним розв’язком відповідного однорідного рівняння, а другий доданок є частинним розв’язком.
Розв’язати
лінійне диференціальне рівняння першого
порядку можна іншим методом (методом
Бернулі), якщо шукану функцію
 зобразити у вигляді добутку двох
невідомих функцій:
зобразити у вигляді добутку двох
невідомих функцій:

Маємо однорідне рівняння, розв’язок якого є:

Далі все відбувається аналогічно, як у методі варіації довільної сталої.
Приклад 1. Розв’язати лінійне диференціальне рівняння методом Лагранжа:










Приклад 2. Розв’язати лінійне диференціальне рівняння методом Бернулі:

Це
лінійне рівняння, тут
 Припустимо,
що
Припустимо,
що
 Продиференціюємо
цю рівність по
Продиференціюємо
цю рівність по
 :
:

Підставивши
тепер вирази для
та
 у
дане рівняння, дістанемо:
у
дане рівняння, дістанемо:

 (1)
(1)
Оскільки
одну із допоміжних функцій
 або
або
 можна
взяти довільно, то за
візьмемо
один з частинних розв’язків рівняння
можна
взяти довільно, то за
візьмемо
один з частинних розв’язків рівняння

Відокремивши в цьому рівняння змінні та інтегруючи, отримаємо:


Вважаємо,
що довільна стала
 бо знаходимо один з частинних розв’язків.
бо знаходимо один з частинних розв’язків.
Підставимо тепер вираз для в рівняння (1) і дістанемо рівняння:

Тоді:

Знаючи і , отримаємо тепер загальний розв’язок даного рівняння:

Практичний блок
Дано розв’язки лінійних диференціальних рівнянь (№1, 2 розв’язані методом Лагранжа, №3, 4 – методом Бернулі). Заповніть пропуски.
Розв’язання






Відповідь: __________________________
Розв’язання






Відповідь: _________________________
Розв’язання







ln





Відповідь: __________________________
Розв’язання

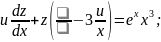






Відповідь: __________________________
Знайти загальні розв’язки рівнянь (рівняння №1, 2 розв’язати методом Лагранжа, №3, 4 – методом Бернулі):
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
 −
−
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Відповідь:__________________________
Блок завдань для самостійного опрацювання
Дано лінійне диференціальне рівняння, розв’язане методом Лагранжа. Заповніть пропуски.
















