11

Министерство образования и науки Украины

Севастопольский национальный технический университет

ИССЛЕДОВАНИЕ

АВТОМАТИЧЕСКИХ СИСТЕМ КОМБИНИРОВАННОГО

УПРАВЛЕНИЯ

Методические указания

к выполнению лабораторной работы по дисциплине

«Теория автоматического управления»

для студентов дневной и заочной формы обучения

направления подготовки 6.0914

«Компьютеризированные системы, автоматика и управление»

Севастополь

2004

УДК 681.5

Исследование автоматических систем комбинированного управления: Методические указания к выполнению лабораторной работы по дисциплине «Теория автоматического управления»/Сост. А.И.Грушун.- Севастополь: Изд-во СевНТУ, 2004.- с.

В методических указаниях рассматриваются и исследуются вопросы компенсации внешних воздействий в системах автоматического управления с помощью комбинированного управления.

Методические указания предназначены для студентов дневной и заочной форм обучения направления подготовки 6.0914 «Компьютеризированные системы, автоматика и управление».

Методические указания рассмотрены и утверждены на заседании кафедры технической кибернетики СевНТУ (протокол № 5 от 3 февраля 2004 г.).

Допущено учебно-методическим центром СевНТУ в качестве методических указаний.

Рецензент: Крамарь В.А., канд. техн. наук, доцент.

Содержание

1. Цель работы 3

2. Краткие теоретические сведения 3

3. Описание технических средств выполнения работы 3

4. Порядок выполнения теоретических расчетов 3

5. Порядок выполнения экспериментальных исследований 6

6. Содержание отчета о выполнении лабораторной работы 7

7. Контрольные вопросы 7

Библиографический список 8

1. Цель работы

Исследование влияния компенсирующих цепей на статические и динамические характеристики системы автоматического управления (САУ) скорости вращения вала двигателя постоянного тока.

2. Краткие теоретические сведения

Часто одной обратной связи оказывается недостаточно для обеспечения нужной точности системы, испытывающей различные возмущения. Выход состоит в применении идей управления с обратной связью в сочетании с принципом компенсации внешних воздействий [1, 2]. В этом случае управляющий сигнал в САУ имеет две составляющие. Одна формируется с помощью зарегистрированной ошибки управления, а вторая формируется так, чтобы компенсировать вредное воздействие некоторого возмущения непосредственно без измерения ошибки.

Пусть в САУ введена цепь реагирования на возмущающее воздействие. Часть прямой цепи такой системы можно представить схемой, изображенной на рисунке 1.

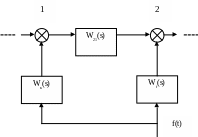
Рисунок 1 – Фрагмент прямой цепи САУ с цепью компенсации возмущения

На рисунке 1 f(t) – неизвестное как функция времени возмущающее воздействие; W_f(s) – передаточная функция цепи входа возмущающего воздействия в прямую цепь САУ; W₂₁(s) – передаточная функция фрагмента прямой цепи САУ; W_к(s) - передаточная функция цепи компенсации возмущения.

Для выбора W_к(s) изобразим схему (рисунок 2), эквивалентную изображенной на рисунке 1.

Рисунок 2 - Эквивалентная структурная схема САУ с компенсацией возмущения

На рисунке 2 f_э(s)= [W_f(s)+W_к(s)W₂₁(s)]f(s). Тогда условие полной (абсолютной) компенсации будет иметь вид:

f_э(s)0  W_f(s)+ W_к(s) W₂₁(s)0

или

W_к(s)= -W_f(s)/ W₂₁(s). (1)

Если W_к(s) оказывается физически реализуемой, то есть степень знаменателя этой функции не меньше степени числителя, то мы достигаем эффекта полной компенсации. Это значит, что каким бы ни было воздействие f(t) выход системы на него не реагирует, а, следовательно, и составляющие ошибки этого воздействия равны нулю. Такие системы принято называть полностью или абсолютно инвариантными.

Если функция (1) не относится к классу физически возможных, то полная компенсация, а, следовательно, инвариантность не достигается. В этом случае говорят об «инвариантности до ошибки _i» или неполной компенсации.

Можно показать, что (t)0 при t для определенных классов воздействий при выборе соответствующей W_к(s). Эффект неполной компенсации (частичной инвариантности) состоит в том, что путем выбора передаточной функции W_к(s) можно получать равными нулю коэффициенты ошибки С₀, С₁, С₂ и т.д.

Рассмотрим полную схему САУ с цепью компенсации (рисунок 3).

Рисунок 3 – Структурная схема САУ с компенсирующей цепью

Запишем выражение для ошибки от возмущающего воздействия:

Эта формула записана в предположении, что W_k(s) - произвольная передаточная функция. Рассмотрим как ее выбрать, чтобы обратить в ноль коэффициенты ошибки.

Пусть все звенья САУ статического типа. Определим передаточную функцию компенсирующего устройства W_k(s) из условия частичной инвариантности – равенства нулю статической ошибки по возмущению. Для этого необходимо выполнение условия C₀=0. Известно [1,2], что . Тогда справедлива запись . Следовательно, коэффициент, обеспечивающий компенсацию статической ошибки, можно записать в виде:

.

Если назначить передаточную функцию цепи компенсации в виде:

,

то за счет выбора коэффициентов k₁ и k₂ можно обратить в ноль коэффициенты статической и скоростной ошибки соответственно.

Известно [1,2], что установившуюся ошибку можно представить рядом

(s)=C₀f(s)+C₁Sf(s)+C₂S²f(s)+… =(C₀+ C₁S+C₂S²+…)f(s).

Если передаточную функцию замкнутой системы по ошибке от возмущения f(t) записать в виде

,

то условие частичной компенсации будет выглядеть следующим образом:

C₀=a₀(k₁)=0,

C₁=a₁(k₂)=0,

откуда легко получить коэффициенты k₁ и k₂ компенсации статической и скоростной ошибки.

Еще более усложняя передаточную функцию W_k(s), можно и далее коэффициенты установившейся ошибки обращать в ноль.