5. Однорідні системи лінійних алгебраїчних рівнянь
Означення. Система лінійних алгебраїчних рівнянь, в якій всі вільні члени дорівнюють 0 називається однорідною системою лінійних алгебраїчних рівнянь (ОСЛАР).
Загальний вигляд однорідної системи лінійних алгебраїчних рівнянь такий:
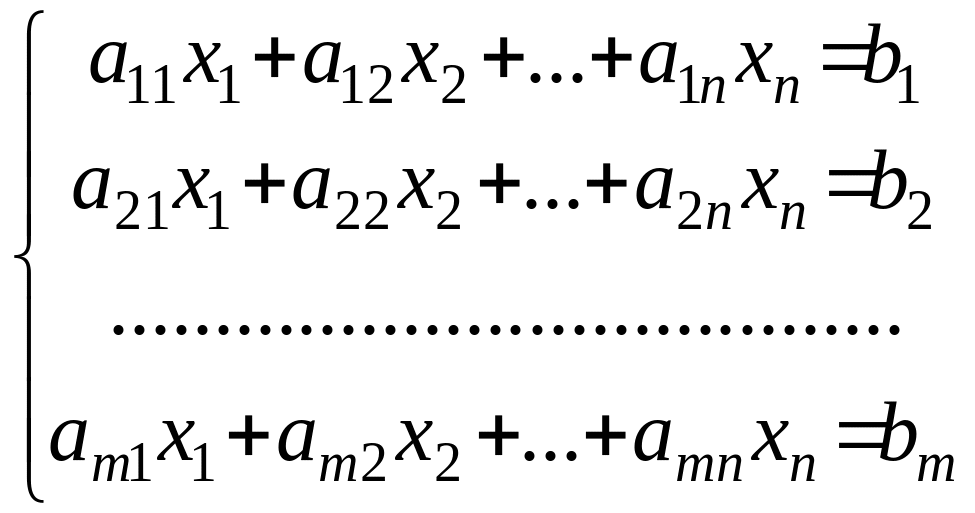(3)
Однорідна система лінійних алгебраїчних рівнянь завжди сумісна, тому що для всіх , і коефіцієнтів вона має розв’язок 0, 0,..., 0.Цей розв’язок називається нульовим або тривіальним. Будь-який розв’язок однорідної СЛАР, відмінний від нульового, називається ненульовим або нетривіальним.
Теорема (необхідна і достатня ознака сумісності ОСЛАР (3) ). Для того, щоб однорідна система лінійних алгебраїчних рівнянь (3) була сумісною, тобто мала нетривіальні розв’язки, необхідно і достатньо, щоб ранг матриці системи був менший числа невідомих.
Ослар (3) сумісна (має ненульові розв’язки)
Наслідок. Однорідна система лінійних алгебраїчних рівнянь, в якій число рівнянь дорівнює числу невідомих має ненульові розв’язки тоді і тільки тоді, коли її визначник дорівнює нулю.
Дійсно,
рівність
означає, означає, що ранг матриці системи
менше
.
Розв’язки однорідної системи лінійних алгебраїчних рівнянь мають наступні властивості.
1) Якщо
набір
є розв’язком системи (3), то для будь-якого
числа
набір
також буде розв’язком системи (3).
2) Якщо
набори
і
є розв’язками системи (3), то набір
+
також буде розв’язком системи (3).
3) Якщо
набори
є розв’язками системи (3), то набір
,
де
також
буде розв’язком системи (3).
Нехай однорідна система (3) невизначена, тобто має безліч розв’язків. Кожен її розв’язок – це деякий набір чисел, всі розв’язки утворюють нескінченну множину наборів чисел.
Теорема.
(про структуру розв’язків ОСЛАР).
Всі розв’язки однорідної система
лінійних алгебраїчних рівнянь можна
записати у вигляді
,
де
- число невідомих,
- ранг матриці системи,
.
Набір
розв’язків
,
про який йдеться в останній теоремі
називається базисною
системою
розв’язків.
Запис
= ,
називається загальним розв’язком ОСЛАР. Таким чином, загальний розв’язок ОСЛАР являє собою матрицю-рядок .
З теорем випливає наступна
Схема дослідження однорідної системи
1. Дослідимо систему на сумісність, для чого визначимо ранг матриці системи. У випадку сумісності:
2. Визначимо число вільних і базисних невідомих.
3. Виразимо базисні невідомі через вільні. Для цього застосуємо метод
Гаусса до матриці системи.
4. Знаходимо загальний розв’язок системи.
Приклад 1. Дослідити на сумісність, у випадку сумісності знайти розв’язки однорідної системи лінійних алгебраїчних рівнянь.
Розв’язання. 1) Дослідимо систему на сумісність, для чого визначимо ранг матриці системи:
~
,
отже система сумісна.
2) Визначимо число вільних і базисних невідомих.
,
,
– є одне вільне невідоме, наприклад,
.
Невідомі
і
– базисні.
3) Виразимо базисні невідомі через вільні. Для цього застосуємо метод Гаусса до матриці системи:
~
,
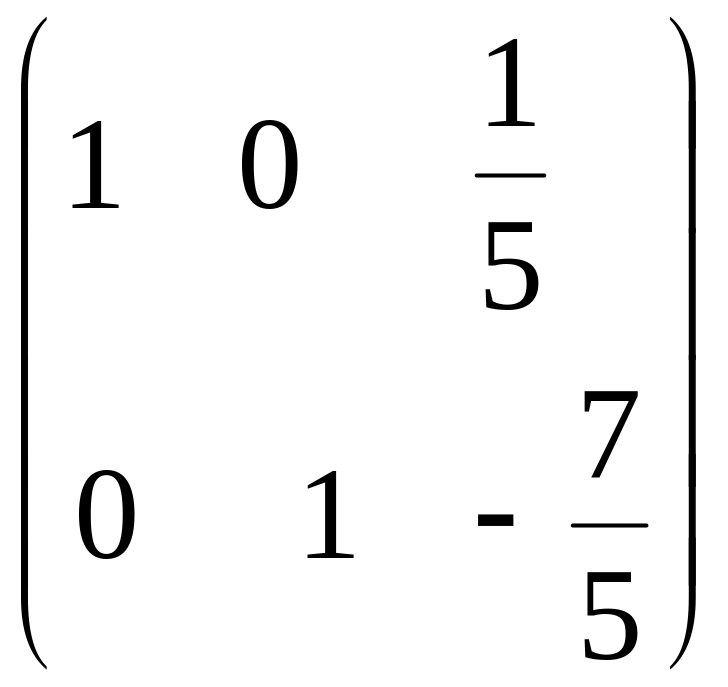звідки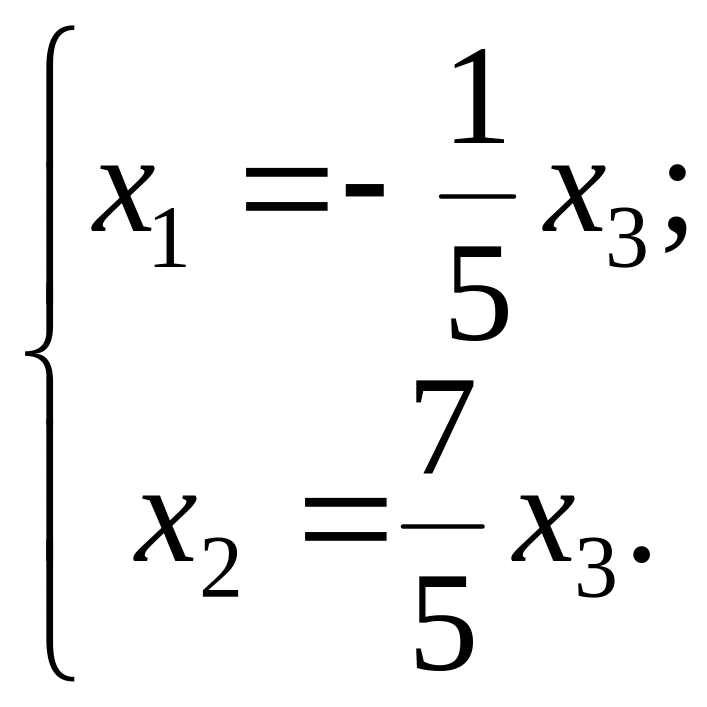 
4)
Знаходимо загальний розв’язок системи.
Вільним невідомим можна надавати
будь-яких значень. Нехай
,
де
.
Тоді
,
.
Загальний розв’язок: , , ,
Загальний розв’язок можна також записати у вигляді матриці-рядка
,
де
.
Відповідь: , де .
Приклад 2. Дослідити на сумісність, у випадку сумісності знайти розв’язки однорідної системи лінійних алгебраїчних рівнянь.
Розв’язання. 1) Дослідимо систему на сумісність, для чого визначимо ранг матриці системи:
~
~
~
~
.
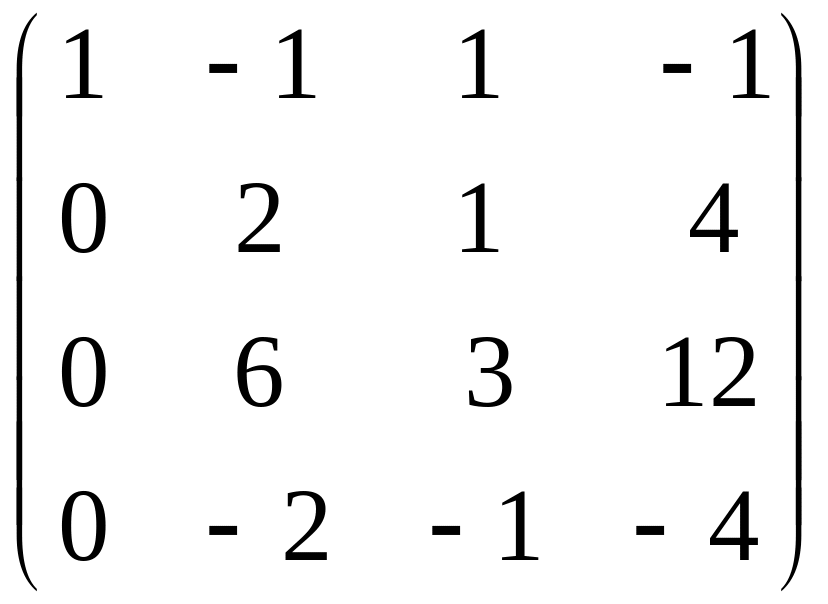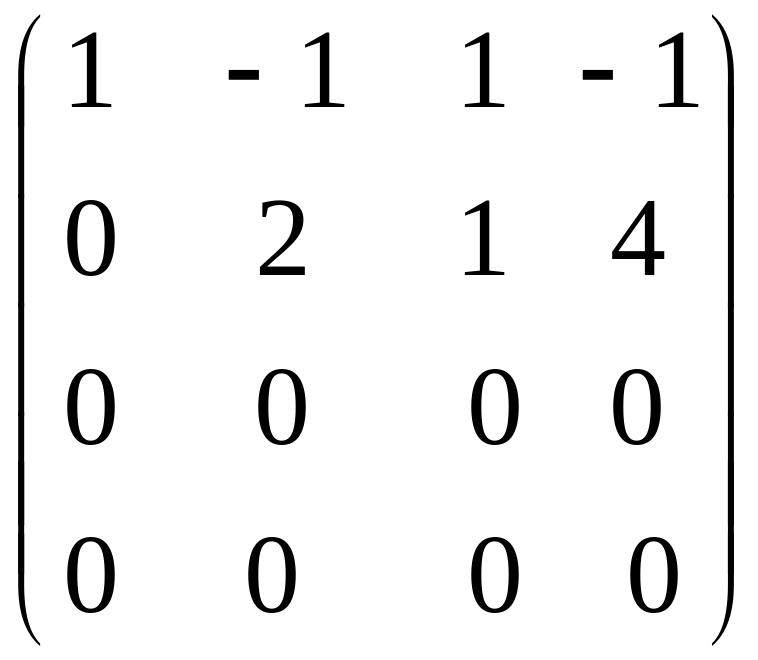Оскільки
,
то система сумісна.
Зауваження. Дослідити на сумісність можна обчисленням визначника. Очевидно, що він дорівнює 0.
2) Визначимо число вільних і базисних невідомих.
,
,
– є два вільних невідомих:
і
.
Невідомі і – базисні.
3) Виразимо базисні невідомі через вільні. Для цього застосуємо метод Гаусса до матриці системи:
~
~
,
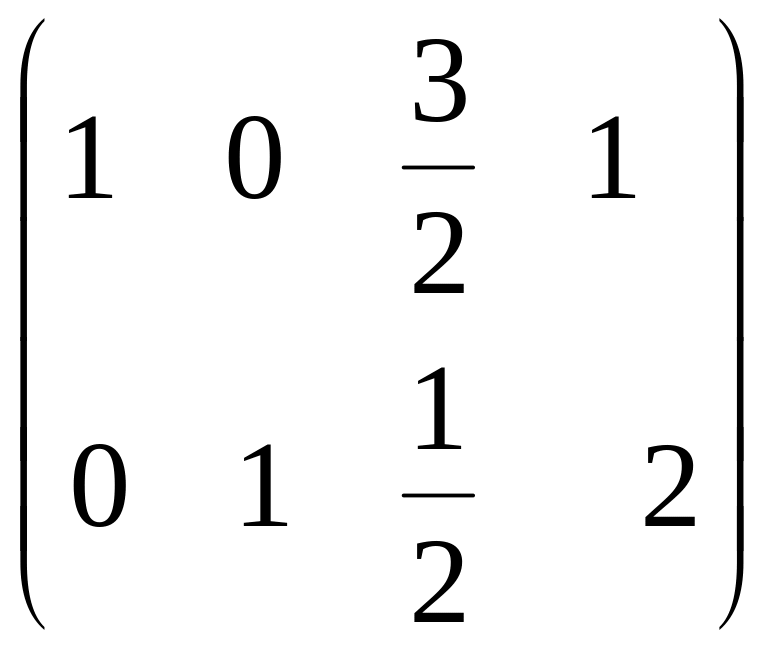звідки
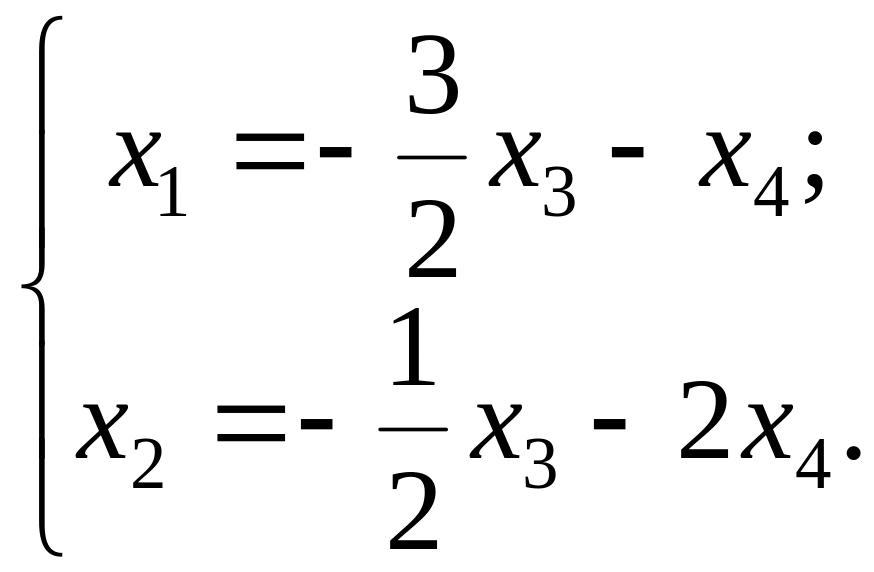
4)
Знаходимо загальний розв’язок системи.
Вільним невідомим можна надавати
будь-яких значень. Нехай
,
,
де
.
Тоді
,
,
,
або
,
,
,
.
Запишемо загальний розв’язок у вигляді матриці-рядка
,
де
.
Відповідь: , де .